圆幂定理专题教育课件市公开课一等奖百校联赛获奖课件.pptx

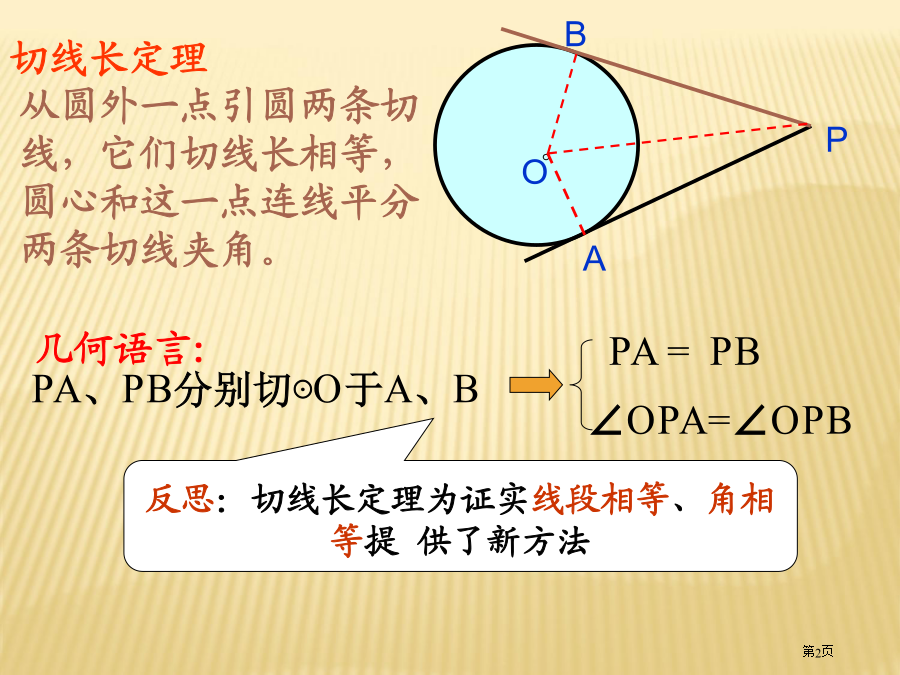
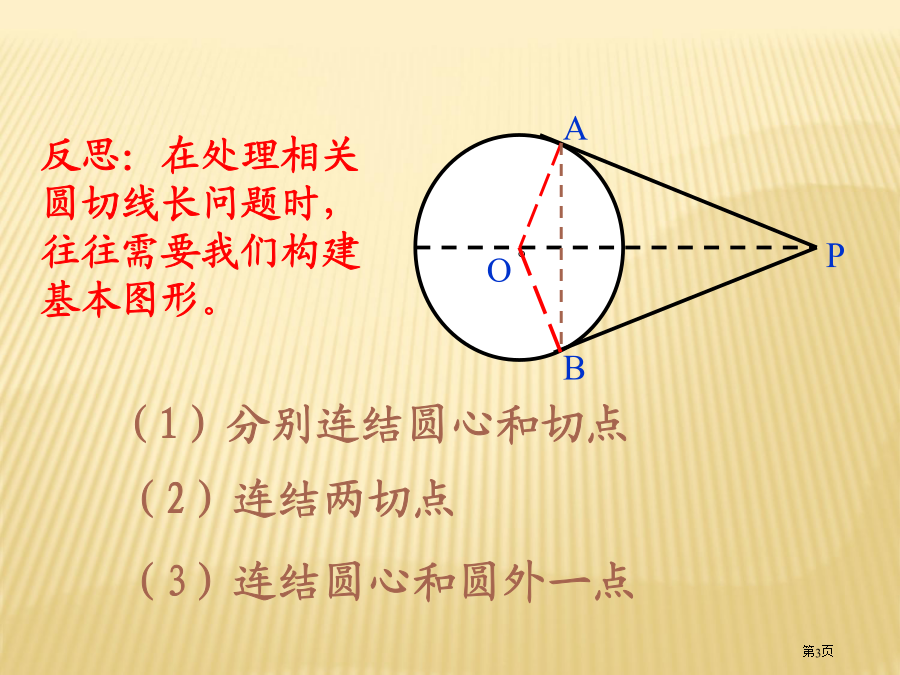
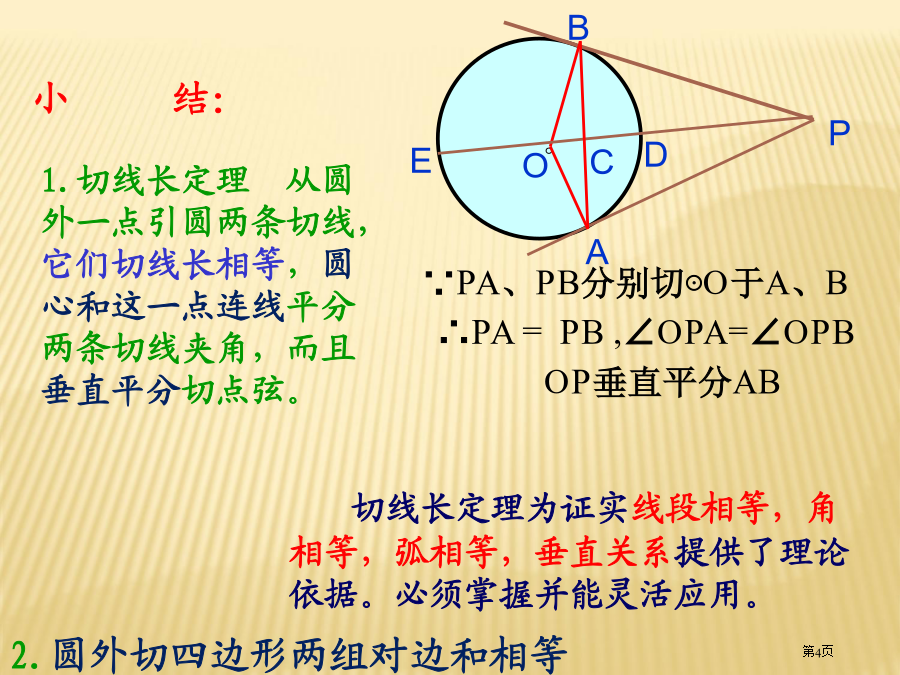
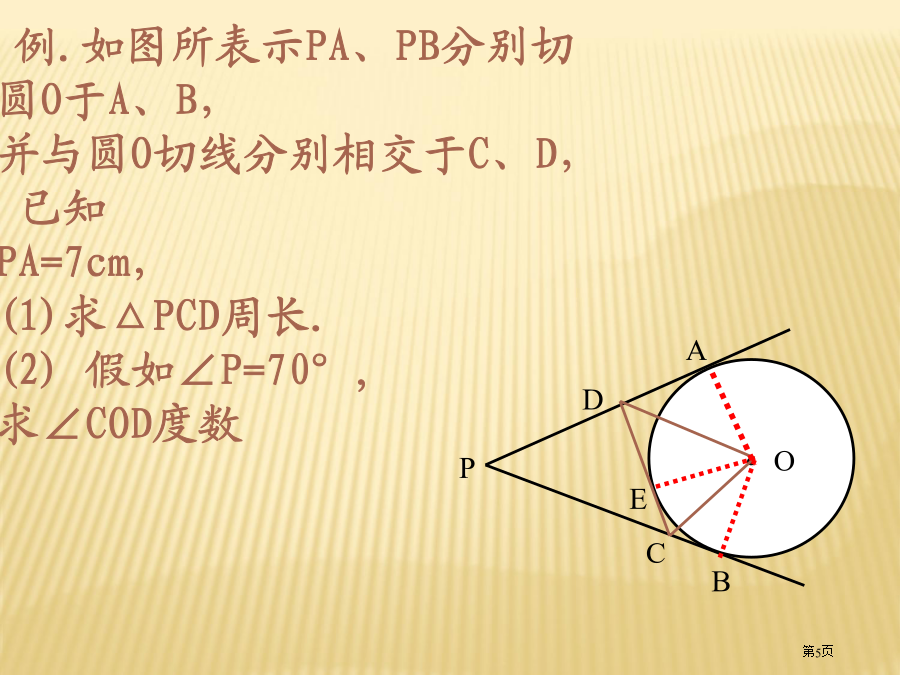
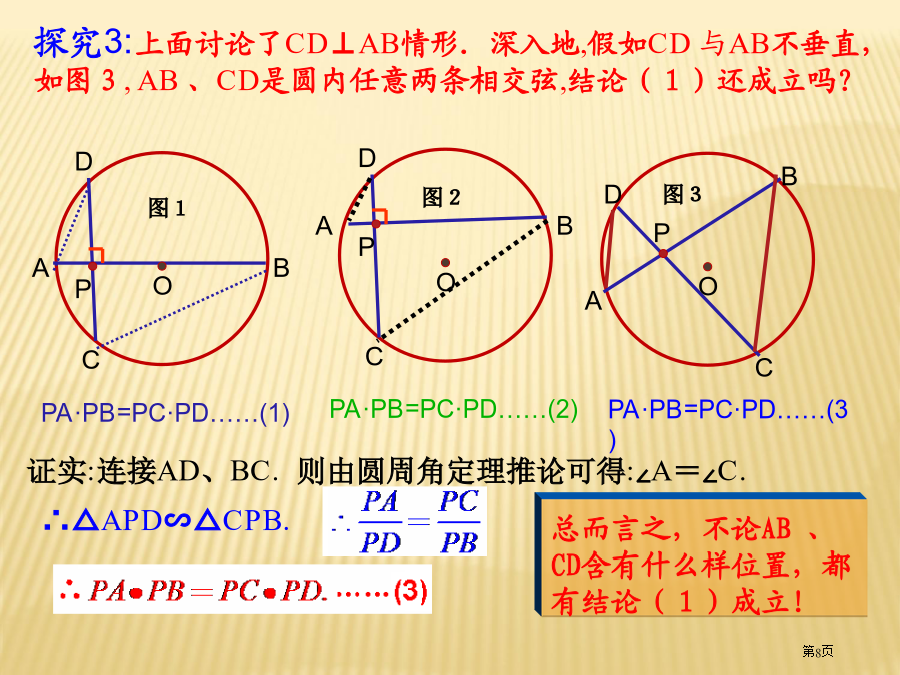
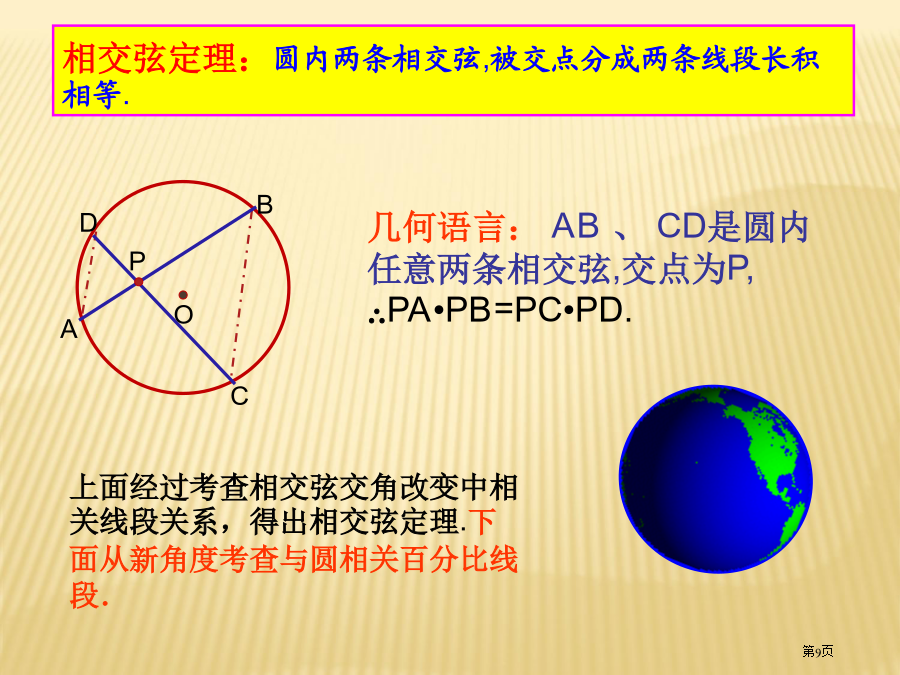
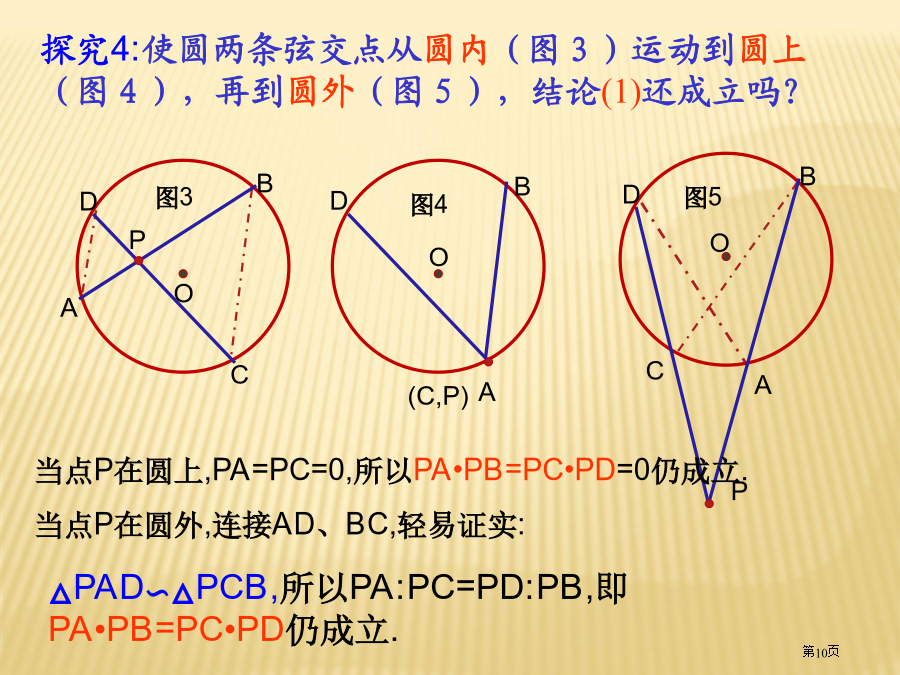
PA、PB分别切⊙O于A、B1.切线长定理从圆外一点引圆两条切线，它们切线长相等，圆心和这一点连线平分两条切线夹角，而且垂直平分切点弦。例.如图所表示PA、PB分别切圆O于A、B，并与圆O切线分别相交于C、D，已知PA=7cm，(1)求△PCD周长．(2)假如∠P=70°,求∠COD度数下面我们首先沿用从特殊到普通思绪,学习与圆相关百分比线段几个定理，希望大家做好统计.探究2:将图１中AB向上（或向下）平移,使AB不再是直径（如图２），结论（１）还成立吗？探究4:使圆两条弦交点从圆内（图３）运动到圆上（图４），再到圆外（图５），结论(1)还成立吗？如图,已知点P为⊙O外一点,割线PBA、PDC分别交⊙O于A、B和C、D.求证:PA∙PB=PC∙PD.如图,已知点P为⊙O外一点，PA切⊙O于点A，割线PCD交⊙O于C、D.求证：PA2=PC∙PD.思索：从这几个定理结论里大家能发觉什么共同点？2.联络直角三角形中射影定理，你还能想到什么？例1如图,圆内两条弦AB、CD相交于圆内一点P,已知PA=PB=4,PC=PD/4.求CD长.练习1.如图,割线PAB,PCD分别交圆于A,B和C,D.(1)已知PA=5,PB=8,PC=4,则PD=,PT=(2)已知PA=5,PB=8,PO=7,则半径R=练习2.如图,A是⊙O上一点,过A切线交直径CB延长线于点P,AD⊥BC，D为垂足.求证：PB:PD=PO:PC.课堂小结