条件概率、条件分布与条件数学期望.ppt

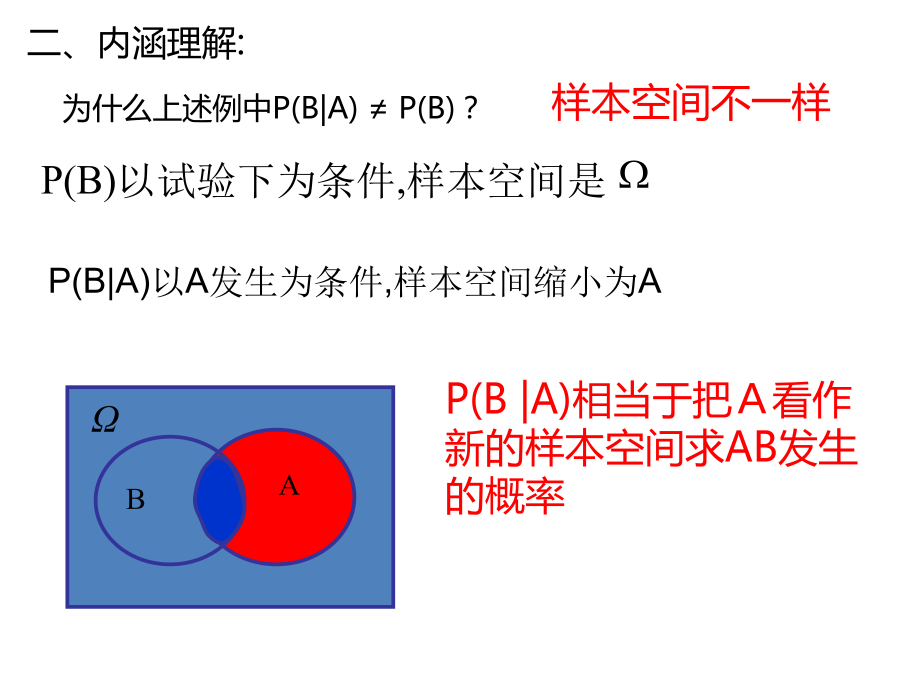
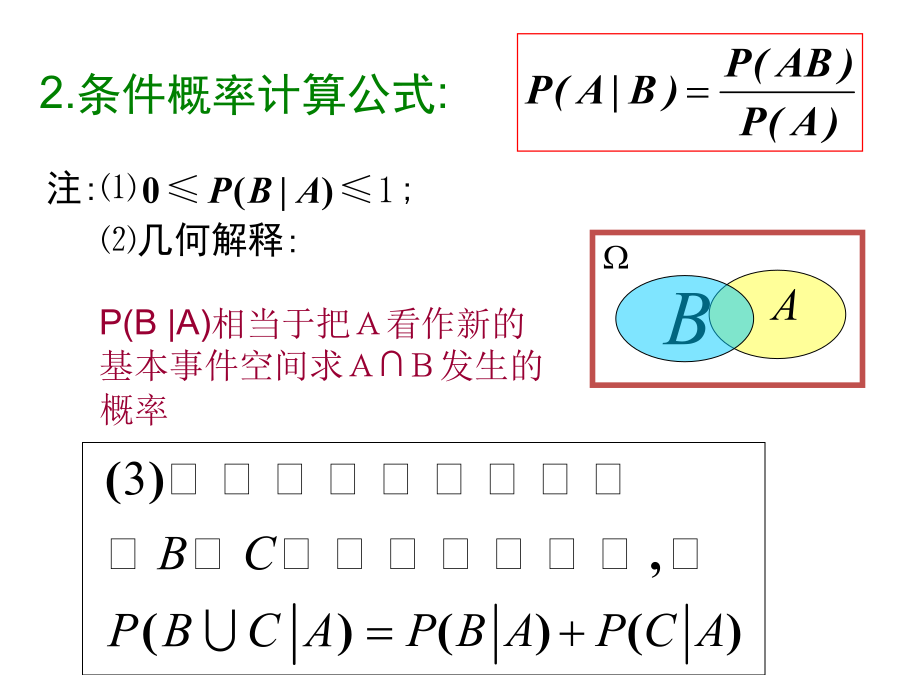
2.2.1条件概率事件概率加法公式：三张奖券中只有一张能中奖，现分别由3名同学无放回地抽取，问最后一名同学抽到中奖奖券的概率是否比前两位小？一般地，我们用W来表示所有基本事件的集合，叫做基本事件空间（或样本空间）如果已经知道第一名同学没有抽到中奖奖券，那么最后一名同学抽到中奖奖券的概率又是多少？P(B)以试验下为条件,样本空间是一般地，设A，B为两个事件，且P(A)>0，则(通常适用古典概率模型)一般地,设Ａ，Ｂ为两个事件,且Ｐ（A）＞０，称2.条件概率计算公式:反思3.概率P(B|A)与P(AB)的区别与联系例1：在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；例1、在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；例1：在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；法一：由（1）（2）可得，在第一次抽到理科题的条件下，第二次抽到理科题的概率为例2一张储蓄卡的密码共有6位数字，每位数字都可从0—9中任选一个。某人在银行自动取款机上取钱时，忘记了密码的最后一位数字，求：（1）任意按最后一位数字，不超过2次就按对的概率；（2）如果他记得密码的最后一位是偶数，不超过2次就按对的概率。练习：设100件产品中有70件一等品，25件二等品，规定一、二等品为合格品．从中任取1件，求(1)取得一等品的概率；(2)已知取得的是合格品，求它是一等品的概率．反思在某次外交谈判中，中外双方都为了自身的利益而互不相让，这时对方有个外交官提议以抛掷一颗骰子决定,若已知出现点数不超过3的条件下再出现点数为奇数则按对方的决议处理，否则按中方的决议处理，假如你在现场，你会如何抉择？例2考虑恰有两个小孩的家庭.（1）若已知（2）若已知（假定生男生女为等可能）在某次外交谈判中，中外双方都为了自身的利益而互不相让，这时对方有个外交官提议以抛掷一颗骰子决定,若已知出现点数不超过3的条件下再出现点数为奇数则按对方的决议处理，否则按中方的决议处理，假如你在现场，你会如何抉择？探究：引例:掷红、蓝两颗骰子,设事件A=“蓝色骰子的点数为3或6”事件B=“两颗骰子点数之和大于8”求(1)P(A)，P(B)，P(AB)(2)在“事件A已发生”的附加条件下事件Ｂ发生的概率？(3)比较(2)中结果与P(AB)的大小及三者概率之间关系1.条件概率对任意事件A和事件B，在已知事件A发生的条件下事件B发生的条件概率”，叫做条件概率。记作P(B|A).3.概率P(B|A)与P(AB)的区别与联系例1在5道题中有3道理科题和2道文科题，如果不放回的依次抽取2道题（1）第一次抽到理科题的概率（2）第一次与第二次都抽到理科题的概率（3）第一次抽到理科题的条件下，第二次抽到理科题的概率.例1在5道题中有3道理科题和2道文科题，如果不放回的依次抽取2道题（1）第一次抽到理科题的概率（2）第一次与第二次都抽到理科题的概率（3）第一次抽到理科题的条件下，第二次抽到理科题的概率.练习、1、5个乒乓球，其中3个新的，2个旧的，每次取一个，不放回的取两次，求：（1）第一次取到新球的概率；（2）第二次取到新球的概率；（3）在第一次取到新球的条件下第二次取到新球的概率。条件概率计算中注意的问题例2一张储蓄卡的密码共有6位数字，每位数字都可从0—9中任选一个。某人在银行自动取款机上取钱时，忘记了密码的最后一位数字，求：（1）任意按最后一位数字，不超过2次就按对的概率；（2）如果他记得密码的最后一位是偶数，不超过2次就按对的概率。例3甲、乙两地都位于长江下游，根据一百多年的气象记录，知道甲、乙两地一年中雨天占的比例分别为20%和18%，两地同时下雨的比例为12%，问：（1）乙地为雨天时，甲地为雨天的概率为多少？（2）甲地为雨天时，乙地也为雨天的概率为多少？练一练3.设100件产品中有70件一等品，25件二等品，规定一、二等品为合格品．从中任取1件，求(1)取得一等品的概率；(2)已知取得的是合格品，求它是一等品的概率．4、一批产品中有4%的次品，而合格品中一等品占45%.从这批产品中任取一件，求该产品是一等品的概率．解6、全年级100名学生中，有男生（以事件A表示）80人，女生20人；来自北京的（以事件B表示）有20人，其中男生12人，女生8人；免修英语的（以事件C表示）40人中，有32名男生，8名女生。求7、甲，乙，丙3人参加面试抽签，每人的试题通过不放回抽签的方式确定。假设被抽的10个试题签中有4个是难题签，按甲先，乙次，丙最后的次序抽