
素材-全国-2006_对称原理及应用 新课标 人教版.rar

是来****文章







在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

素材-全国-2006_对称原理及应用 新课标 人教版.rar
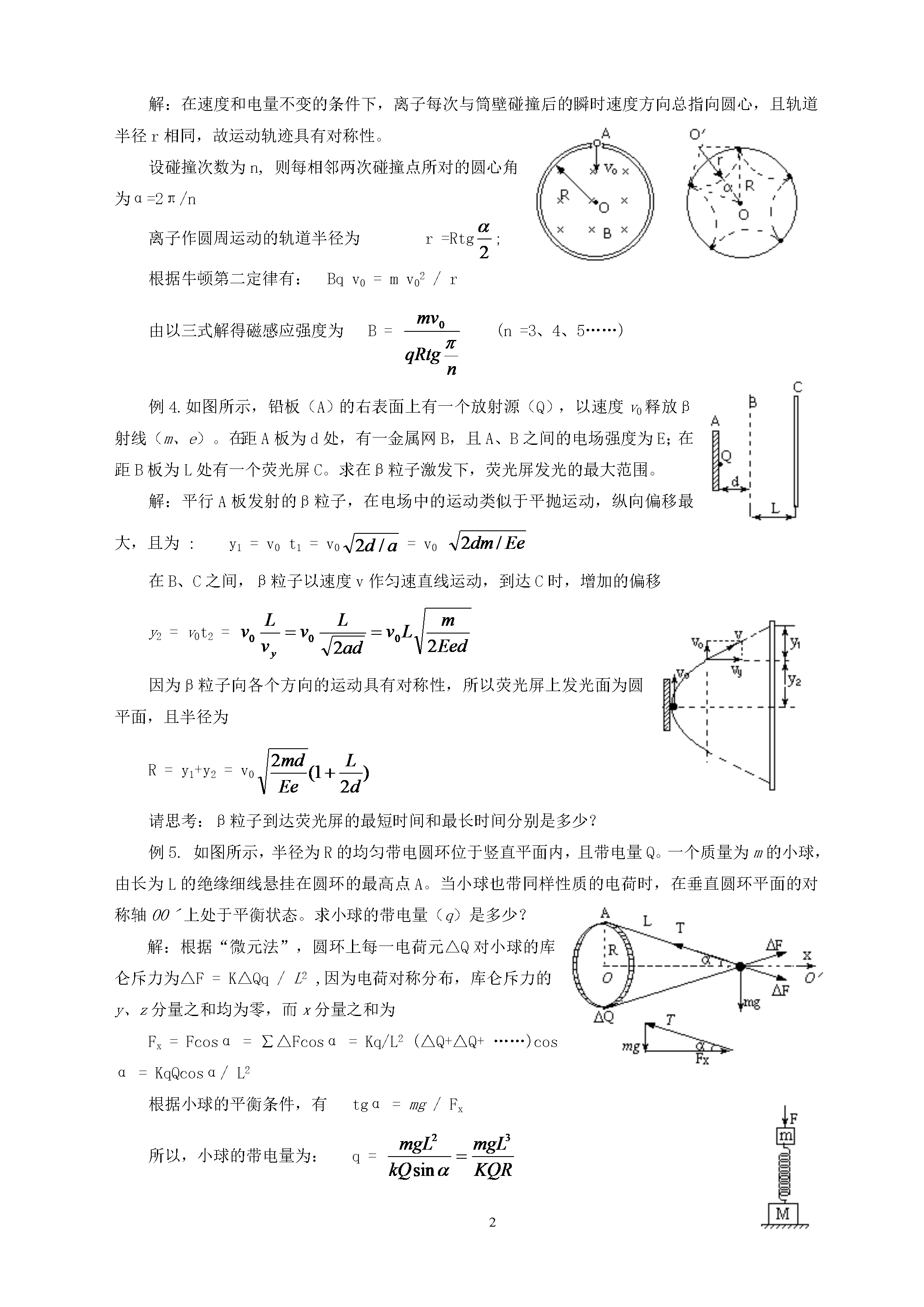
8对称原理及应用http://www.DearEDU.com重庆铝城中学牟长元所谓对称原理,就是指在对称的条件下,一定的物理规律可以等效地迁移(不论在同一问题的不同过程中,还是在两个截然不同性质的问题中),从而避免繁琐的数学推证,一下抓住问题的物理本质,迅速而简捷地解决问题。因为对称与不变具有等价性,所在在物理学中,对称具有更深的含义和广泛的应用,如物理规律的每一种对称性,都与一个守恒定律相对应;物理规律不随时间的推移或反演而变化——能量守恒定律;物理规律不随空间平移而变化——动量定恒定律;……从科学思维

素材-全国-2006_地形对气候的影响原理再现 新课标 人教版.rar
用心爱心专心118号编辑4地形对气候的影响原理再现http://www.DearEDU.com江苏省昆山市亭林中学贺志强215341地形对气候的影响是多方面的,也是错综复杂的。高大的山脉和高原的热力作用和动力作用十分巨大,能对气候发生重大的影响,与海陆分布和洋流对气候的影响作用同样重要。局部地形由于海拔高度、坡向、坡度和地形形态的差异,可在短距离内产生显著不同的局地气候。由于地形的作用,进一步破坏气候的纬度地带性,导致地面气候更加复杂多样。根据陆地的海拔高度和起伏形势,陆地地形可分为山地、高原、平原、丘陵

对称原理及应用 新课标 人教版.rar
8对称原理及应用http://www.DearEDU.com重庆铝城中学牟长元所谓对称原理,就是指在对称的条件下,一定的物理规律可以等效地迁移(不论在同一问题的不同过程中,还是在两个截然不同性质的问题中),从而避免繁琐的数学推证,一下抓住问题的物理本质,迅速而简捷地解决问题。因为对称与不变具有等价性,所在在物理学中,对称具有更深的含义和广泛的应用,如物理规律的每一种对称性,都与一个守恒定律相对应;物理规律不随时间的推移或反演而变化——能量守恒定律;物理规律不随空间平移而变化——动量定恒定律;……从科学思维

素材-全国-2006_逆温现象 新课标 人教版.rar
逆温现象逆温现象对流层大气的热量主要直接来自地面的长波辐射。一般情况下,离地面越远,气温越低,即气温随高度增加而递减,平均垂直递减离为0.6℃/100米。但在一定条件下,对流层的某一高度有时也会出现气温随高度增加而递增的现象,这种气温逆转的现象就是逆温。成因类型辐射逆温:在晴朗无风或微风的夜晚,地面辐射很快冷却,贴近地面的大气层也随之降温。由于空气愈近,降温愈多;离地面愈远,降温愈少,因而开成了自地南开始的逆温(见下图)。随着地面辐射冷却速度加快,逆温逐渐向上扩展,透明时达最强。一般日出后,太阳辐射逐渐增
素材-全国-2006_电场与磁场的对比 新课标 人教版.rar
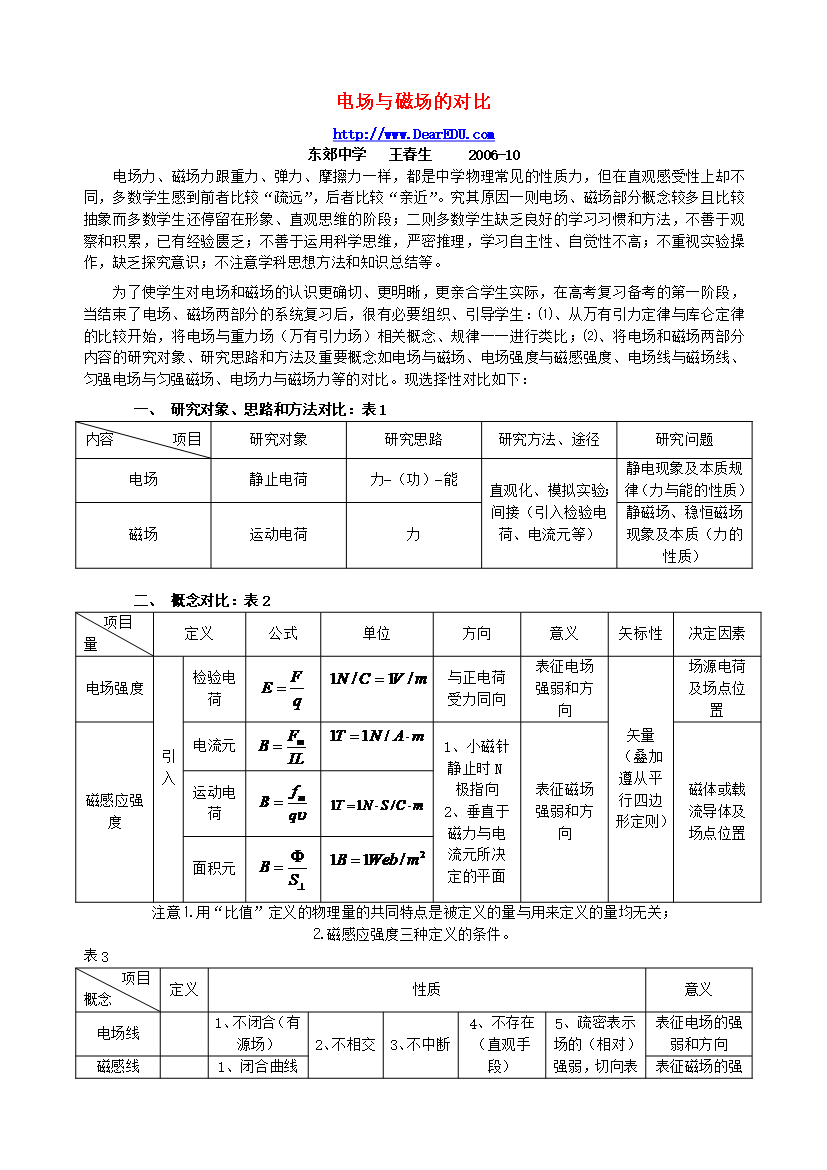
电场与磁场的对比http://www.DearEDU.com东郊中学王春生2006-10电场力、磁场力跟重力、弹力、摩擦力一样,都是中学物理常见的性质力,但在直观感受性上却不同,多数学生感到前者比较“疏远”,后者比较“亲近”。究其原因一则电场、磁场部分概念较多且比较抽象而多数学生还停留在形象、直观思维的阶段;二则多数学生缺乏良好的学习习惯和方法,不善于观察和积累,已有经验匮乏;不善于运用科学思维,严密推理,学习自主性、自觉性不高;不重视实验操作,缺乏探究意识;不注意学科思想方法和知识总结等。为了使学生对电
