
ARIMA模型预测.docx

书生****ma




亲,该文档总共13页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

ARIMA模型预测.docx
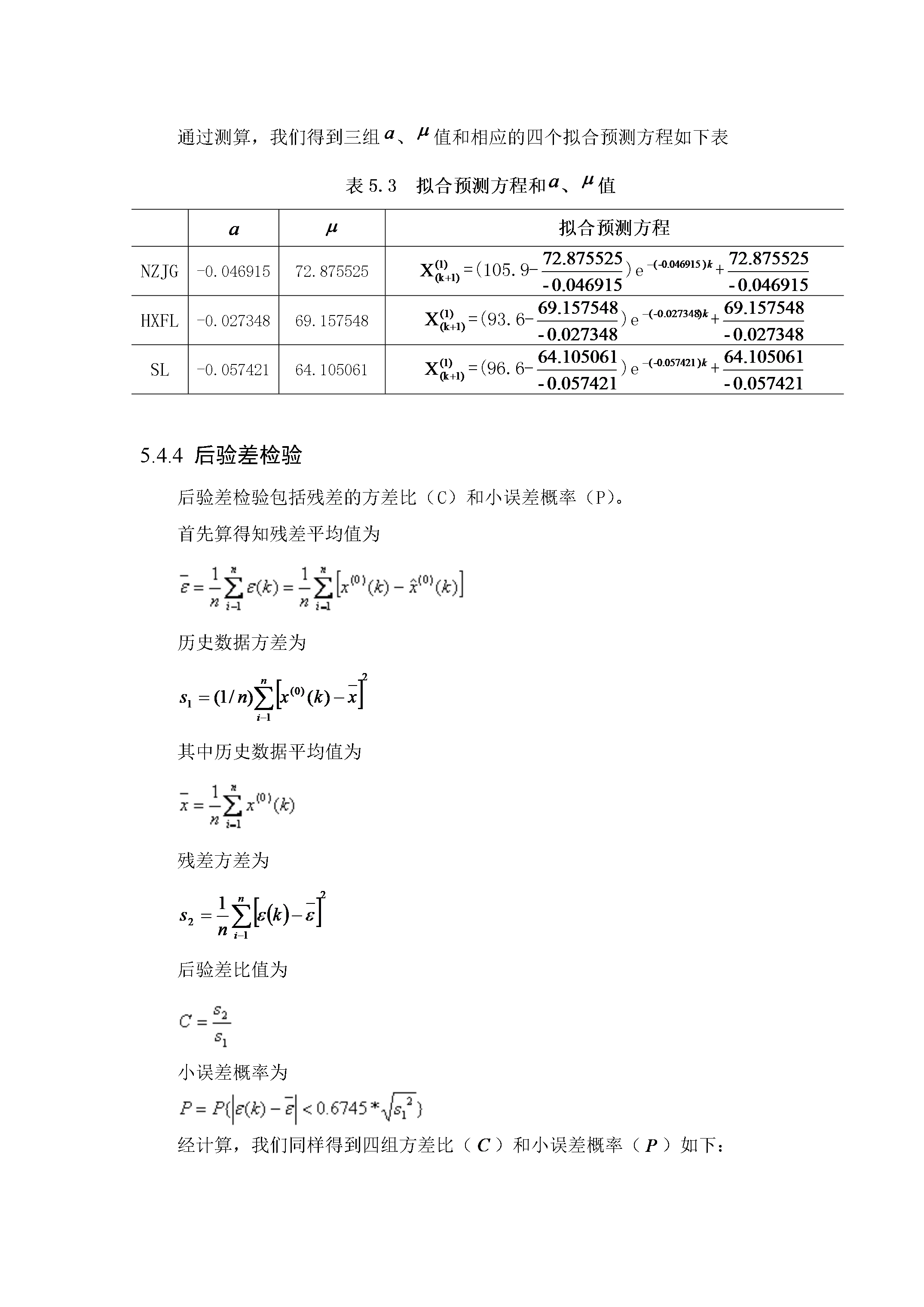
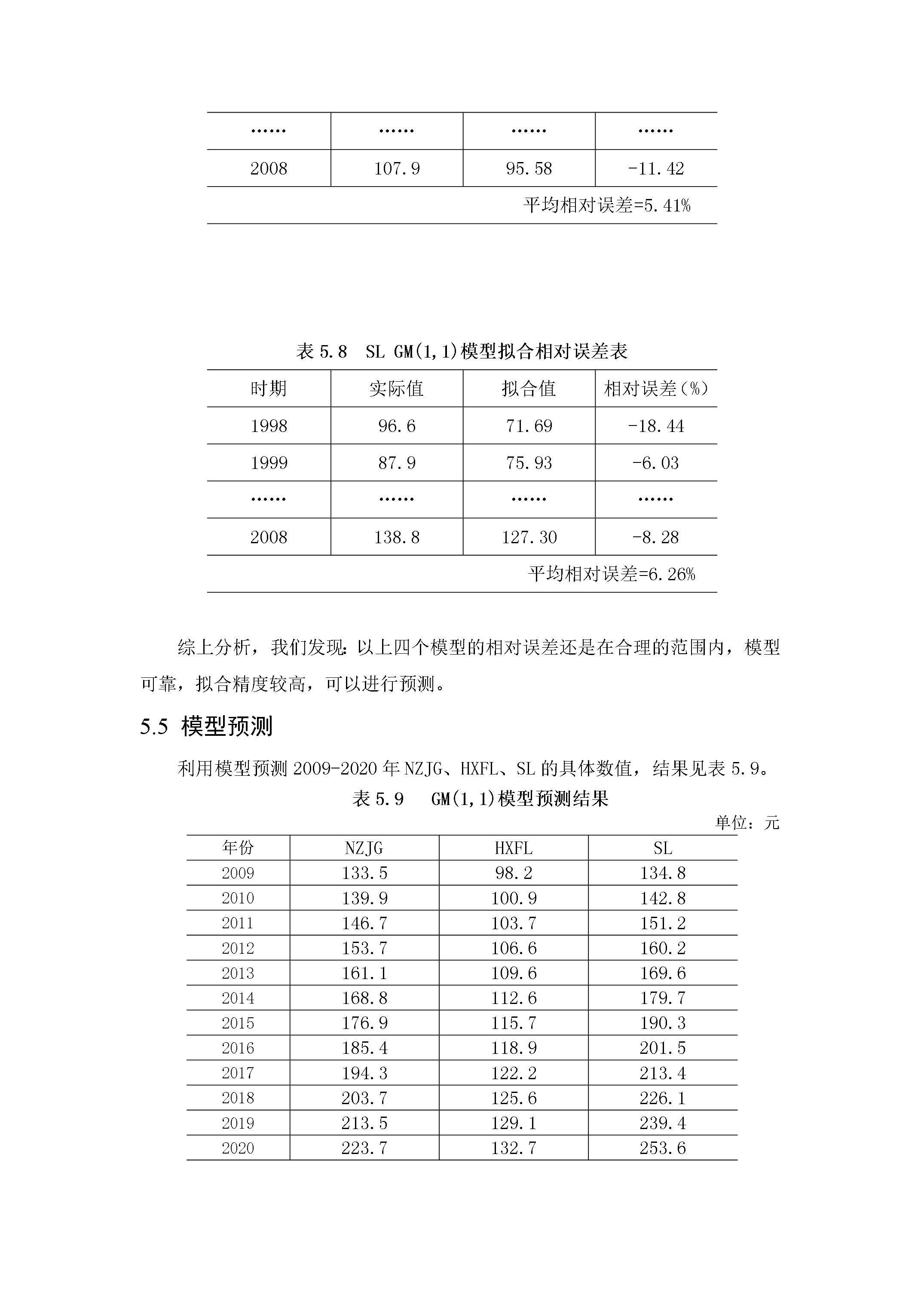
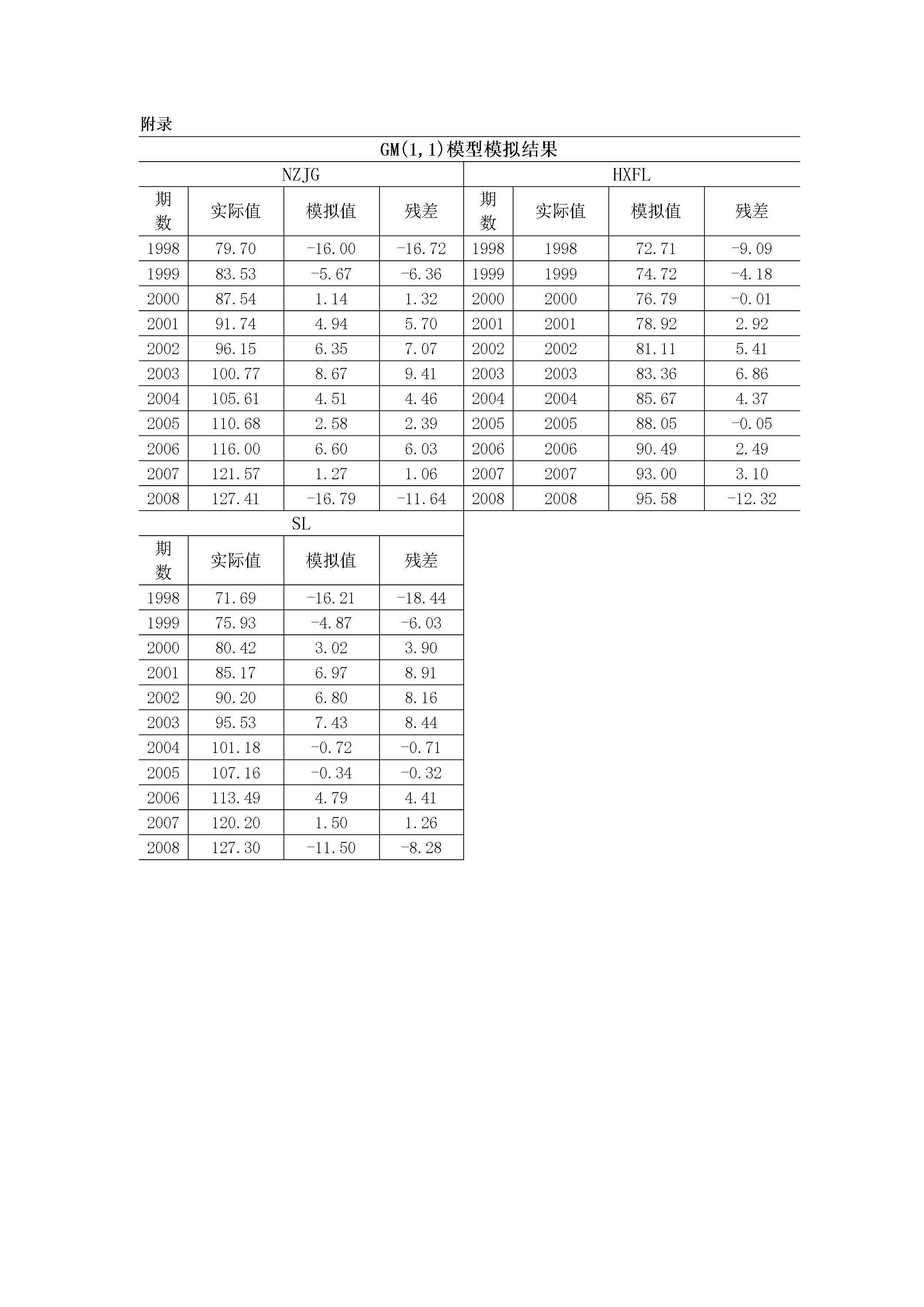
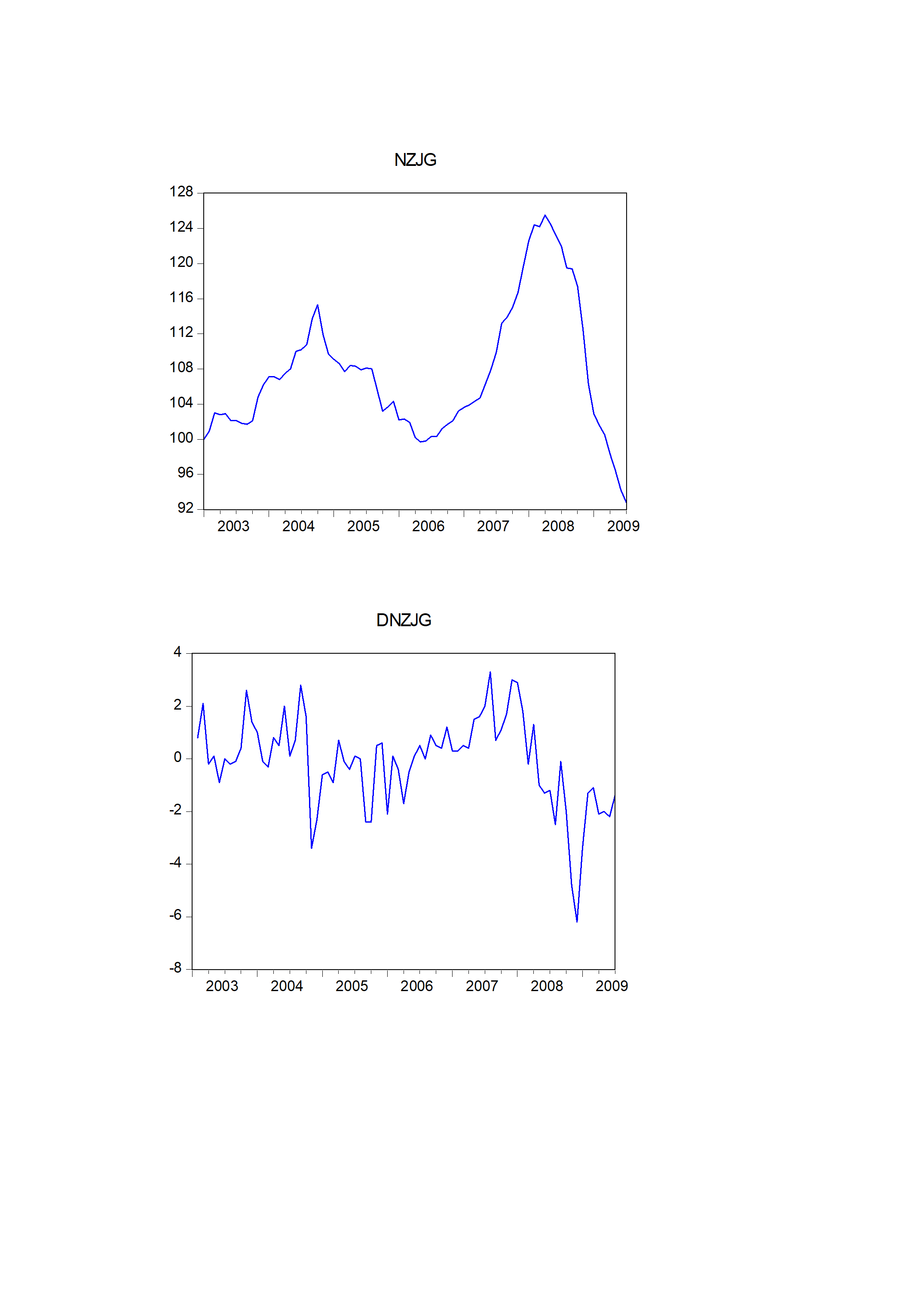
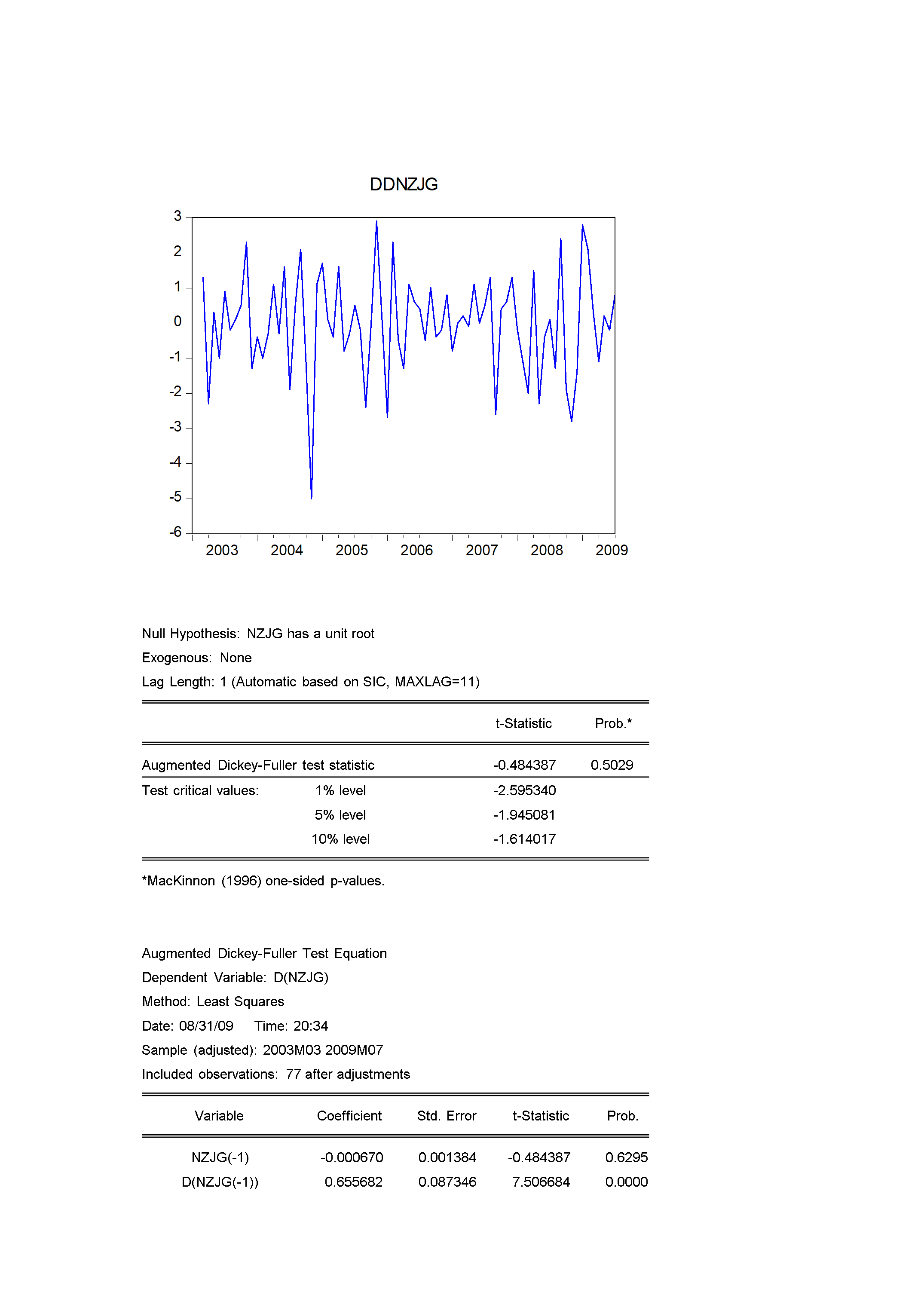
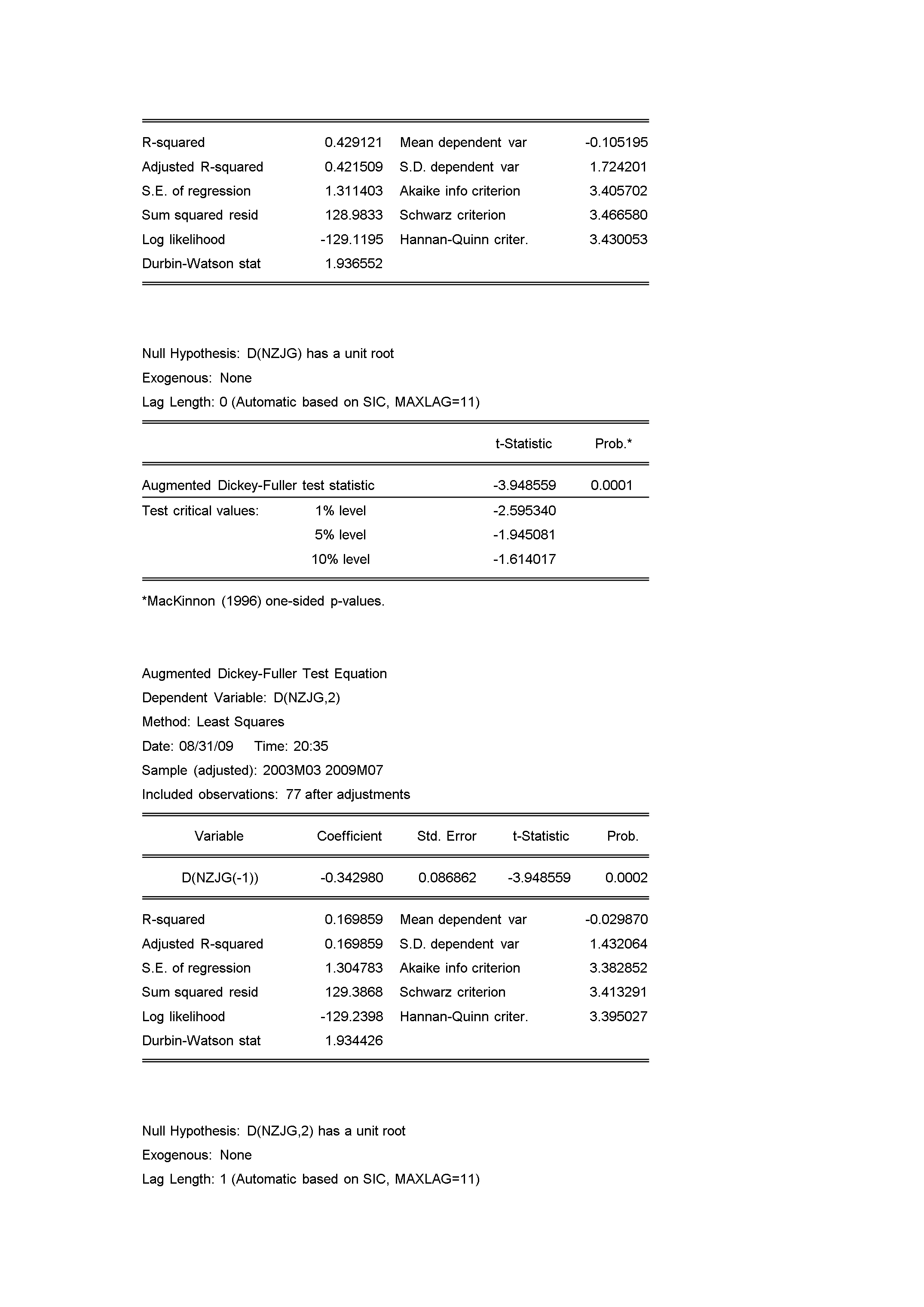
5ARIMA模型预测5.1模型选取目前,学术界较为成熟的预测方法很多,各种不同的预测方法有其所面向的特定对象,不存在一种普遍“最好”的预测方法。GM(1,1)模型预测是以灰色系统理论为基础,通过原始数据的分析处理和建立灰色模型,对系统未来状态作出科学的定量预测的一种方法。我们采用GM(1,1)模型是基于以下两方面的考虑:第一,GM(1,1)模型对数据要求较低,而其他多数预测方法以数理统计为基础,对样本量有较高要求。我们用来做预测的数据时序只有14年,预测使用GM(1,1)模型较好;第二,GM(1,1)模型

ARIMA模型预测.docx
5ARIMA模型预测5.1模型选取目前,学术界较为成熟的预测方法很多,各种不同的预测方法有其所面向的特定对象,不存在一种普遍“最好”的预测方法。GM(1,1)模型预测是以灰色系统理论为基础,通过原始数据的分析处理和建立灰色模型,对系统未来状态作出科学的定量预测的一种方法。我们采用GM(1,1)模型是基于以下两方面的考虑:第一,GM(1,1)模型对数据要求较低,而其他多数预测方法以数理统计为基础,对样本量有较高要求。我们用来做预测的数据时序只有14年,预测使用GM(1,1)模型较好;第二,GM(1,1)模型

ARIMA模型预测.docx
5ARIMA模型预测5.1模型选取目前,学术界较为成熟的预测方法很多,各种不同的预测方法有其所面向的特定对象,不存在一种普遍“最好”的预测方法。GM(1,1)模型预测是以灰色系统理论为基础,通过原始数据的分析处理和建立灰色模型,对系统未来状态作出科学的定量预测的一种方法。我们采用GM(1,1)模型是基于以下两方面的考虑:第一,GM(1,1)模型对数据要求较低,而其他多数预测方法以数理统计为基础,对样本量有较高要求。我们用来做预测的数据时序只有14年,预测使用GM(1,1)模型较好;第二,GM(1,1)模型

ARIMA模型预测.docx
5ARIMA模型预测5.1模型选取目前学术界较为成熟的预测方法很多各种不同的预测方法有其所面向的特定对象不存在一种普遍“最好”的预测方法。GM(11)模型预测是以灰色系统理论为基础通过原始数据的分析处理和建立灰色模型对系统未来状态作出科学的定量预测的一种方法。我们采用GM(11)模型是基于以下两方面的考虑:第一GM(11)模型对数据要求较低而其他多数预测方法以数理统计为基础对样本量有较高要求。我们用来做预测的数据时序只有14年预测使用GM(11)模型较好;第二GM(11)模型的计算量相对较小计算方法

ARIMA模型预测.docx
5ARIMA模型预测5.1模型选取目前学术界较为成熟的预测方法很多各种不同的预测方法有其所面向的特定对象不存在一种普遍“最好”的预测方法。GM(11)模型预测是以灰色系统理论为基础通过原始数据的分析处理和建立灰色模型对系统未来状态作出科学的定量预测的一种方法。我们采用GM(11)模型是基于以下两方面的考虑:第一GM(11)模型对数据要求较低而其他多数预测方法以数理统计为基础对样本量有较高要求。我们用来做预测的数据时序只有14年预测使用GM(11)模型较好;第二GM(11)模型的计算量相对较小计算方法
