
流体力学课件6气体射流.ppt

和蔼****娘子








亲,该文档总共29页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

流体力学课件6气体射流.ppt
流体力学课件6气体射流按照喷口形状,又可分为圆射流、矩形射流和条缝射流。圆形射流是轴对称射流。如矩形喷口的长短边之比(a:b)不超过3:1时,矩形射流能够迅速发展为圆形射流,只需要根据当量直径,就可采用圆形射流公式进行计算。当矩形喷口长短边之比超过10:1时,就属于条缝射流,条缝射流又称为平面射流。按照射流的流态,有层流射流和紊流射流。气体淹没射流的流态一般都是紊流,层流射流几乎是不存在的。本节讨论无限空间气体紊流淹没射流,简称气体紊流射流。这里需要指出的是,射流与周围气体温度相同。本节主要研究气体紊流射

流体力学气体射流ppt课件.ppt
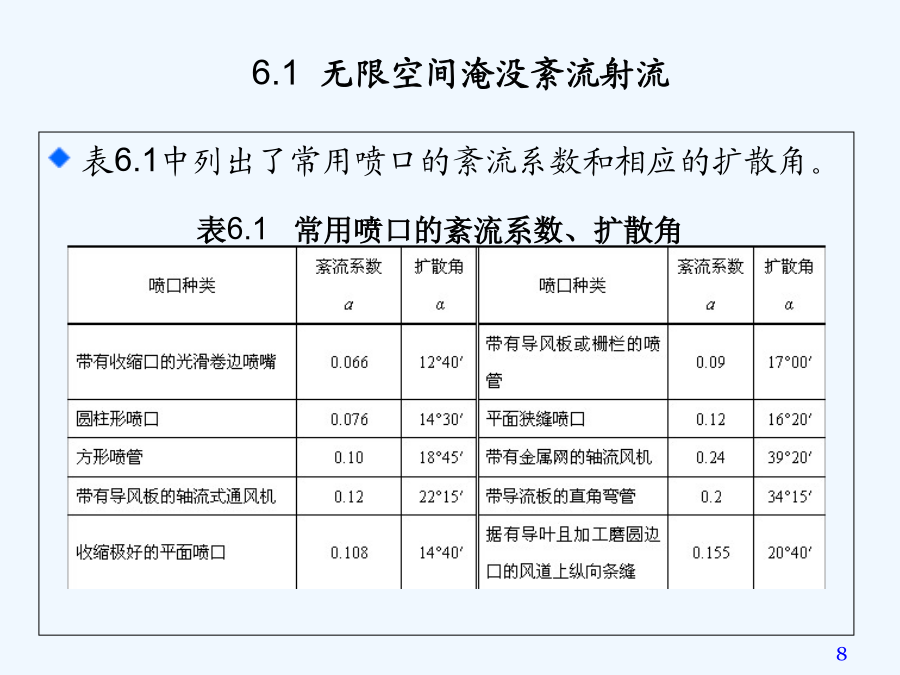
6.1无限空间淹没紊流射流流体经孔口或管嘴流出,流入另一部分流体介质中的流动现象,称为射流。在供热通风与空调工程中,对所遇射流可进行如下简单分类。依照射流的流体种类,有气体射流和液体射流。按射流与射流流入空间的流体是否同相,有淹没射流和自由射流。按照出流空间大小、对射流的流动是否有影响,有无限空间射流和有限空间射流。当流动空间很大,射流基本不受周围固体边壁的影响,称为无限空间射流。按照喷口形状,又可分为圆射流、矩形射流和条缝射流。圆形射流是轴对称射流。如矩形喷口的长短边之比(a:b)不超过3:1时,矩形射

《流体力学》第六章气体射流ppt课件.ppt
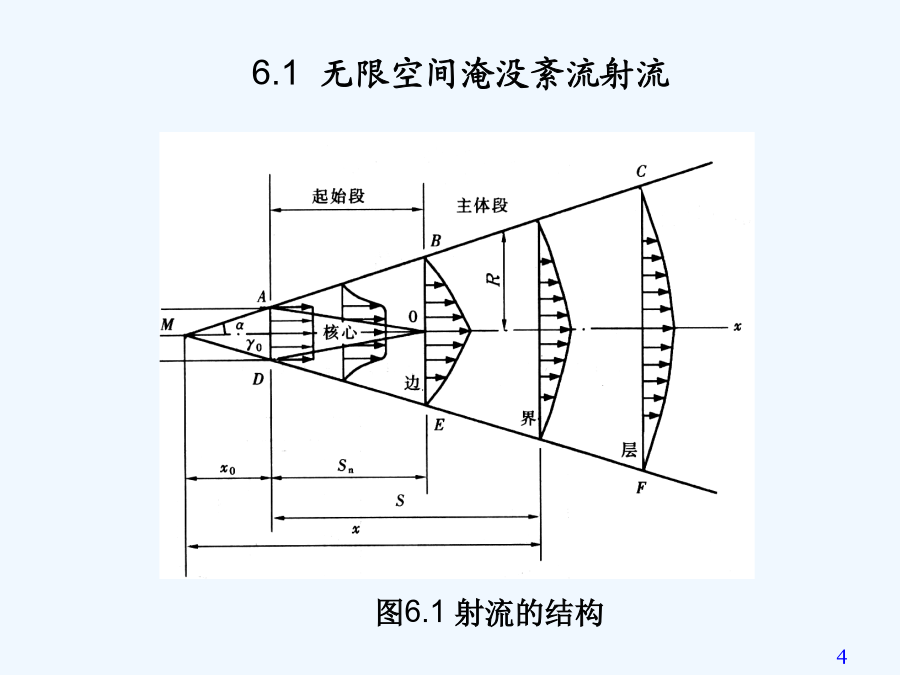
第六章气体射流第一节无限空间淹没紊流射流的特征射流核心边界层过渡断面(转折断面)起始段及主体段扩散角(极角)喷嘴种类平面壁上锐缘狭缝由可得:由两图中可见:无论主体段或起始段内,轴心速度最大,从轴心向边界层边缘,速度逐渐减小至零。距喷嘴距离越远,即x值增大,边界层厚度越大,而轴心速度则越小,也就是说,随着x的增大,速度分布曲线不断地扁平化了。注意几个符号的含义:用半经验公式表示射流各横截面上的无因次速度分布为:动力特征:圆断面射流为例应用动量守恒原理截面上动量流量为任意横截面上的动量流量则需积分第二节圆断面

《流体力学》第六章气体射流.ppt
第六章气体射流第一节无限空间淹没紊流射流的特征射流核心边界层过渡断面(转折断面)起始段及主体段扩散角(极角)喷嘴种类平面壁上锐缘狭缝由可得:由两图中可见:无论主体段或起始段内,轴心速度最大,从轴心向边界层边缘,速度逐渐减小至零。距喷嘴距离越远,即x值增大,边界层厚度越大,而轴心速度则越小,也就是说,随着x的增大,速度分布曲线不断地扁平化了。注意几个符号的含义:用半经验公式表示射流各横截面上的无因次速度分布为:动力特征:圆断面射流为例应用动量守恒原理截面上动量流量为任意横截面上的动量流量则需积分第二节圆断面

气体射流_.doc
气体射流1.圆射流以Q0=0.55m³/s,从d0=0.3m管嘴流出。试求2.1m处射流半宽度R,轴心速度,断面平均流速,质量平均,并进行比较。解:查表知:a=0.08由在主体段=3.4∴R=3.4×0.15=0.72m===7.78m/s解得:解得:解得:2.某体育馆的圆柱形送风口,d0=0.6m,风口至比赛区为60m,要求比赛区风速(质量平均风速)不得超过0.3m/s,求送风口送风量应不超过多少m³/s?解:查表知:a=0.08由在主体段(其中)解得:3.岗位送风所设风口向下,距地面4m。要求在工作区
