
第五章地下水向边界附近井的运动.ppt

和蔼****娘子









亲,该文档总共28页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第五章地下水向边界附近井的运动.ppt
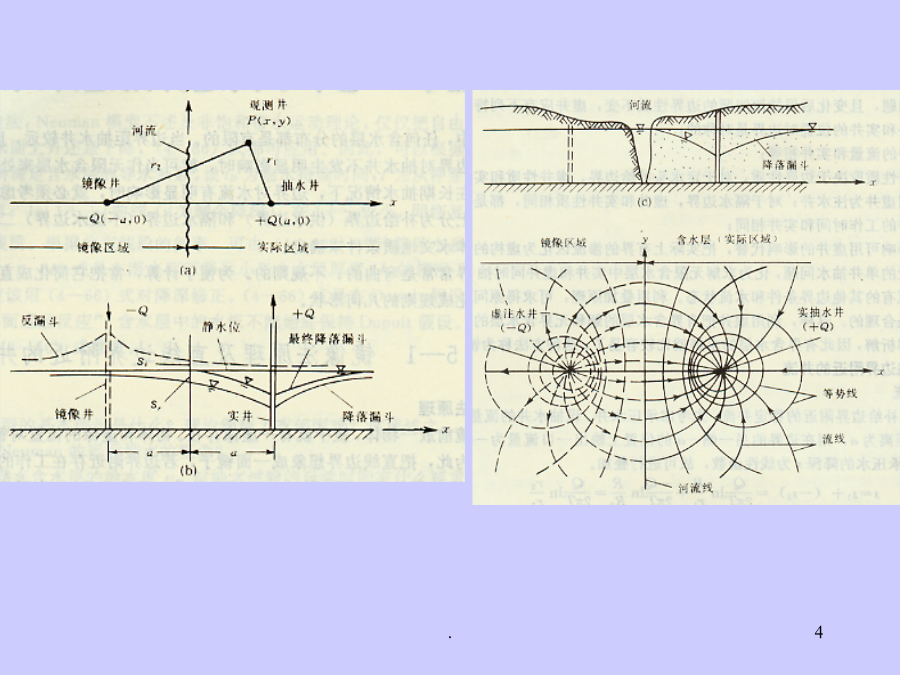
第五章地下水向边界附近井的运动前面讨论的是地下水向井的运动,都是在无限含水层中,这一章讨论边界附近井的地下水运动。在解析解中,我们只能将边界概化为;补给边界(供水边界)和隔水边界(不透水边界)。§1镜象法原理及直线边界附近的井流一、镜象法原理没有边界时,抽水井的水位线为最下边的漏斗线;有补给边界附近时,水头线为中间的线,相当于在补给边界的另一侧有一注水井,然后进行叠加的结果。因此,边界的影响可用虚井的影响代替,把实际上有界的渗流区化为虚构的无限渗流区,把求解边界附近的单井抽水问题,化为求解无限含水层中实井

第五章-地下水向边界附近井的运动PPT课件.ppt
第五章地下水向边界附近井的运动前面讨论的是地下水向井的运动,都是在无限含水层中,这一章讨论边界附近井的地下水运动。在解析解中,我们只能将边界概化为;补给边界(供水边界)和隔水边界(不透水边界)。§1镜象法原理及直线边界附近的井流一、镜象法原理没有边界时,抽水井的水位线为最下边的漏斗线;有补给边界附近时,水头线为中间的线,相当于在补给边界的另一侧有一注水井,然后进行叠加的结果。因此,边界的影响可用虚井的影响代替,把实际上有界的渗流区化为虚构的无限渗流区,把求解边界附近的单井抽水问题,化为求解无限含水层中实井

地下水向边界附近井的运动一填空题1.docx
第五章地下水向边界附近井的运动一、填空题1.应用映射法时,若实井为抽水井,那么对于定水头补给边界进行映射时,虚井为_____;如果对于隔水边界进行映射,虚井为_____。2.对于有界含水层的求解,一般把边界的影响用_____的影响来代替。3.直线补给边界附近的抽水井,当抽水降落漏斗还没有扩展到边界时,水流为_____流;当降落漏斗扩展到了边界时,水流趋于_____流。4.当直线边界的方位未知时,则至少需要_____个观测孔的资料才能确定边界的方位。5.对直线补给边界附近的抽水井来说,井流量中的补给量占井流

地下水向完整井的稳定运动.docx
地下水动力学习题主讲:肖长来教授卞建民博士3地下水向完整井的稳定运动要点:本章是全书的重点之一,主要介绍地下水向完整井的稳定运动理论及相应计算公式,包括裘布依(Dupuit)公式、蒂姆(Thiem)公式、非线性层流井流公式、井流量与降深间的随机关系式以及均匀流中的井流公式。通过本章习题的练习,要求学生在掌握稳定井流理论的基础上,能熟练利用计算公式确定相应条件下的水井涌水量(或水头)和含水层的渗透系数(或导水系数),提高分析和解决实际问题的能力。表3—1给出了用稳定流抽水试验资料求渗透系数的公式。3.1井流

地下水向完整井的稳定运动PPT.ppt
第三章地下水向完整井的稳定运动§3.1水井的分类及井流特征3.1.1水井分类水井(waterwell)是常用的集水建筑物,用以开采、排泄地下水。可分为水平集水建筑物(排水沟、集水管、集水廊道等)和垂直集水建筑物(钻孔、水井、竖井等)。(1)按井径大小和成井方法:管井、筒井。管井(pipewell)是直径通常小于0.5m、深度比较大、采用钻机开凿的水井。筒井是直径通常大于0.5m甚至数米、深度比较浅、通常用人工开挖的水井。(2)按揭穿含水层的程度及进水条件:完整井、非完整井完整井(fullypenetrat
