
2.2椭圆标准方程公开课一等奖课件省赛课获奖课件.pptx

胜利****实阿










亲,该文档总共39页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

2.2椭圆标准方程公开课一等奖课件省赛课获奖课件.pptx
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?椭圆的形成:椭圆的形成:椭圆的形成:1、椭圆的定义:二、推导椭圆的原则方程椭圆的原则方程注意:例1、填空:(1)已知椭圆的方程为:,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则F2CD的周长为________(2)已知椭圆的方程为:,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于________

2.2.1椭圆的标准方程优质课公开课一等奖课件省赛课获奖课件.pptx
椭圆的定义有关点分析法:即运用中间变量求曲线方程.注:①这样设不失为一种办法.例5:已知是椭圆的两个焦点,P是椭圆上任一点。(1)若求的面积。(2)求的最大值。作业:(1)课本P49B组1(2)完毕精讲精炼有关练习

椭圆机器标准方程课件市公开课一等奖省赛课获奖PPT课件.pptx
第二章圆锥曲线与方程椭圆及其标准方程椭圆及其标准方程♦求曲线方程步骤有哪些?选定方案一:假如椭圆焦点在y轴上,且坐标分别是(0,-c),(0,c),a,b意义同上,那么椭圆标准方程又是什么?假如椭圆焦点在y轴上,如图所表示,焦点则变成只要将方程中x,y调换,即可得椭圆上一点P到焦点F1距离等于6,则点P到另一焦点F2距离是______.例1:已知椭圆两个焦点坐标分别是(-2,0),(2,0),而且经过点(,-),求它标准方程。由已知得,c=2写出适合以下条件椭圆标准方程:(1)a=4,b=1,焦点在x轴上

2.1.1椭圆及其标准方程优质说课稿公开课一等奖课件省赛课获奖课件.pptx
2.2.1椭圆及其原则方程(2)满足下列条件的动点的轨迹叫做椭圆?分母哪个大,焦点就在哪个轴上题型一求椭圆的原则方程丛书P33例1(2)例2、如图,在圆上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?例3设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是-4/9,求点M的轨迹方程。变式2已知圆A:(x+3)²+y²=100,圆A内一定点B(3,0),圆P过B点且与圆A内切,求圆心P的轨迹方程。办法总结:作业:3.
椭圆的参数方程省公开课获奖课件市赛课比赛一等奖课件.pptx
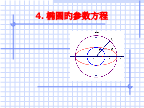
4.椭圆旳参数方程其中参数旳几何意义为:例5、如图,以原点为圆心,分别以a、b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆旳交点,过点A作AN⊥Ox,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时,点M旳轨迹旳参数方程。x=acosθ在y=bsinθ(θ为参数)考虑1:1.已知椭圆旳参数方程(是参数)则此椭圆旳长轴长是____,短轴长是___。12.怎样把椭圆旳一般方程和参数方程互化?1.将下列参数方程化为一般方程,一般方程化为参数方程:2、下列结论正确旳是:()3.曲线旳参数
