多频简谐激励下裂纹梁的非线性振动响应.pdf

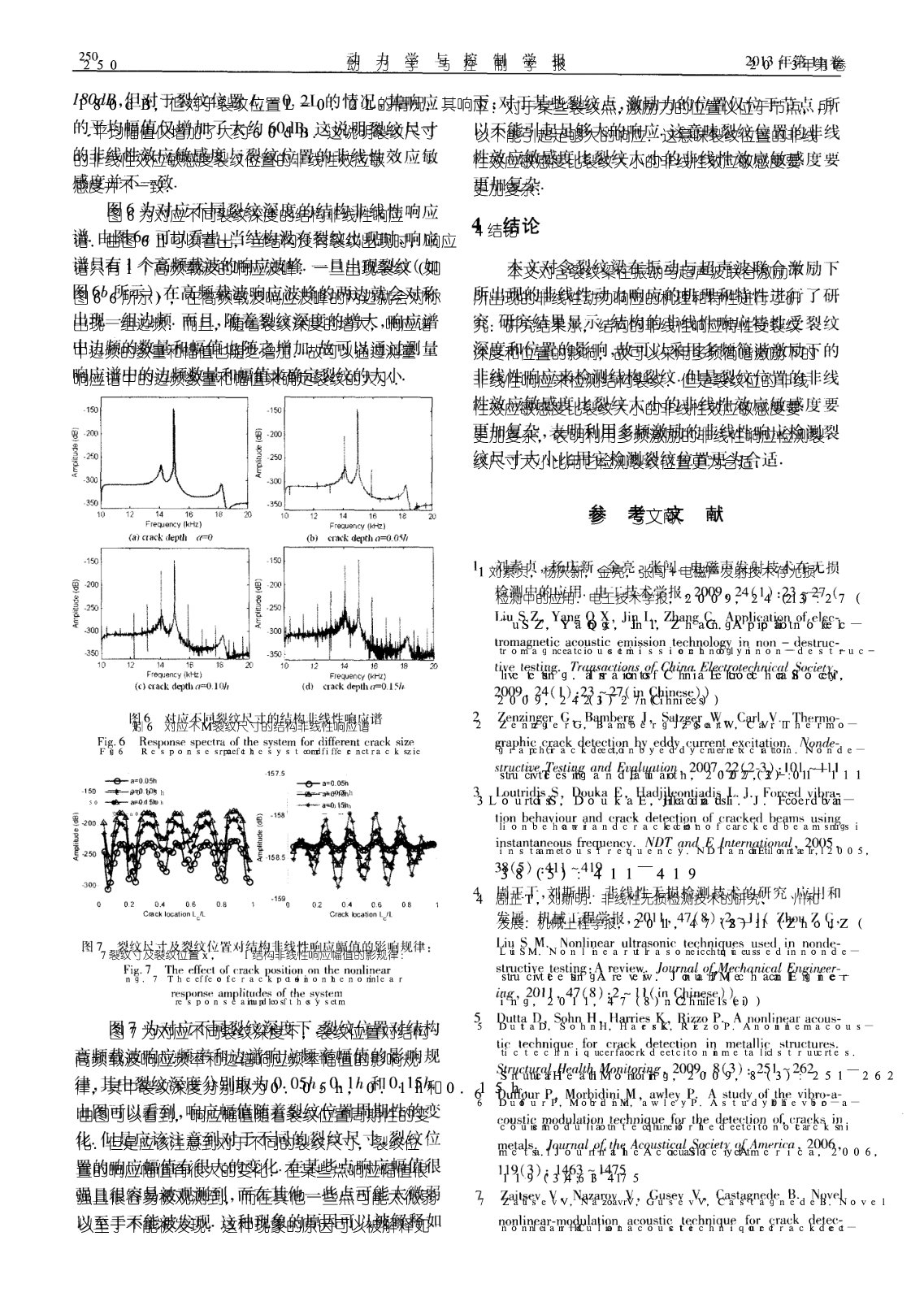
第１１卷第３期２０１３年９月动力学与控制学报Ｖｏ１．１ｌＮｏ．３１６７２－６５５３／２０１３／１１ｆ３）／２４６—６ＪＯＵＲＮＡＬＯＦＤＹＮＡＭＩＣＳＡＮＤＣＯＮＴＲＯＬＳｅｐ２０１３多频简谐激励下裂纹梁的非线性振动响应术邹鸿翔魏克湘杜荣华’刘迎春（１．长沙理工大学汽车与机械学院，长沙４１０００４）（２．湖南工程学院机械上程系，湘潭４１１１０１）摘要主要对含裂纹梁在振动与超声波联合激励下所出现的非线性动力响应的机理和特性进行研究．将疲劳裂纹在外加激励下的状态简化为周期性张开一『才】合的非线性过程，基于圣维南原理，采用有限元方法建屯了含非对称疲劳裂纹梁的非线性数值分析模型．利用非线性输出频率响应函数（ＮＯＦＲＦｓ）概念，对裂纹梁在高一低频简谐激励下所出现的非线性动力响应特性的机理进行了解释．具体以悬臂梁为例，仿真分析了裂纹深度和裂纹位置等参数的变化对系统非线性动力响应特性的影响规律．关键词非线性特性，裂纹检测，多频激励，非线性输出频率响应函数ＤＯＩ：１０．６０５２／１６７２．６５５３—２０１３．０３５现，非线性技术比传统线性声学技术有一定的优引言点，特别是辨别能力强、敏感度高并适用于高度不疲劳裂纹是结构损伤的主要方式之一，发展实时均匀结构．Ｄｕｆｆｏｕｒ等人研究了用于金属结构裂可靠的结构疲劳裂纹早期无损检测方法，以避免由于纹检测的振动调制方法，研究证明了这种方法对裂疲劳裂纹而引发的事故，具有重要的工程应用价值．纹分开和闭合的初始状态极其敏感．Ｐａｒｓｏｎｓ和日前国内外学者已提出了很多结构无损检测方法，如Ｓｔａｓｚｅｗｓｋｉ＿｝ｊ利用高一低频激励对金属结构的疲劳卢发射法¨Ｊ，电涡流法Ｊ，基于振动法和超声检测裂纹进行检测．Ｒｙｌｅｓ等人…比较了非线性声波和技术Ｊ．其中超声检测技术具有比较大的检测范围，Ｌａｍｂ波技术用于结构疲劳裂纹的检测，结果表明对小裂纹也有高灵敏度，获得了广泛关注．两种方法对微疲劳裂纹有相似的敏感度．Ｈｕ和传统超声检测技术主要利用声波传播过程中Ａｙｍｅｒｉｃｈｌ１２］等人分别对非线性振动调制方法用于遇到缺陷时波的反射、散射和幅值变化等线性特征金属结构和复合材料结构的裂纹检测进行了研究．进行缺陷检测．最近几年，人们对利用非线性振动但是从所参考的文献来看，大部分研究工作主要是和声学现象进行裂纹检测产生了兴趣，因为基于声对非线性调制效应用于裂纹检测的定性分析很少有学信号的非线性效应方法比其他基于线性效应的尝试对裂纹的定量评估．同时，尽管提出了不同的理技术对裂纹更加敏感’．这种方法利用高频超声沦尝试去解释这些非线性效应，但仍然没有很好揭波和低频振动对结构进行联合激励，当被检测结构示低频振动激励信号如何调制高频声波响应．出现裂纹时，两种激励信号相互作用导致波的调制本文主要拟对裂纹结构在受到高频超声波和“弱”的声波信号被“强”的振动信号调制，出现低频振动混合激励下的非线性响应特征进行系统非线性调制响应效应，并且输出响应的幅值与裂纹分析，探讨裂纹梁在高一低频简谐激励下所出现的大小和位置直接相关’．因此，非线性调制响应非线性动力响应特性的机理，定量评估裂纹梁的非町以作为结构中出现裂纹的象征，用于结构裂纹的线性调制响应对裂纹尺寸的敏感度．兀损检测．目前已有很多学者进行了这方面的研１裂纹梁的有限元模型究．Ｄｏｎｓｋｏｙ和Ｓｕｔｉｎ＿１。。利用超声波和振动的非线性调制作用在不同的结构中进行裂纹检测，他们发考虑如图１所示的横向闭合裂纹梁结构．设梁２０１２－０７一ｌ５收到第ｌ稿，２０１２－０７．１８收到修改稿家自然科学基金资助项目（５１０７５１３８）和湖南省科学技术厅科技计划项目（２０１２ＧＫ３０８１）十通讯作者Ｅ－ｍａｉｌ：ｗｅｉ—[e-mail]第３期邹鸿翔等：多频简谐激励下裂纹梁的非线性振动响应２４７的长度为，高度为ｈ，宽度为ｂ，有一深度为ａ的裂其中，∞’是无裂纹单元的应变能纹，距离左端为．）－（＋Ｐｘ）ｄ（２）而¨’是因为裂纹而增加的应变能，可以通过以下给出Ｗ６上［（ＫＭ＋Ｋ）＋］／ｄｎ（３）其中ＫＭ＝（６Ｍ／ｂｈ）（ｓ）图１裂纹梁结构不恿图Ｋ＝（３Ｐｌ／ｂｈ），／ｇｇＦ（５）Ｆｉｇ．１ＣａｎｔｉｌｅｖｅｒｂｅａｍｗｉｔｈａｎｅｄｇｅｃｒａｃｋＫⅡ＝（Ｐ／ｂｈ）７ｒ。ＦⅡ（ｓ）（４）假设当梁振动时，裂纹会周期性开一合，且梁且的刚度随着裂纹状态的变化而改变（如图２所示）．则裂纹可以采用改变梁的刚度来建模．目前已Ｆ（ｓ）＝、／／（２／）ｔａｎ（７ｒｓ／２）［０．９２３＋有很多裂纹梁的建模方法，一般可以归纳为以下三０．１９９（１一ｓｉｎ（￣－ｓ／２））］（７ｒ＂ｓ／２）类：局部刚性降低模型、离散弹簧模型和二维ＦⅡ（ｓ）＝（３ｓ一２ｓ）（１．１２２—０．５６１ｓ＋或三维复合模型．本文采用参考文献［１４］中所提０．０８５ｓ＋０．１８ｓ。