
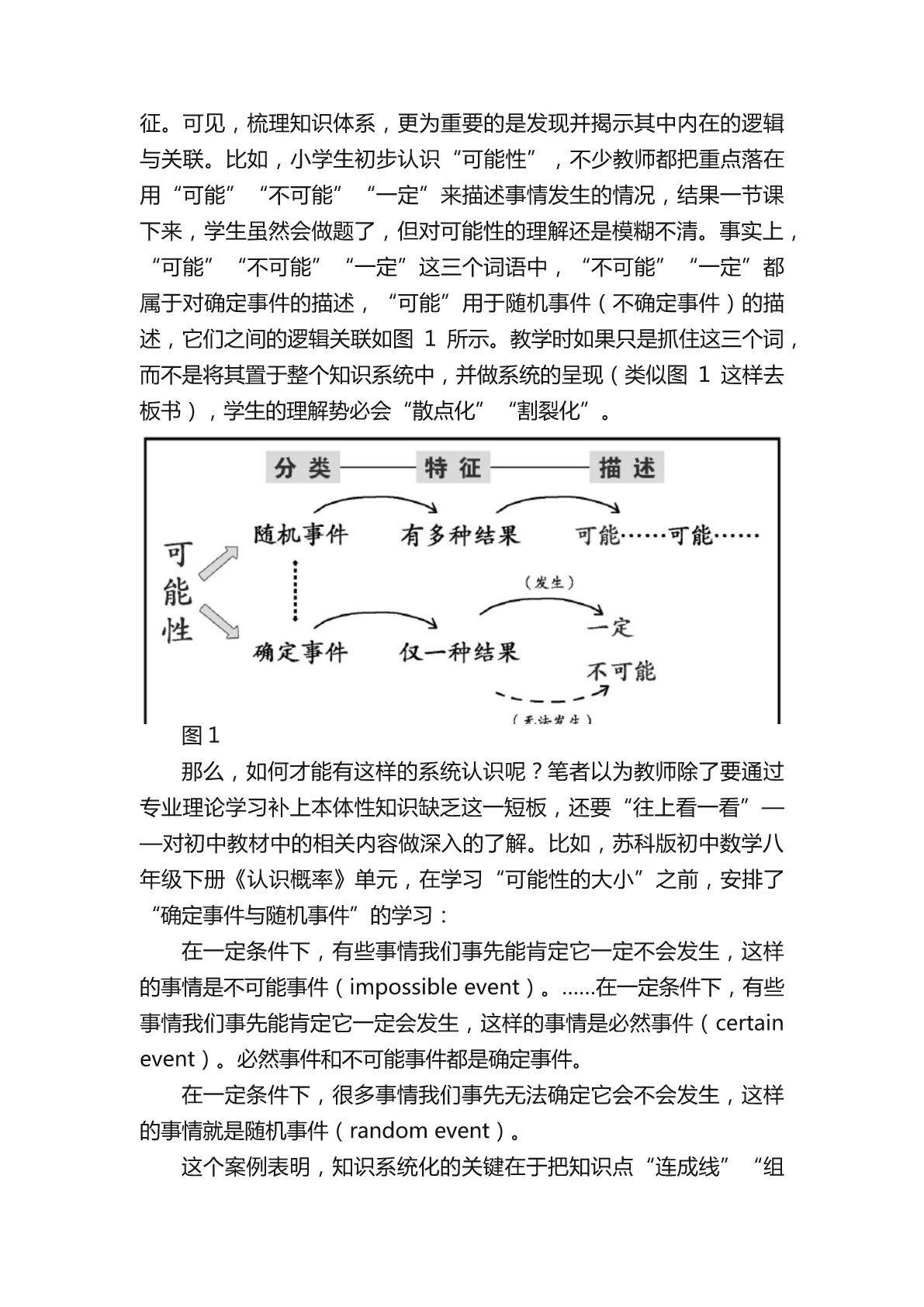
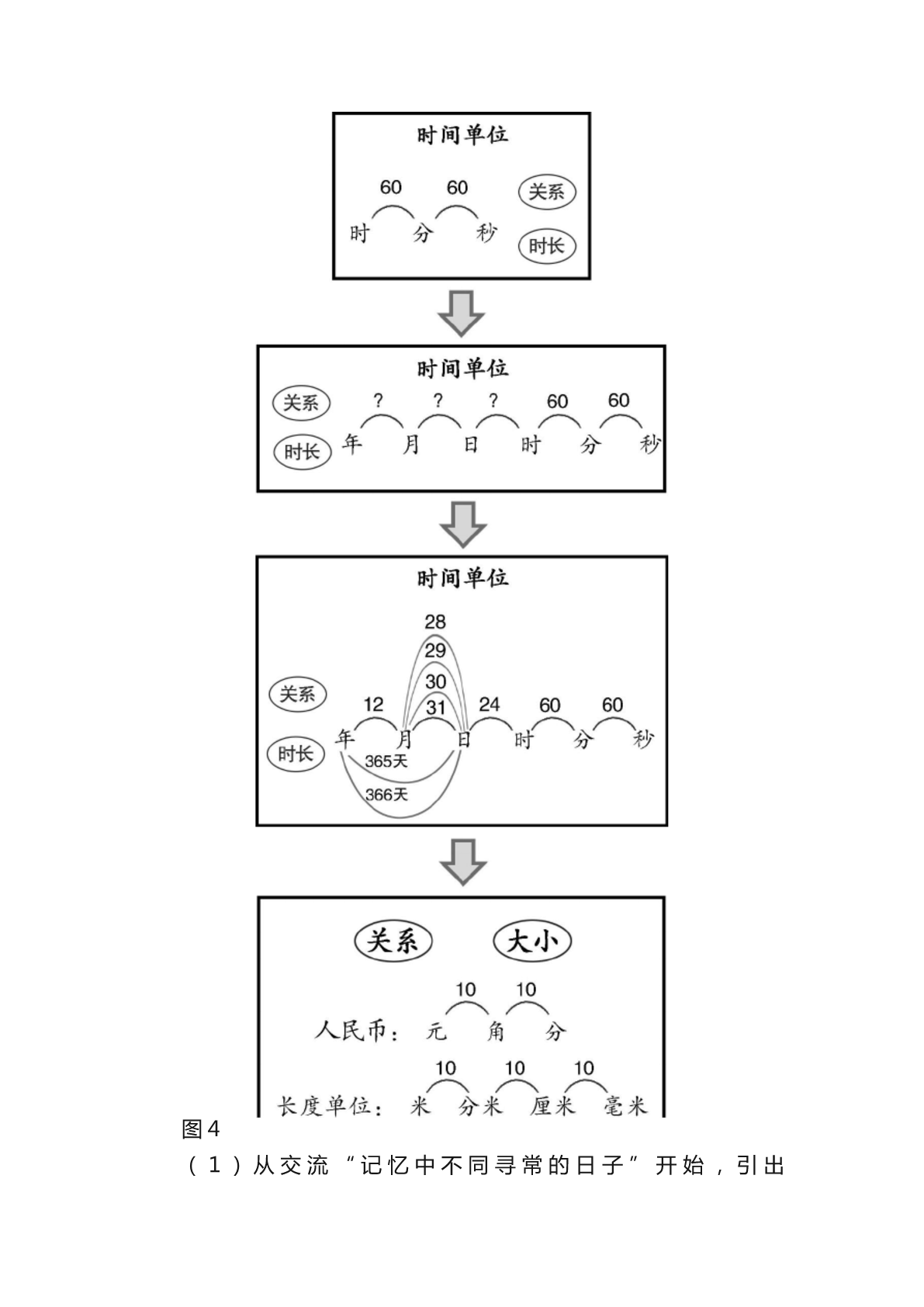
指向整体建构的小学数学教学.pdf

文库****品店








亲,该文档总共16页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

指向整体建构的小学数学教学.pdf
指向整体建构的小学数学教学①许卫兵摘要:整体性、结构性是数学学科的本质特性.用整体建构的理念指导小学数学教学,创建结构化的数学课堂,引领学生在完善认知结构、丰富学习感受、发展思维素养的过程中,逐步地从自主走向自为,符合数学学科的本质,符合儿童数学学习的规律,符合信息时代素养教育的大方向.关键词:整体建构数学教学结构化思维发展046①构活动.或者说,数学的对象并非各个孤立一的模式,而是整体性的‘建构’.”④可见,整关于数学的整体性、结构性,有不少经典体性、结构性是数学学科鲜明的本质特性.论述.瑞士儿童心理学

指向整体建构的小学数学教学.pdf
指向整体建构的小学数学教学欢迎阅读教育研究与评论作者许卫兵,海安市城南实验小学教育集团来源综合版2019年第4期关于数学的整体性、结构性,有不少经典论述。瑞士儿童心理学家皮亚杰早在其1968年出版的《结构主义》一书中就指出:“如果不从检验数学结构开始,就不可能对结构主义进行批判性的陈述。……几乎在所有的数学领域里,并且在逻辑学里,我们都发现了群结构。”美国著名代数学家阿尔贝特说:“数学是结构的科学。当直觉和未经分析的经验表明在许多不同的背景下存在着共同的结构特征时,数学就有了任务,这就是以精确的和客观的形

指向整体建构的小学数学教学.pdf
指向整体建构的小学数学教学欢迎阅读教育研究与评论作者许卫兵,海安市城南实验小学教育集团来源综合版2019年第4期关于数学的整体性、结构性,有不少经典论述。瑞士儿童心理学家皮亚杰早在其1968年出版的《结构主义》一书中就指出:“如果不从检验数学结构开始,就不可能对结构主义进行批判性的陈述。……几乎在所有的数学领域里,并且在逻辑学里,我们都发现了群结构。”美国著名代数学家阿尔贝特说:“数学是结构的科学。当直觉和未经分析的经验表明在许多不同的背景下存在着共同的结构特征时,数学就有了任务,这就是以精确的和客观的形

教学体会-小学数学整体建构教学.pdf
小学数学整体建构教学这本书有五章,我将它分为三个部分:一二章着眼整体;第三章着重联系;四五章着力思考。通过阅读,我对数学的概念,有了新的认识高度,数学是一门“关系”学的表述,数学学习重在培育“关系”思维,以及讨论核心素养要回归到学生身上。所谓“整体建构”,基于数学知识的内在系统关联和学生已有知识基础,通过结构化教学,帮助学生完善认知体系,发展思维能力,培育思维素养,使他们更好地理解、爱上、学好数学,逐步成为学习的主人。之前的教学,“就事论事”课本呈现什么就教什么,练什么,目标性比较强,练习的针对性也很强,

指向深度学习的小学数学单元整体教学.docx
指向深度学习的小学数学单元整体教学看了管老师的报告,边看边截图,感谢管老师分享的公益报告,以下的文字内容来自个人整理,不足之处,敬请批评指正,仅供交流学习。管老师提到现有教材的单元其实就是非常好的整体设计,整体设计要得到良好的效果其关键就在于研究后的实践,同时给各位教师分享了单元整体教学设计的方法,要以不增加课时为底线,设计可多可少,力度可大可小,研究可进可退,程度可深可浅。通过回顾,老师们对单元整体设计有了更深的认识。教材:就是很好的资源,我们真正的去读懂教材,读懂儿童。实际上,小学数学的前世今生紧紧关
