全国统一高考数学试卷(理科)(新课标).pdf

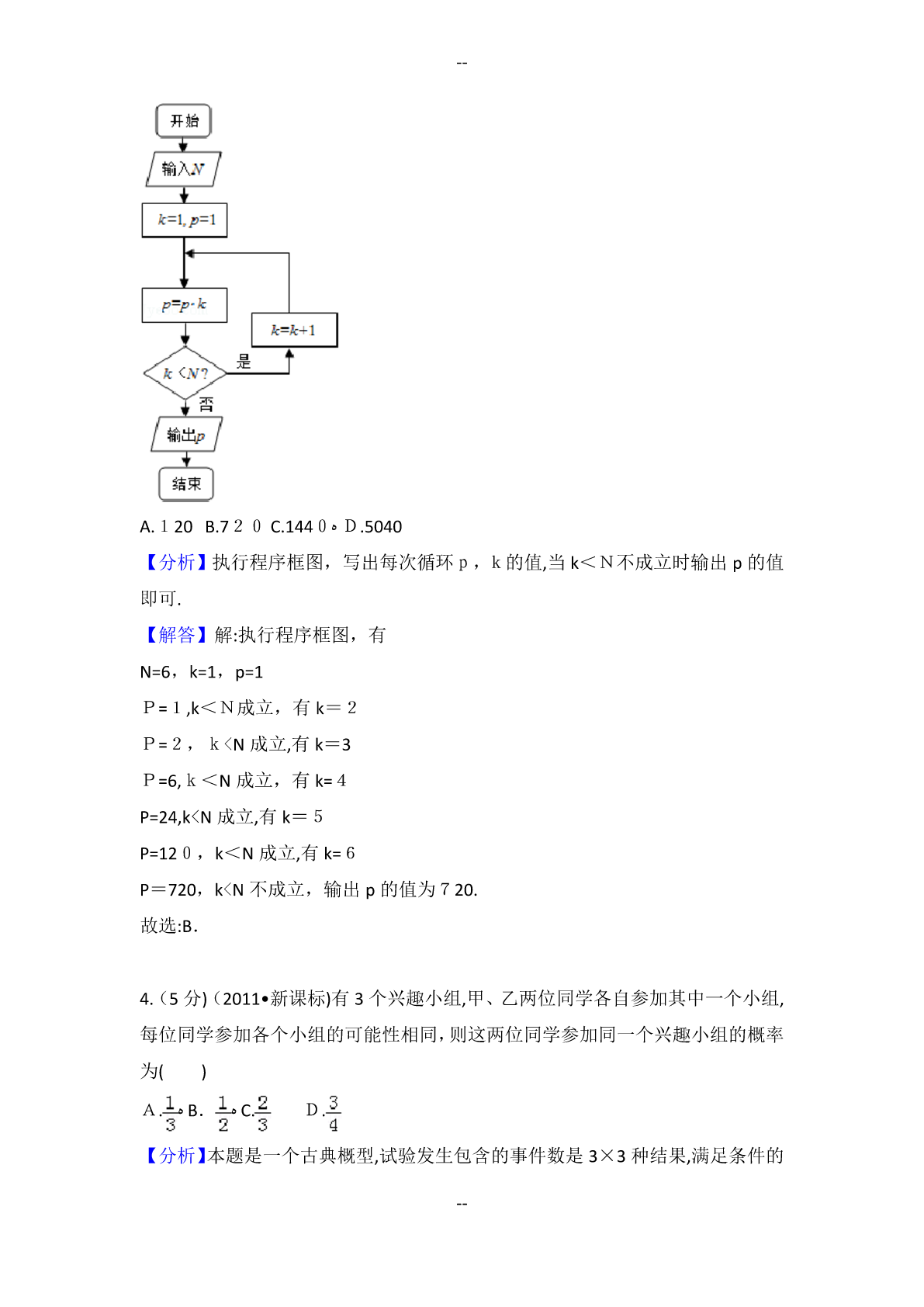
--2011年全国统一高考数学试卷（理科)(新课标)一、选择题（共１2小题，每小题5分，满分６0分)1.（5分）复数的共轭复数是(）A．Ｂ．C．﹣ｉD.i2．(５分)下列函数中,既是偶函数又在(０,+∞)上单调递增的函数是（)｜D．y=2﹣｜ｘﻩＣ．y＝﹣x2＋4ﻩA.y＝2x３B.y=|x｜+１3．(5分)执行如图的程序框图，如果输入的Ｎ是6,那么输出的p是(）D．5０４０ﻩＣ.14４0ﻩA．120B.72０4．(5分）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（）．Dﻩ．Ｃﻩ.A．Ｂ5．(5分)已知角θ的顶点与原点重合，始边与ｘ轴的正半轴重合,终边在直线y＝2x上，则ｃｏs2θ=（)A.﹣Ｂ．﹣Ｃ.D．6.(5分)在一个几何体的三视图中,正视图和俯视图如图所示，则相应的侧视图可----以为（).Ｄﻩ．B.Ｃﻩ．A7.（5分）设直线l过双曲线Ｃ的一个焦点，且与C的一条对称轴垂直，ｌ与C交于Ａ,B两点,|AB|为C的实轴长的2倍,则C的离心率为()C.2Ｄ.3ﻩ.A.B8．(5分）的展开式中各项系数的和为２,则该展开式中常数项为（）D.４0ﻩＣ.20ﻩB.﹣2０ﻩＡ.﹣409.（5分）由曲线y＝,直线y=x﹣2及y轴所围成的图形的面积为(）A.Ｂ．4C.D.６５分已知与均为单位向量，其夹角为，有下列四个命题|+|>１10.()θP1:⇔θ∈[；：|+|>∈（]；Ｐ|﹣|＞∈［，）：0,)P21⇔θ,π3:1⇔θ0;P4|﹣｜＞1⇔θ∈(,π］;其中的真命题是（）D.P，ＰﻩC.Ｐ,PﻩB.P,ＰﻩA.P，P141３２３２４１１.（5分）设函数f（x)=ｓin（ωｘ+φ）＋cｏs(ωx+φ）的最小正周期为π，且f(﹣x）＝f(x)，则（）A.f（x）在单调递减B．f（x)在（,）单调递减D．ｆ（ｘ)在（，)单调递增ﻩＣ.f（x)在（０，)单调递增１2．(5分）函数y＝的图象与函数y＝2siｎπx(﹣2≤ｘ≤4）的图象所有交点的横坐标之和等于(）A.2Ｂ．4C．６D.8----二、填空题（共4小题，每小题5分,满分２0分）１３.（5分)若变量ｘ，y满足约束条件则z＝x+２y的最小值为．（分）在平面直角坐标系ｙ椭圆的中心为原点焦点Ｆ在轴上，14.5xO,C,F12x离心率为．过Ｆ的直线交于A,Ｂ两点，且△ABF的周长为16,那么C的方程l２为.15.(5分）已知矩形ABCD的顶点都在半径为4的球Ｏ的球面上，且AB＝6,BＣ=2，则棱锥O﹣ABCD的体积为．1６.(5分)在△ABC中,B=６０°,ＡＣ＝,则AB+2ＢC的最大值为.三、解答题（共8小题，满分7０分)２1７.(12分)等比数列{ａ}的各项均为正数，且2a+3a=1，ａ=9aａ,ｎ12３26（求数列{}的通项公式；Ⅰ)an（Ⅱ)设b=ｌｏga+loga＋…＋loｇa，求数列{｝的前n项和．ｎ31323n1８.（12分)如图，四棱锥Ｐ﹣ＡBCD中，底面ABＣＤ为平行四边形,∠DＡB=6０°,AB=2AD，ＰＤ⊥底面ＡBCＤ．（Ⅰ）证明:PA⊥ＢＤ；（Ⅱ）若PＤ=AD,求二面角A﹣ＰB﹣C的余弦值．19.（１２分)某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方(分别称为A配方和B配方)做试验，各生产了100件这种产品,并测量了每件产品的质量指标值，得到下面试验结果:A配方的频数分布表指标值分［９0，94）[94,98)[98，102)[１02，10[106，110]----组６）频数82042２28B配方的频数分布表指标值分[９0,94）［94,9８）［98,10２)[10２,106)[106,１1组０］频数41２４２32１0（Ⅰ)分别估计用A配方，Ｂ配方生产的产品的优质品率;（Ⅱ)已知用Ｂ配方生成的一件产品的利润y（单位：元)与其质量指标值ｔ的关系式为ｙ=从用B配方生产的产品中任取一件，其利润记为X（单位:元),求X的分布列及数学期望．（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）20.(１2分)在平面直角坐标系xOy中,已知点A(0，﹣１），Ｂ点在直线y=﹣3上,M点满足∥，=•,Ｍ点的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)P为C上的动点,ｌ为C在P点处的切线，求Ｏ点到l距离的最小值．21.（１２分)已知函数f(ｘ）＝+,曲线y＝f(x）在点（1,f(1））处的切线方程为ｘ+２y﹣３=0．(Ⅰ)求ａ、b的值；(Ⅱ)如果当x>0，且ｘ≠１时，ｆ（x)>+,求k的取值范围.2２.（10分）如图,Ｄ，E分别为△AＢＣ的边AB,AＣ上的点,且不与△ABC的顶点重合．已知AE的长为m,AC的长为n