
MATLAB实现拉格朗插值.pdf

文库****品店







在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

MATLAB实现拉格朗插值.pdf
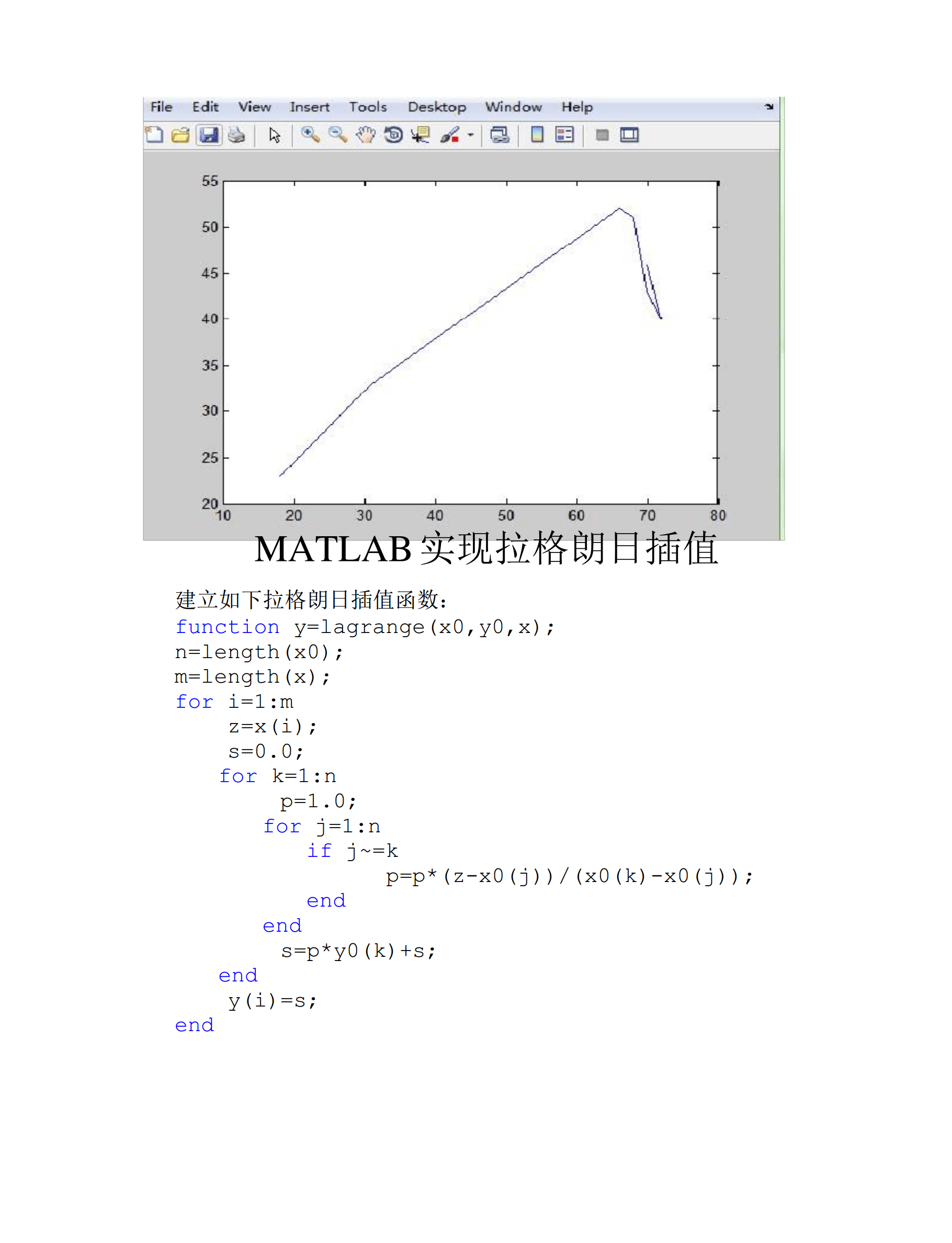
数值分析上机报告题目:插值法学号:202114924姓名:靳会有一、调用MATLAB内带函数插值1、MATLAB内带插值函数列举如下:interp1一维数据内插(查表法)interpft使用FFT方法的一维数据内插interp2二维数据内插(查表法)interp3三维数据内插(查表法)interpn多维数据内插(查表法)spline三次样条内插meshgrid为三维绘图产生X和Y阵ndgrid为多维函数和内插产生阵列griddata数据网格2、取其中的一维数据内插函数〔interp1〕为例,程序如下:其调

MATLAB实现拉格朗日插值.doc
数值分析上机报告题目:插值法学号:201014924姓名:靳会有一、调用MATLAB内带函数插值1、MATLAB内带插值函数列举如下:interp1interpftinterp2interp3interpnsplinemeshgridndgridgriddata一维数据内插(查表法)使用FFT方法的一维数据内插二维数据内插(查表法)三维数据内插(查表法)多维数据内插(查表法)三次样条内插为三维绘图产生X和Y阵为多维函数和内插产生阵列数据网格2、取其中的一维数据内插函数(interp1)为例,程序如下:其调

拉格朗日插值龙格现象的matlab实现.docx
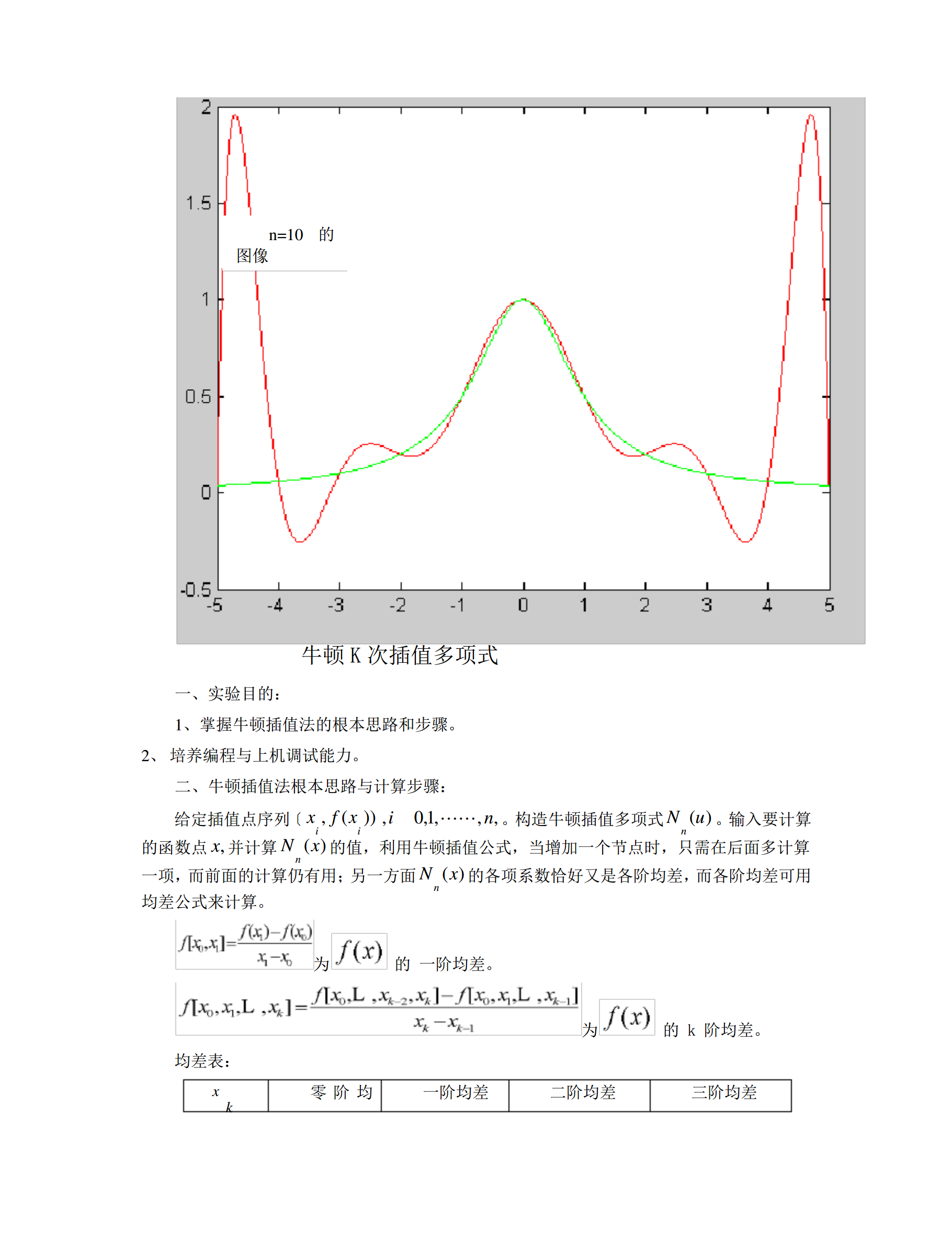
拉格朗日插值龙格现象的MATLAB实现姓名:袁宽学号:201430210065专业:电气工程题目:对于函数,进行拉格朗日插值。,按等距节点求分段线性插值,把和插值多项式的曲线画在同一张图上进行比较。观察Lagrange插值及数值积分中的分段性插值。f.m:functionf=f(x)f=1./(1+x.^2);endLagrange.mfunctiony=Lagrange(x0,y0,x);n=length(x0);m=length(x);fori=1:mz=x(i);s=0.0;fork=1:np=1.

用MATLAB实现拉格朗日插值和分段线性插值.doc
用MATLAB实现拉格朗日插值与分段线性插值1、实验内容:用MATLAB实现拉格朗日插值与分段线性插值。2、实验目得:1)学会使用MATLAB软件;2)会使用MATLAB软件进行拉格朗日插值算法与分段线性差值算法;3、实验原理:利用拉格朗日插值方法进行多项式插值,并将图形显式出来。4、实验步骤及运行结果(1)实现lagrange插值1)定义函数:f=1/(x^2+1)将其保存在f、m文件中,具体程序如下:functiony=f1(x)y=1、/(x、^2+1);2)定义拉格朗日插值函数:将其保存在lagr

用MATLAB实现拉格朗日插值和分段线性插值.doc
用MATLAB实现拉格朗日插值与分段线性插值1、实验内容:用MATLAB实现拉格朗日插值与分段线性插值。2、实验目得:1)学会使用MATLAB软件;2)会使用MATLAB软件进行拉格朗日插值算法与分段线性差值算法;3、实验原理:利用拉格朗日插值方法进行多项式插值,并将图形显式出来。4、实验步骤及运行结果(1)实现lagrange插值1)定义函数:f=1/(x^2+1)将其保存在f、m文件中,具体程序如下:functiony=f1(x)y=1、/(x、^2+1);2)定义拉格朗日插值函数:将其保存在lagr
