时频分析方法综述.pdf

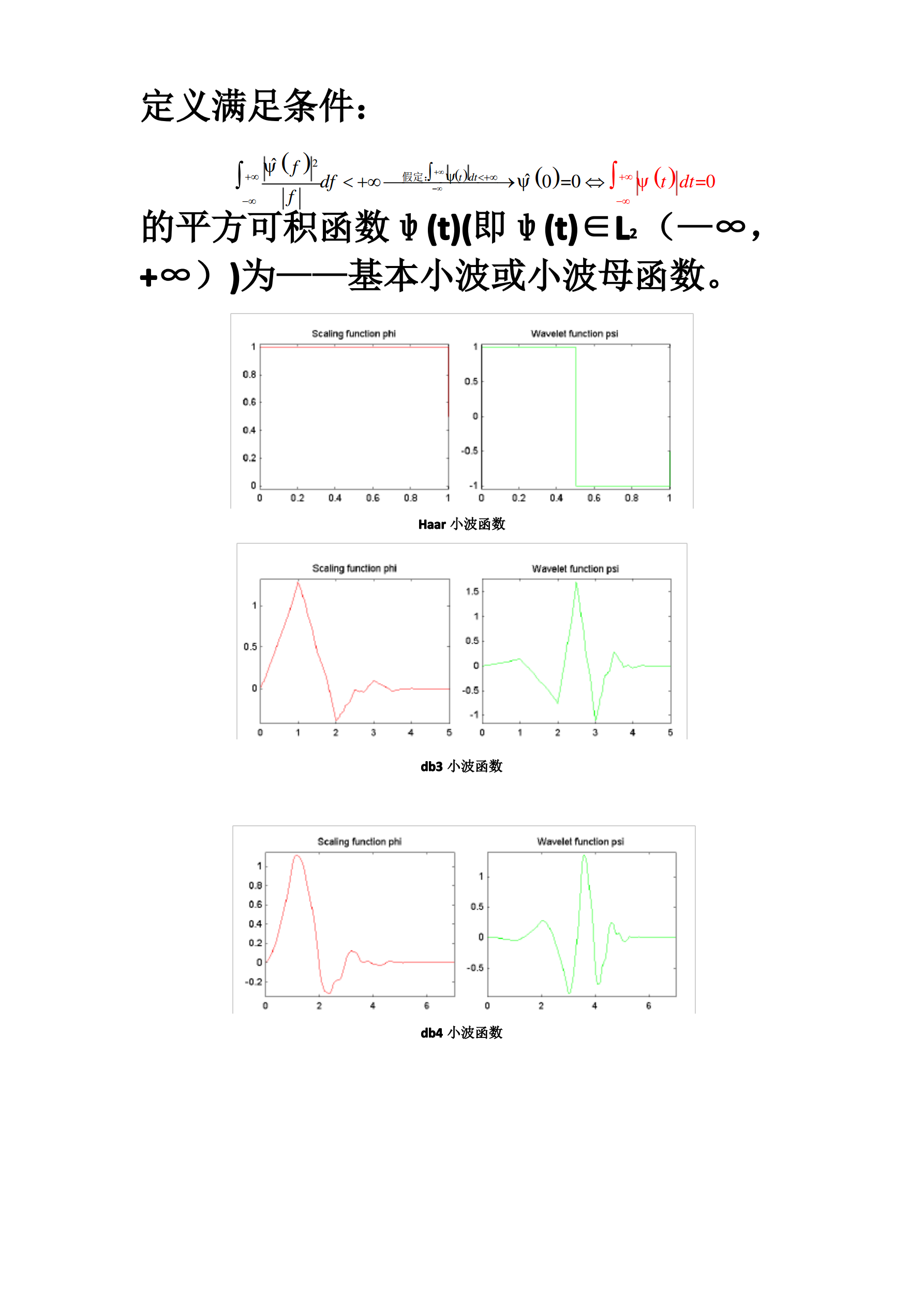
几种时频分析方法简介1．傅里叶变换（FourierTransform）nN1DFT:H()Th(kT)ej2nk/N2ftFT:H(f)h(t)edtNT离散化(离散取样)0周期化（时频域截断）1N1kIFT:h(t)H(f)e2ftdtIDFT:h(nT)H()ej2nk/NNNT02．小波变换（WaveletTransform）a.由傅里叶变换到窗口傅里叶变换（GaborTransform(ShortTimeFourierTransform)/）从傅里叶变换的定义可知，时域函数h(t)的傅里叶变换H(f)只能反映其在整个实轴的性态，不能反映h（t）在特定时间区段内的频率变化情况。如果要考察h(t)在特定时域区间（比如：t∈[a,b]）内的频率成分，很直观的做法是将h(t)在区间t∈[a,b]与函数1,ta,b，然后考察(t)10,ta,b傅里叶变换。但是由于在t=a,bh(t)(t)(t)处突然截断，导致中1出现了原来1h(t)(t)h（t）中不存在的不连续，这样会使得1的傅里叶变化中附件新的高频成h(t)(t)分。1为克服这一缺点，在1944年引入了“窗口”傅里叶变换的概念，他的做法是，取一个光滑的函数g(t),称为窗口函数，它在有限的区间外等于0或者很快地趋于0，然后将窗口函数与h(t)相乘得到的短时时域函数进行FT变换以考察h(t)在特定时域内的频域情况。STFT：G(f,)h(t)g(t)e2ftdtfISTFT：h(t)dfg(t)G(f,)e2ftdf图：STFT示意图STFT算例cos(210t)0st5scos(225t)5st10sx(t)=cos(250t)10st15scos(2100t)15st20s图：四个余弦分量的STFTb.窗口傅里叶变换（Gabor）到小波变换（WaveletTransform）图：小波变换定义满足条件：2ˆf假定：tdtdfˆ0=0tdt=0f的平方可积函数ψ(t)(即ψ(t)∈L2（—∞，+∞）)为——基本小波或小波母函数。Haar小波函数db3小波函数db4小波函数db5小波函数mexh小波函数图：几种常用的小波函数令1tb(t)，a、b为实数，且a≠0，abaa称ψ为由母函数生成的有赖于参数的连续小波函数。设∈2（—∞，∞），定义其aba,bf(t)L+小波变换为：1tbWa,bf,ftdtfabaa与Fourier类似，小波变化也具有反演公式：1dadbftWa,bt，Cfaba2以及Parseval等式：dadbWa,bWa,bCf,g,fga21dadb2Wa,b2ftdt.fCa2小波变换虽然具有频率愈高相应时间或空间分辨率愈高的优点，但其在频率域上的分辨率却相应降低。这是小波变换的弱点，使它只能部分地克服Fourier变换的局限性。小波包变换将在一定程度上弥补小波变换的这一缺陷。图：FT变换、STFT变换及WaveletAnalysis比较图：Wavelet应用1——探测数据突变点图：Wavelet应用1——探测数据突变点（树状显示）图：Wavelet应用2——探测数据整体变化趋势图：Wavelet应用2——探测数据中的频率成分图：Wavelet应用3——压缩数据图：Wavelet应用3——压缩数据3．希尔伯特—黄变换（Hilbert-HuangTransform）希尔伯特与瞬时频率（HilbertTransformandinstantaneousfrequency）对于任意一个时间序列X(t)，它的希尔伯特变换具有如下形式：1X()Y(t)=Pd,-t-其中，P——积分的柯西主值；希尔伯特变换对于任何属于Lp空间中的函数都存立，即上式中X(t)∈Lp（—∞，+∞）。通过上述定义，X(t)和Y(t)成为一组复共轭对，同时能够构造一个实部和虚部分为X(t)和Y(t)的解析信号(AnalyticSignal)Z(t)，Z(t)表示为：Z(t)=X(t)iY(t)=ateit,其中，Y(t)221/2at=X(t)+Y(t),tarctan.X(t)理论上讲有无数种方式去定义虚部，但是希尔伯特变换是唯一能够得到解析信号结果的方法。X(t)的Hilb