
固体导热系数的测定实验报告.pdf

文库****品店




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

固体导热系数测定实验报告.pdf
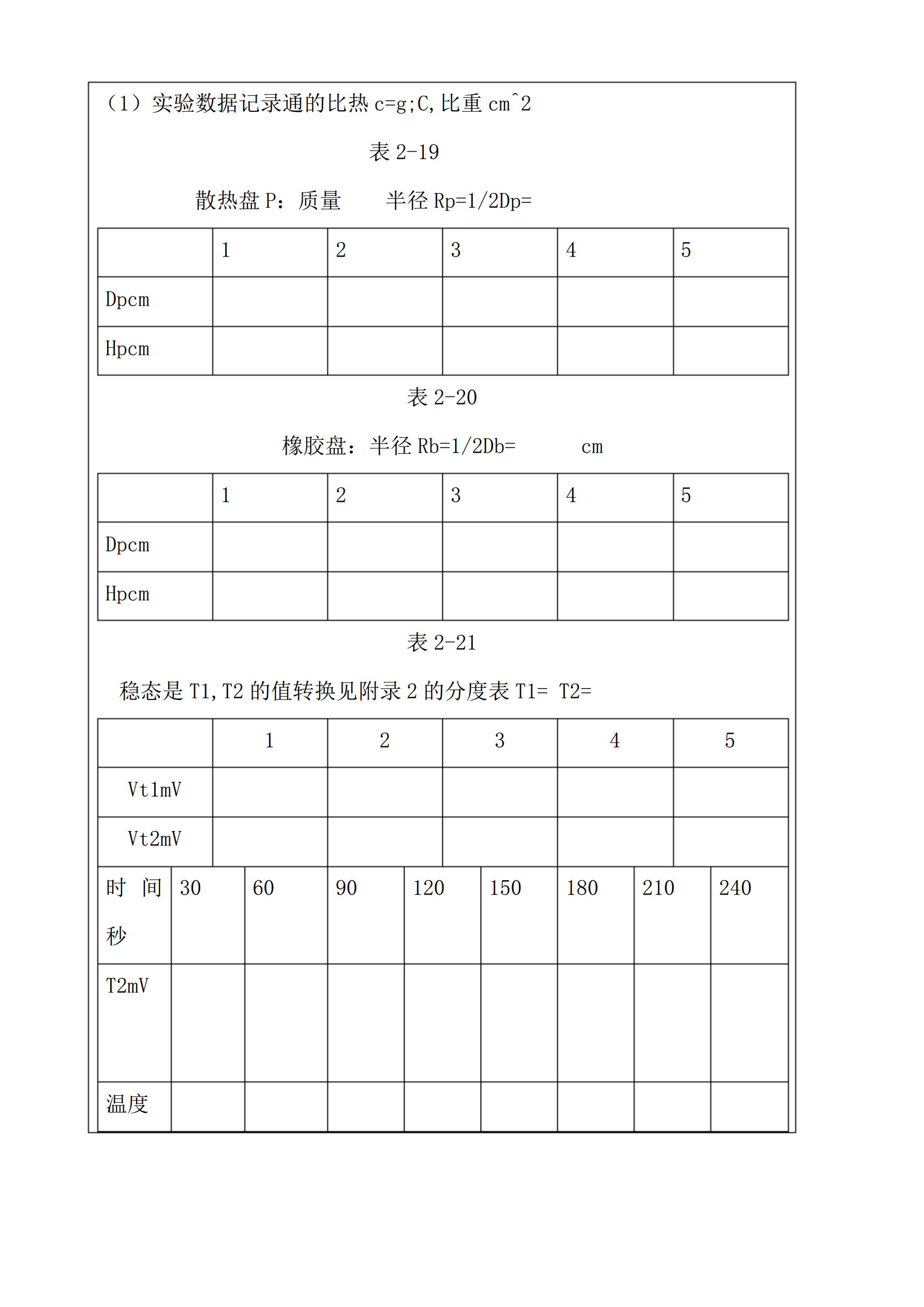
学生物理实验报告实验名称固体导热系数的测定学院专业班级报告人学号同组人学号理论课任课教师实验课指导教师实验日期报告日期实验成绩批改日期实验目的用稳态法测出不良导热体的导热系数,并与理论值进行比较.1/8实验仪器1.数字毫伏表一般量程为20mV。3位半的LED显示,分辨率为10uV左右,具有极性自动转换功能。2.导热系数测量仪一种测量导热系数的仪器,可用稳态发测量不良导体,金属气体的导热系数,散热盘参数2/8实验原理傅里叶在研究了固体的热传定律后,建立了导热定律。他指出,当物体的内部有温度梯度存在时,热量将

固体导热系数的测定实验报告.doc
学生物理实验报告实验名称固体导热系数的测定学院专业班级报告人学号同组人学号理论课任课教师实验课指导教师实验日期报告日期实验成绩批改日期实验目的用稳态法测出不良导热体的导热系数,并与理论值进行比较.实验仪器数字毫伏表一般量程为20mV。3位半的LED显示,分辨率为10uV左右,具有极性自动转换功能。导热系数测量仪一种测量导热系数的仪器,可用稳态发测量不良导体,金属气体的导热系数,散热盘参数实验原理傅里叶在研究了固体的热传定律后,建立了导热定律。他指出,当物体的内部有温度梯度存在时,热量将从高温处传向低温处。

固体导热系数的测定实验报告.doc
学生物理实验报告实验名称固体导热系数的测定学院专业班级报告人学号同组人学号理论课任课教师实验课指导教师实验日期报告日期实验成绩批改日期实验目的用稳态法测出不良导热体的导热系数,并与理论值进行比较.实验仪器数字毫伏表一般量程为20mV。3位半的LED显示,分辨率为10uV左右,具有极性自动转换功能。导热系数测量仪一种测量导热系数的仪器,可用稳态发测量不良导体,金属气体的导热系数,散热盘参数实验原理傅里叶在研究了固体的热传定律后,建立了导热定律。他指出,当物体的内部有温度梯度存在时,热量将从高温处传向低温处。

固体导热系数的测定实验报告.pdf
学生物理实验报告实验名称固体导热系数的测定学院专业班级报告人学号同组人学号理论课任课教师实验课指导教师实验日期报告日期实验成绩批改日期实验目的用稳态法测出不良导热体的导热系数,并与理论值进行比较.实验仪器1.数字毫伏表一般量程为20mV;3位半的LED显示,分辨率为10uV左右,具有极性自动转换功能;2.导热系数测量仪一种测量导热系数的仪器,可用稳态发测量不良导体,金属气体的导热系数,散热盘参数实验原理傅里叶在研究了固体的热传定律后,建立了导热定律;他指出,当物体的内部有温度梯度存在时,热量将从高温处传向

固体导热系数的测定实验报告.pdf
固体导热系数的测定实验报告--学生物理实验报告实验名称固体导热系数的测定学院专业班级报告人学号同组人学号理论课任课教师实验课指导教师实验日期报告日期实验成绩批改日期实验目的用稳态法测出不良导热体的导热系数,并与理论值进行比较.实验仪器1.数字毫伏表一般量程为20mV。3位半的LED显示,分辨率为10uV左右,具有极性自动转换功能。2.导热系数测量仪一种测量导热系数的仪器,可用稳态发测量不良导体,金属气体的导热系数,散热盘参数固体导热系数的测定实验报告--固体导热系数的测定实验报告--实验原理傅里叶在研究了
