标准椭圆形封头的几何形状.doc

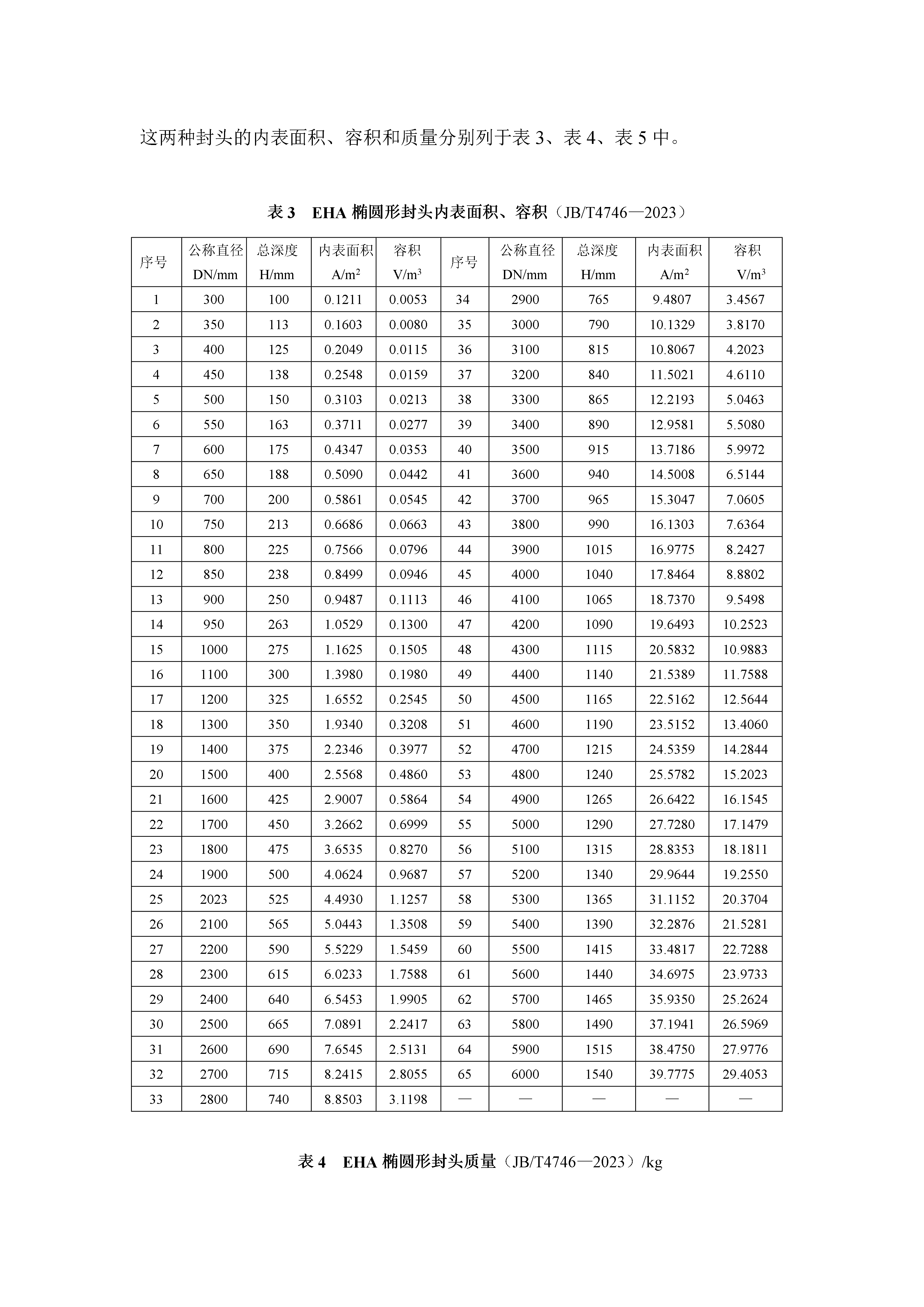
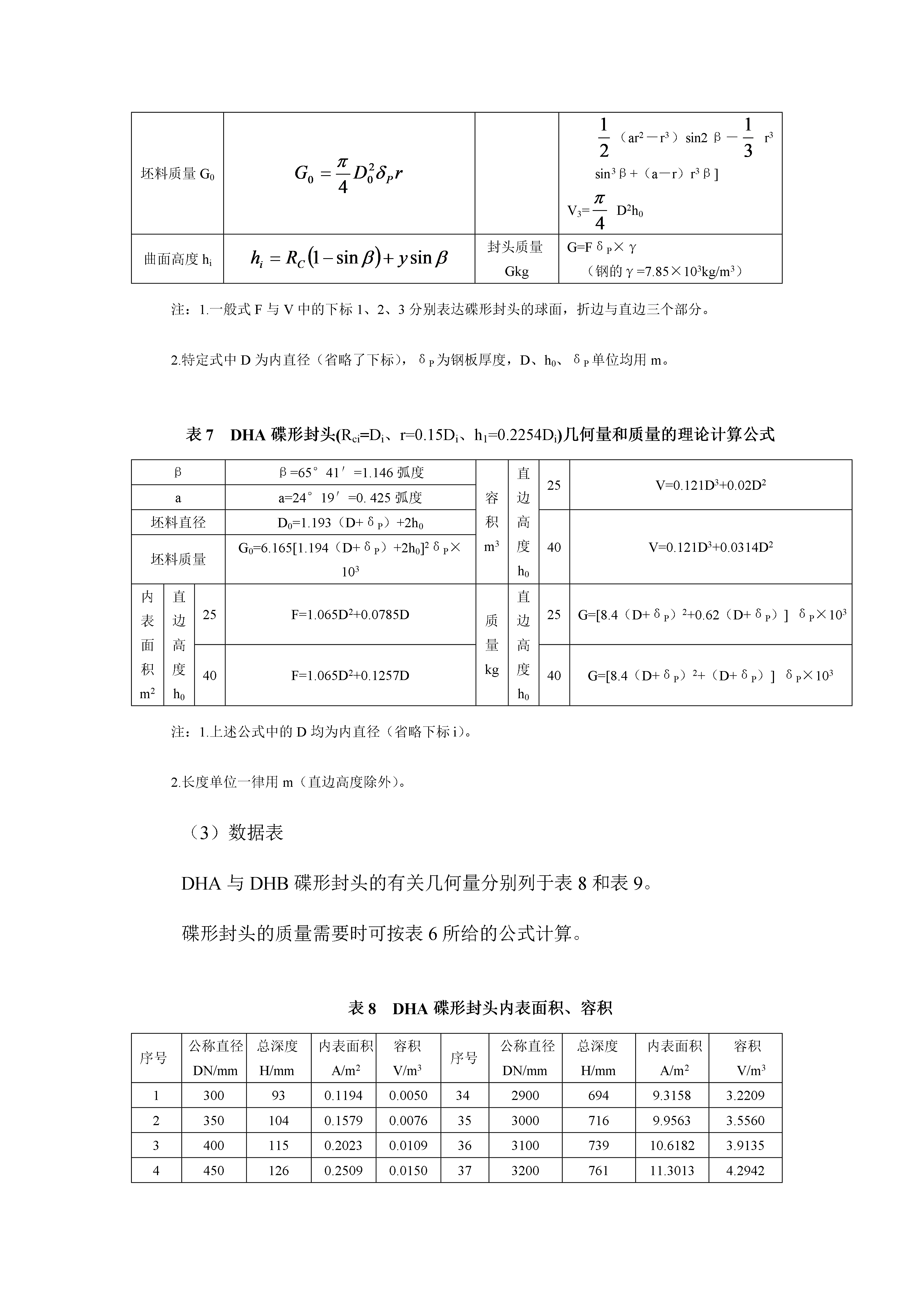
标准椭圆形封头的几何形状、尺寸和质量（1）封头的几何形状形成这种封头的母线是由1/4椭圆线和一条平行于回转轴的短直线光滑连接而成，因而这种封头是由半个椭球和一个高度为h0的圆柱形短节（称它为封头的直边部分）构成。标准椭圆形封头的曲面深度h1与封头公称直径之比为1比4。直边高度按封头的公称直径推荐两种尺寸：当封头公称直径DN小于、等于2023mm时，h0=25mm；当封头公称直径DN大于2023mm时，h0=40mm。（2）封头几何量与质量的计算公式椭圆形封头的几何量与质量的计算公式与四个参数有关，即：长轴半径a，短轴半径b，直边高度h0和钢板厚度δP，其计算式列于下表1：表1椭圆形封头的几何量与质量的通用计算公式坯料直径坯料质量内中或外表面积容积质量注：1.式中长度单位一律用m，钢板密度单位为kg/m3。2.根据需要a、b可按封头内径，中径或外径取值。3.对于以内径为公称直径的标准椭圆形封头，其有关计算公式列下表2。根据表1所列公式，对于任何a、b值的椭圆形封头均可算出其有关各几何量及质量的数值。表2标准椭圆形封头的几何量与质量计算公式项目计算公式坯料直径D0坯料质量G0内表面积Fi容积V封头质量G注：1.以上各式均按a=0.5Di,b=0.25Di,按表2通用计算公式导出。2.封头质量公式应按封头中面计算，表中G式曲面部分是按封头外表面计算的。对于以内径为公称直径的封头，其中的Fi和V，可用a=0.5Di和b=0.25Di,代入表1中各式，但对D0、G0和G应以中面为基础，为了计算公式简朴，表2中的D0、G0，G式均以外表面作为计算基础（直边部分除外），且作了不影响工程上允许精确度的简化。对于以外径为公称直径的封头，表1中的F和V应当用a=0.5DH－δP和b=0.25DH－δP代入，对于G应先算出封头中面面积，这时a=0.5DH－0.5δP，b=0.25DH－0.5δP。假如将上述值代入表2有关公式后，得到的计算公式较为繁琐，所以不再给出。（3）数据表根据JB/T4746—2023《钢制压力容器用封头》的规定，以内径为基准的标准椭圆形封头形式代号为EHA，以外径为基准的椭圆形封头形式代号为EHB，这两种封头的内表面积、容积和质量分别列于表3、表4、表5中。表3EHA椭圆形封头内表面积、容积（JB/T4746—2023）序号公称直径DN/mm总深度H/mm内表面积A/m2容积V/m3序号公称直径DN/mm总深度H/mm内表面积A/m2容积V/m313001000.12110.00533429007659.48073.456723501130.16030.008035300079010.13293.817034001250.20490.011536310081510.80674.202344501380.25480.015937320084011.50214.611055001500.31030.021338330086512.21935.046365501630.37110.027739340089012.95815.508076001750.43470.035340350091513.71865.997286501880.50900.044241360094014.50086.514497002000.58610.054542370096515.30477.0605107502130.66860.066343380099016.13037.6364118002250.75660.0796443900101516.97758.2427128502380.84990.0946454000104017.84648.8802139002500.94870.1113464100106518.73709.5498149502631.05290.1300474200109019.649310.25231510002751.16250.1505484300111520.583210.98831611003001.39800.1980494400114021.538911.75881712003251.65520.2545504500116522.516212.56441813003501.93400.3208514600119023.515213.40601914003752.23460.3977524700121524.535914.28442015004002.55680.4860534800124025.578215.20232116004252.90070.5864544900126526.642216.15452217004503.26620.6999555000129027.728017.14792318004753.6535