
南京市旅游景区景点系统空间结构分形研究.pdf

文库****品店





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

南京市旅游景区景点系统空间结构分形研究.pdf
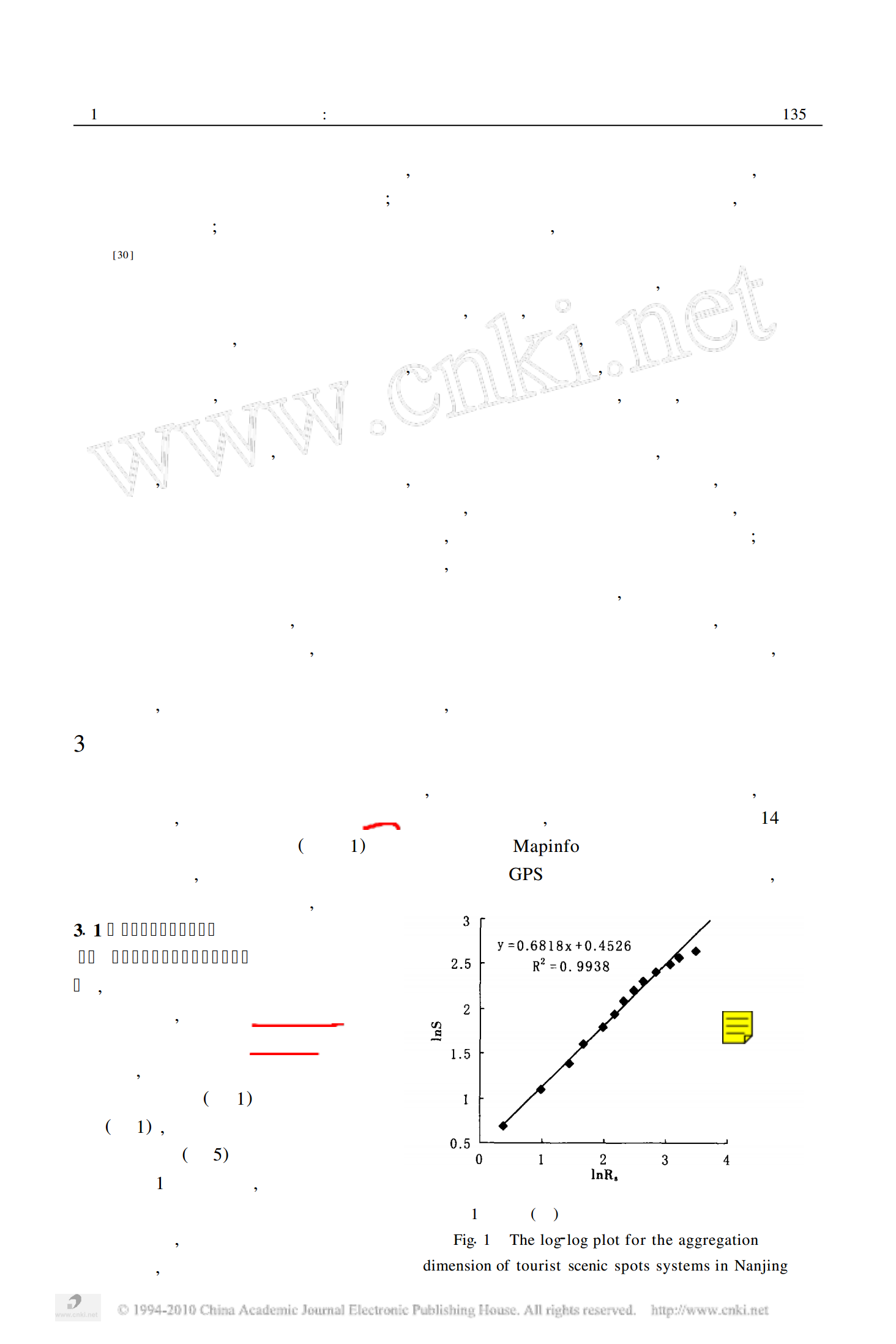
26卷第1期地理研究Vol126,No112007年1月GEOGRAPHICALRESEARCHJan1,2007南京市旅游景区景点系统空间结构分形研究许志晖1,戴学军2,庄大昌3,林岚4,丁登山1(11南京大学城市与资源学系,江苏南京210093;21惠州学院经管系,广东惠州516007;31广东商学院旅游与环境学院,广东广州510320;41福建师范大学地理科学学院,福建福州350007)摘要:应用分形理论,以南京市旅游景区景点系统为例,测算出其聚集维数、网格信息维数和空间关联维数三种分形维数,对景区

南京市旅游景区景点系统空间结构分形研究.pdf
26卷第1期地理研究Vol126,No112007年1月GEOGRAPHICALRESEARCHJan1,2007南京市旅游景区景点系统空间结构分形研究许志晖1,戴学军2,庄大昌3,林岚4,丁登山1(11南京大学城市与资源学系,江苏南京210093;21惠州学院经管系,广东惠州516007;31广东商学院旅游与环境学院,广东广州510320;41福建师范大学地理科学学院,福建福州350007)摘要:应用分形理论,以南京市旅游景区景点系统为例,测算出其聚集维数、网格信息维数和空间关联维数三种分形维数,对景区

旅游景区(点)系统空间结构网格分形维数研究.docx
旅游景区(点)系统空间结构网格分形维数研究旅游景区(点)系统空间结构网格分形维数研究一、前言随着旅游业的发展,越来越多的人开始关注旅游景区(点)的空间结构问题。其中,网格分形维数是一个重要的参数,可以帮助我们深入了解景区(点)的空间特点,进而优化景区(点)的规划和设计。本文将探讨旅游景区(点)系统的空间结构网格分形维数研究。二、什么是网格分形维数网格分形维数是计算机科学领域的一个技术概念。它指的是一个图形的细节程度,也就是说,计算网格分形维数可以帮助我们了解一个图形的复杂程度。网格分形维数的计算方法比较复

鄂西生态文化旅游圈景区空间结构分形研究.docx
鄂西生态文化旅游圈景区空间结构分形研究鄂西地区是我国山西省西南部的一个地理区域,因其独特的生态环境和丰富的人文资源而吸引了大量的游客前来观光旅游。随着旅游业的不断发展,鄂西地区的旅游业也呈现出了快速增长的态势。为了更好地发掘和利用这一地区的旅游资源,需要对鄂西地区的旅游景区空间结构进行研究分析。本文主要研究鄂西生态文化旅游圈景区空间结构的分形特征和优化方案。一、鄂西生态文化旅游圈景区空间结构分析1、景区空间结构的特征鄂西生态文化旅游圈景区的空间结构主要由景区的地理位置、景区内的交通方式、景区内的建筑、景观

福建省旅游景区(点)空间结构分形研究--以主要旅游景区(点)为例的中期报告.docx
福建省旅游景区(点)空间结构分形研究--以主要旅游景区(点)为例的中期报告中期报告一、研究背景和意义福建省境内旅游资源丰富,旅游业发展迅速。但是,不同旅游景区之间的空间结构差异较大,且大多数研究主要关注旅游景区的定量分析,而忽略了对旅游景区空间结构的研究。因此,对福建省旅游景区(点)空间结构进行分形研究,不仅有助于深入了解福建省旅游景区(点)的空间特征,还可以为旅游规划和管理提供科学依据。二、研究目标和方法本研究旨在探究福建省主要旅游景区(点)的空间结构分形特征,具体目标如下:1.探究福建省主要旅游景区(
