奥赛典型例题分析(振动和波).ppt

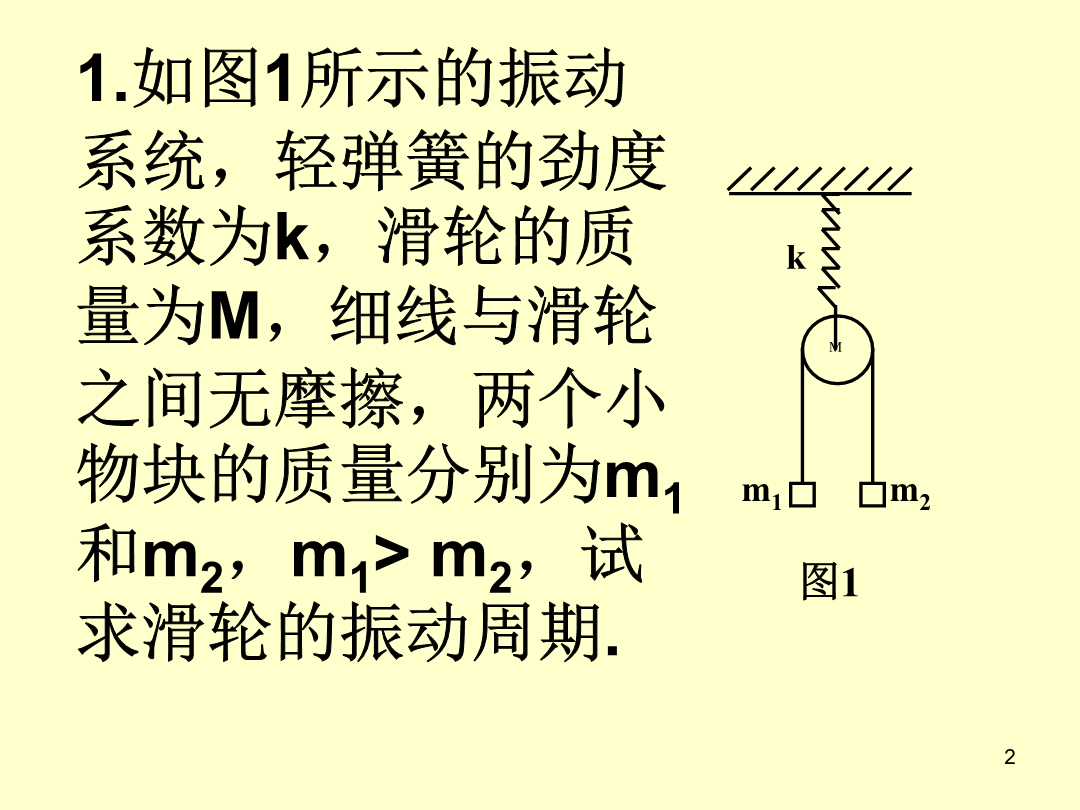
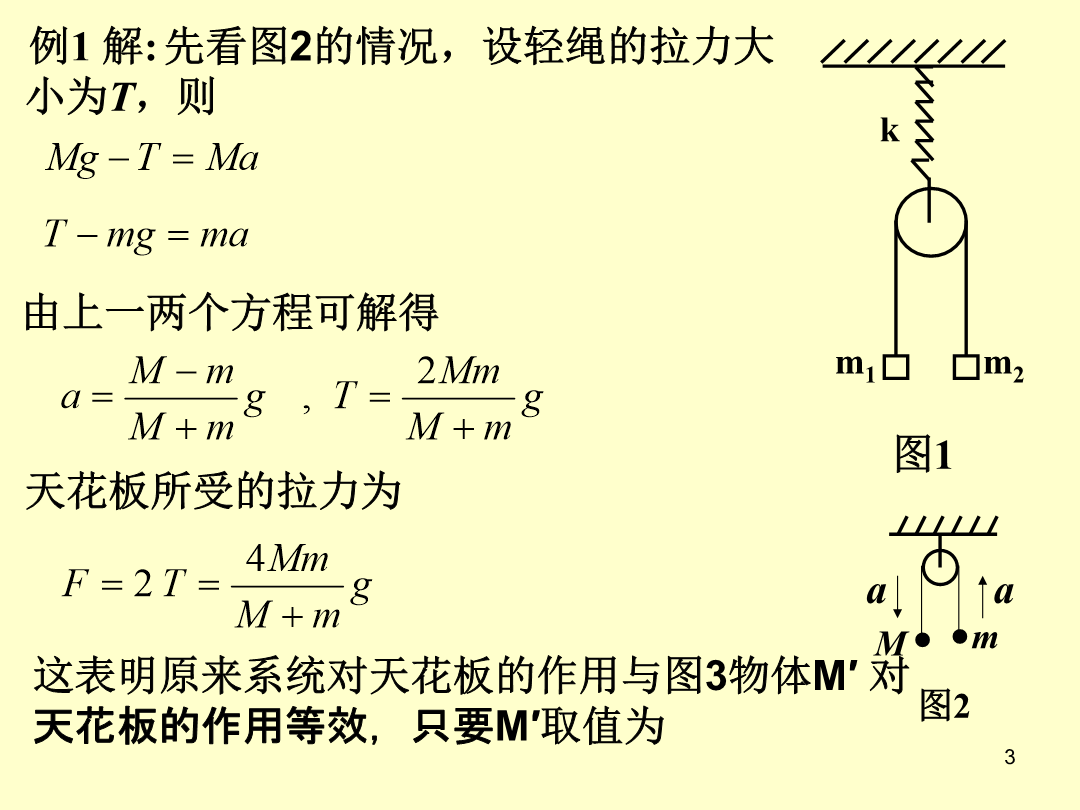
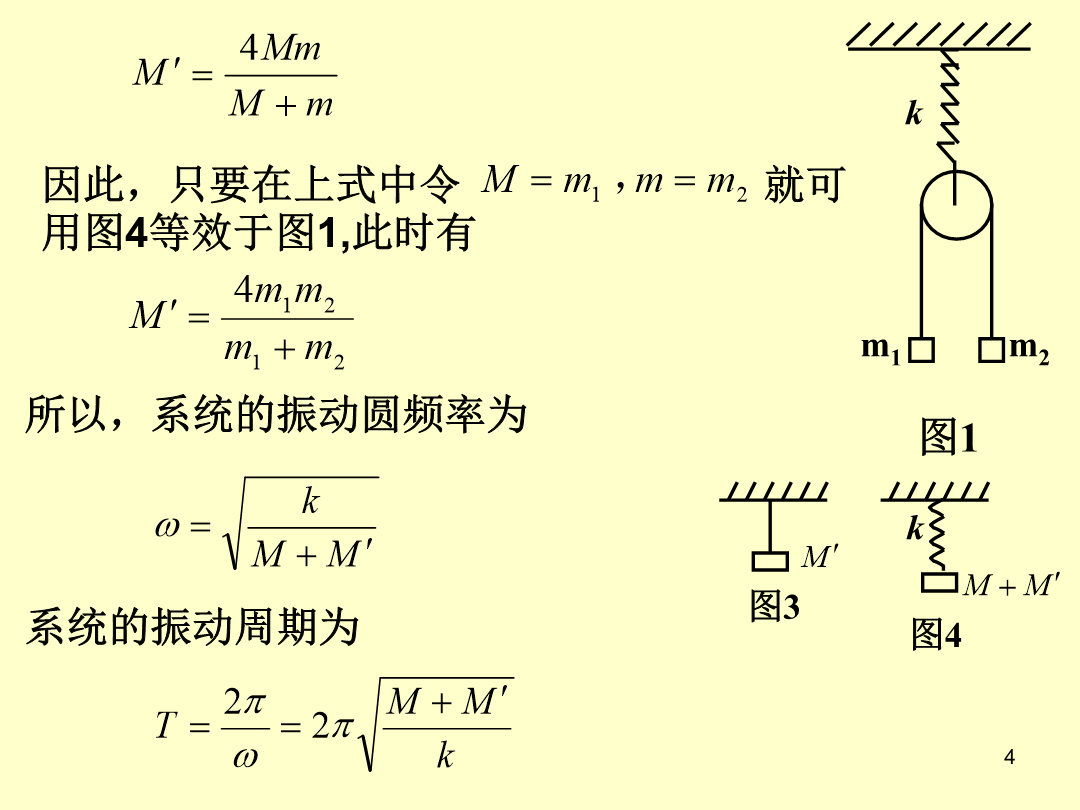
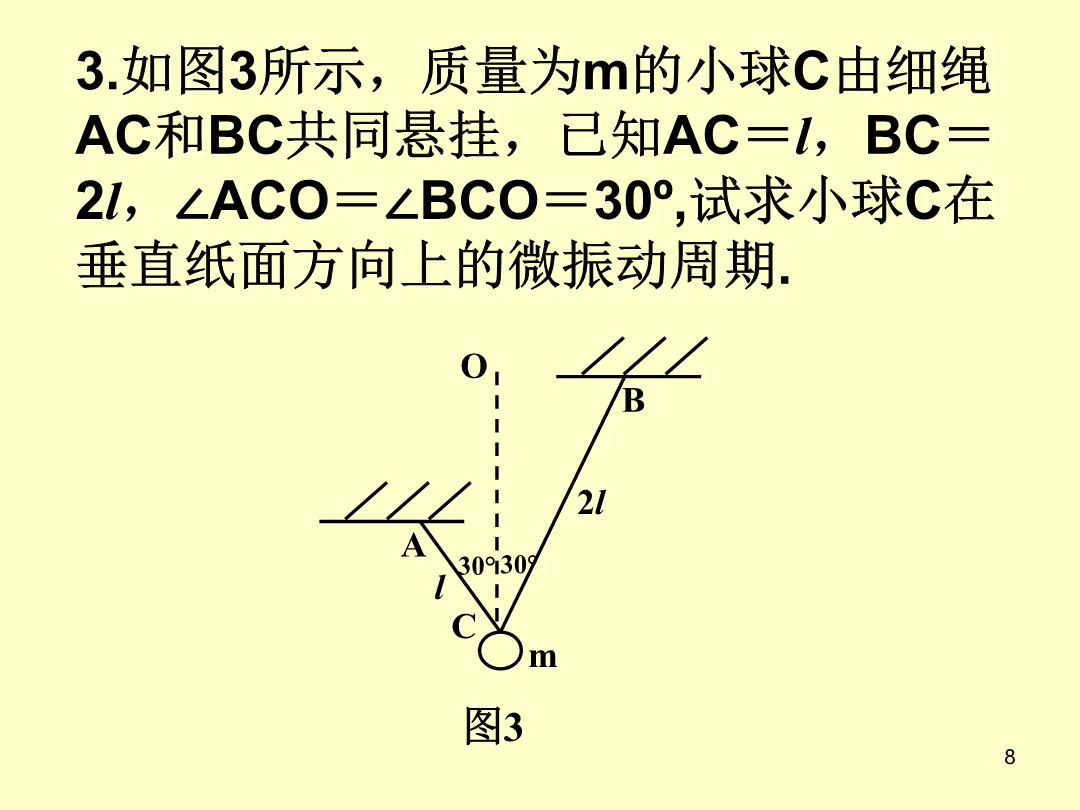
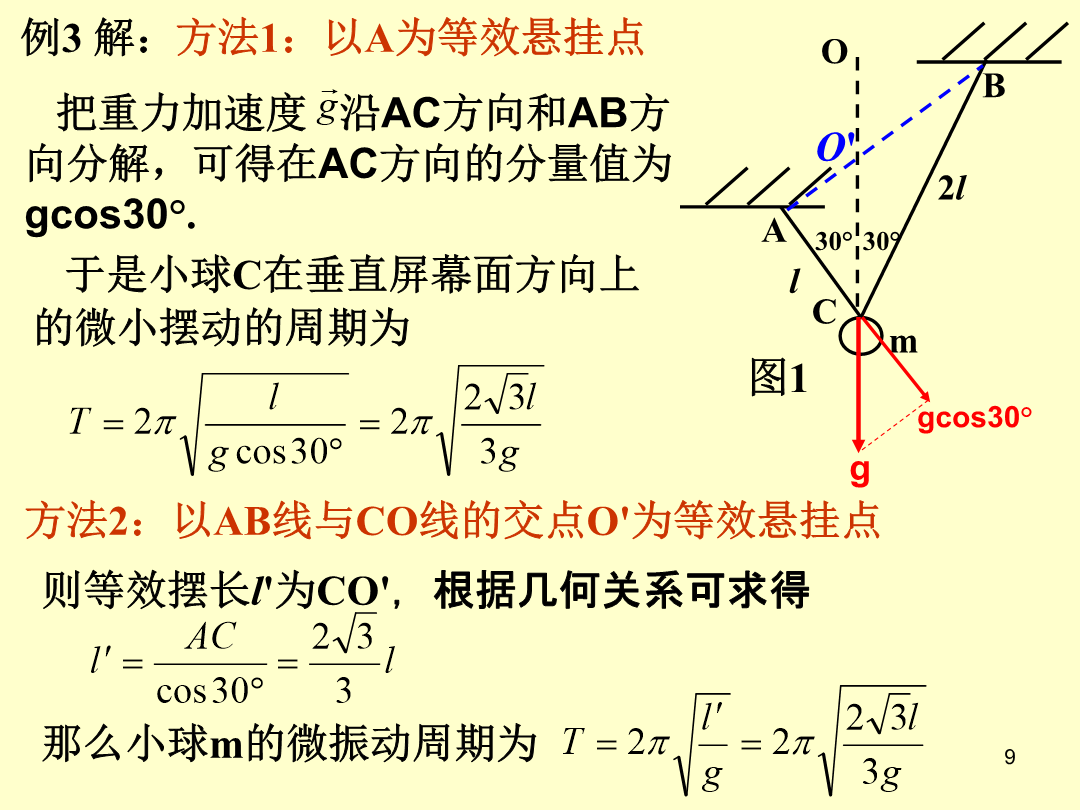
奥赛典型例题1.如图1所示的振动系统，轻弹簧的劲度系数为k，滑轮的质量为M，细线与滑轮之间无摩擦，两个小物块的质量分别为m1和m2，m1>m2，试求滑轮的振动周期.例1解:图32.如图2所示，物体的质量为m，用弹簧悬挂吊于水平轻杆上，杆的一端与光滑铰链相连，另一端用弹簧悬挂，已知k1、k2、m及尺寸a、b，试求物体m的振动周期.设当m处于平衡位置时，弹簧1、2的伸长量分别为∆l10和∆l20,则由(5)、(6)式可得3.如图3所示，质量为m的小球C由细绳AC和BC共同悬挂，已知AC＝l，BC＝2l，∠ACO＝∠BCO＝30º,试求小球C在垂直纸面方向上的微振动周期.方法1：以A为等效悬挂点4.半径为R的轻圆环上固定两个质量相同的小重物，在环上与两个小重物距离相等的O处钻一小孔，将这小孔穿过墙壁上的光滑小钉而把圆环挂起来，使圆环可以在竖直平面上作微振动，两小重物的位置关系可以用它们之间的角距离2α表示，如图4所示，试求圆环微振动的周期.例4解：C5.如图5所示，在水平光滑桌面的中心有一个光滑小孔O，一条劲度系数为k的细弹性绳穿过小孔O，绳的一端系于小孔O正下方地面的A处，另一端系一质量为m的小物块，弹性绳的自然长度等于OA，现将小物块沿桌面拉至B点处，OB＝L，并给小物块一个与OB垂直的初速度v0沿桌面射出，试求：(1)小物块绕O点转过90°到达C点所需要的时间;(2)小物块到达C点时的速度及CO的长度.例5解：质点从起始位置B绕O点运动到C点，对于x方向的简谐振动来说，质点是从最大位移的位置运动到平衡位置的，恰好经历了1/4T,所以可求得6.三根长为l＝2.00m的质量均匀的直杆构成一个等边三角形框架ABC，C点悬挂在一光滑水平转轴上，整个框架可绕转轴转动，杆AB是一导轨，一电动玩具松鼠可在导轨上运动，如图6所示，现观测到松鼠正在导轨上运动而框架却静止不动，试证明松鼠的运动应是一种什么样的运动.例6解：由此可见，玩具松鼠的运动必然是简谐振动.7.A是某种材料制成的小球，B是某种材料制成的均匀刚性薄球壳，假设A与B的碰撞是完全弹性的，B与桌面的碰撞是完全非弹性的.已知球壳质量为m，内半径为r，放置在水平无弹性的桌面上，小球A的质量也为m，通过一自然长度为r的柔软弹性绳悬挂在球壳内壁的最高处，且有kr=9mg/2，k为弹性绳的弹性系数.起初将小球A拉到球壳的最低点，如图7所示，然后轻轻释放，试详细地、定量地讨论小球A以后的运动.(92年第9届预赛题)例7解：所以小球的振幅为所以这表明小球A将与球壳相碰，由于两者质量相等，且碰撞为弹性碰撞，所以，A与B交换速度，B竖直上抛，而小球A则自由下落.B能上升的最大高度为令，其中故由图2所示的参考圆可知，小球A从O点下落再回到O点需时间为此后，球壳B一直保持静止，而小球A则作简谐振动→竖直上抛运动→简谐振动→竖直上抛运动→简谐振动…这样的周期性运动，其运动周期为8.如图8所示，一只狼沿半径为R的圆形岛边缘按逆时针方向匀速跑动，当狼经过岛边缘某点时，一只猎犬以相同速率v从岛中心O出发追赶狼，设在追赶过程中狼、猎犬、中心O三者始终在同一直线上，问猎犬应沿何种曲线追赶？它在何处可以追上狼？例8解：方法一（解析法）：图1图1方法二：猜想和证明法设犬到达D点时狼到达C点，连接犬的轨迹圆的圆心O'和D点，因圆心角是对应的弦切角的两倍，所以，∠DO'O=2θ.9.到了晚上，地面辐射降温使空气层中产生温度梯度，温度随高度递增，这导致声速v随高度y变化，假定变化规律为v=v0(1+a2y2)，其中v0是地面（y＝0）处的声速，a为比例常数，今远方地面上某声源发出一束声波，发射方向与竖直方向成角，假定在波的传播范围内ay<<1，试求该声波在空间传播的轨迹，并求地面上听得最清楚的地点与声源的距离.例9解：由于声速沿y轴递增，折射角也逐渐增大，也即各层的入射角逐渐增大，到某一层入射角超过了临界角时，声波就会发生全反射而折回地面.由于中学未教积分，故采用下面方法来得到y与x的关系式.于是有，ω值尚待定.由(6)式可见，在温度随高度y依题设条件递增的空气中向上传播的声波为一正弦曲线，声波传播的轨迹曲线与x轴的交点就是声波沿波线上扬下弯后重返地面处，此处闻声清楚，此处坐标满足：