建筑制图总复习.ppt

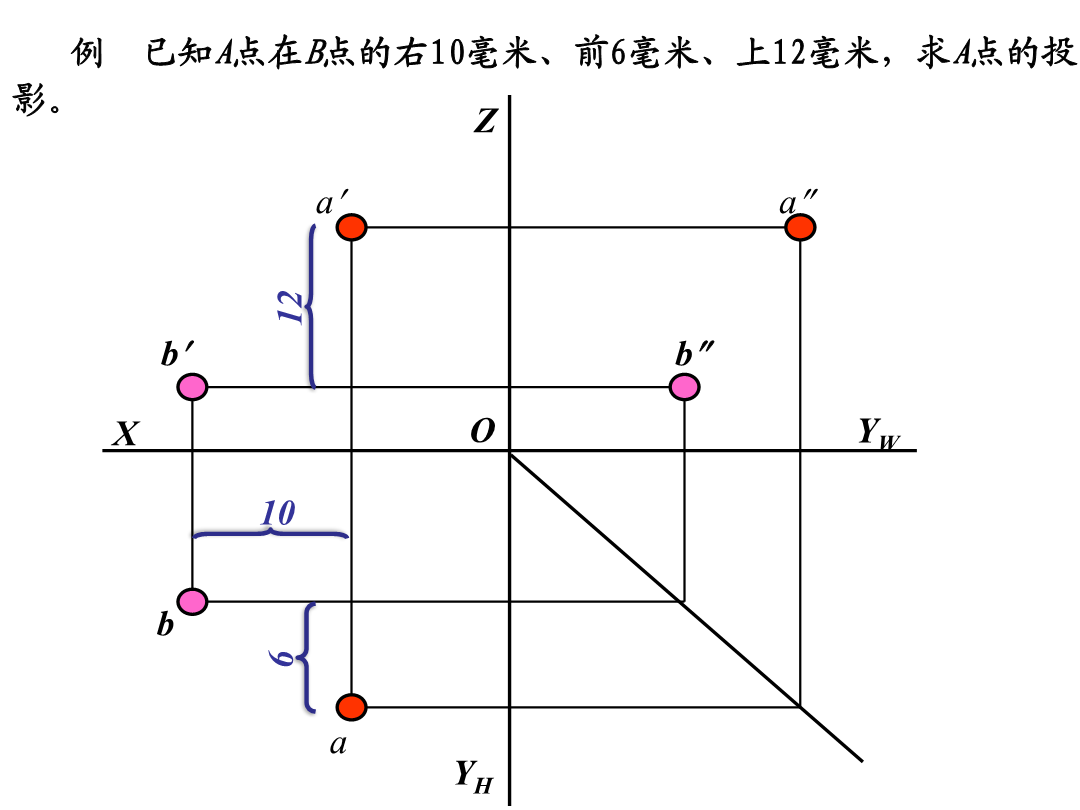
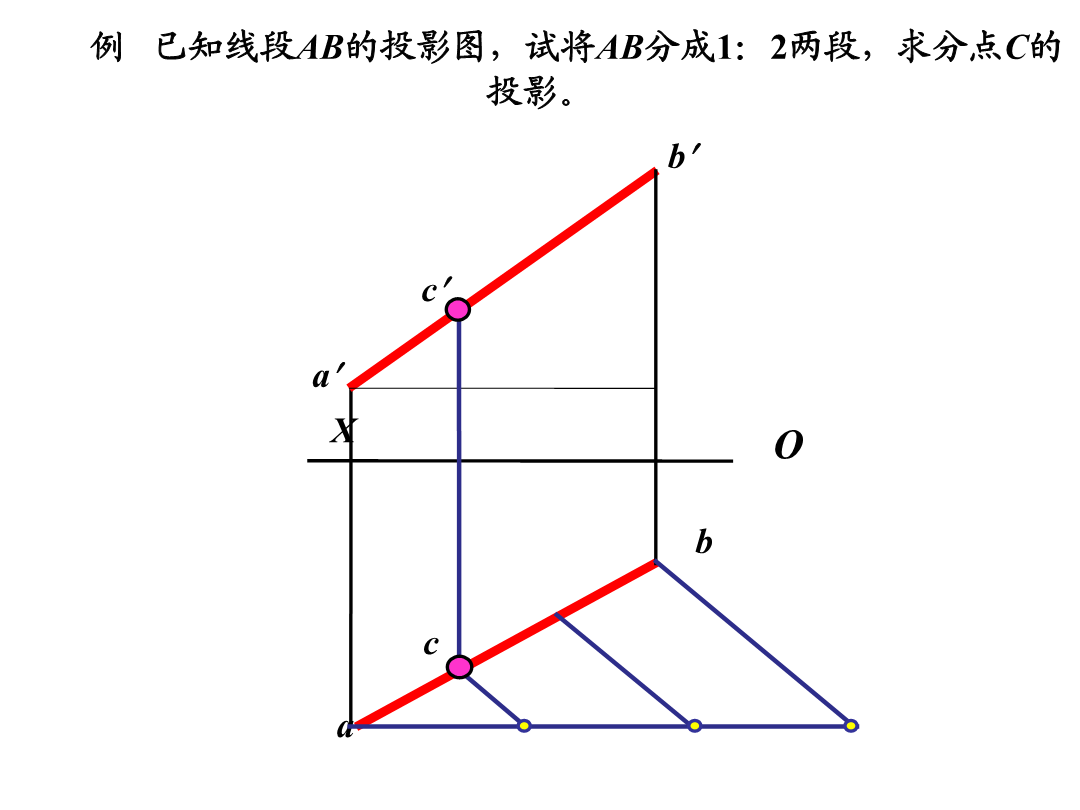
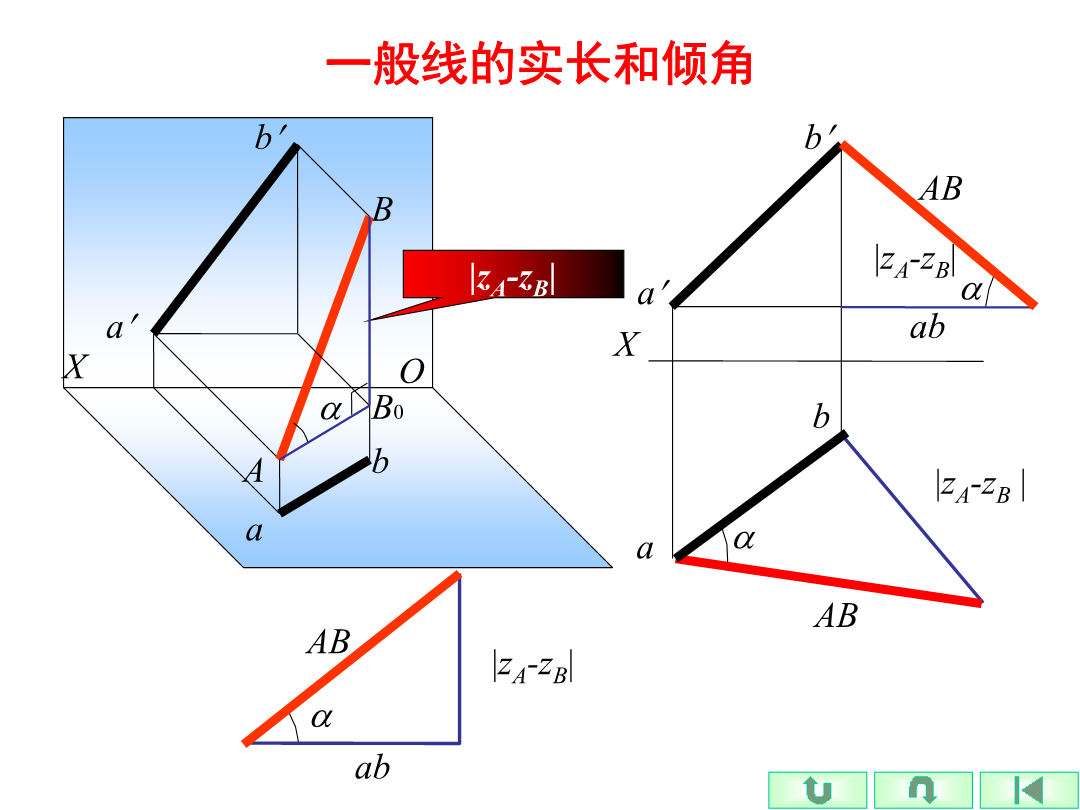
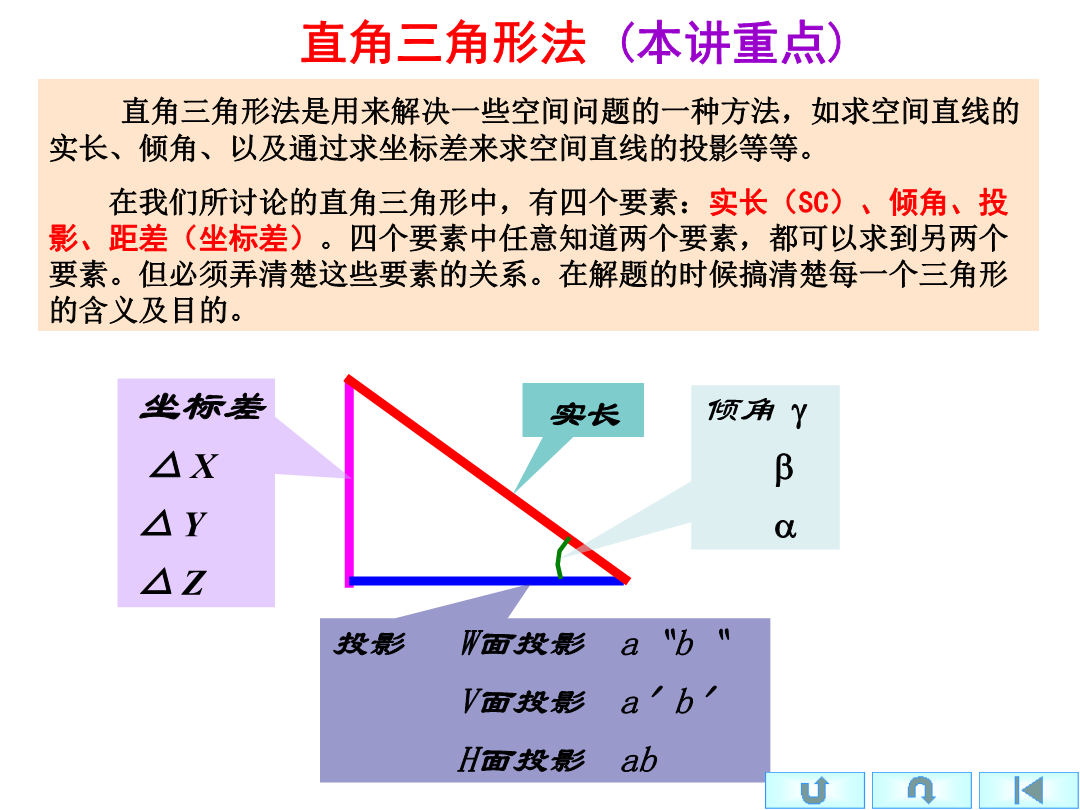
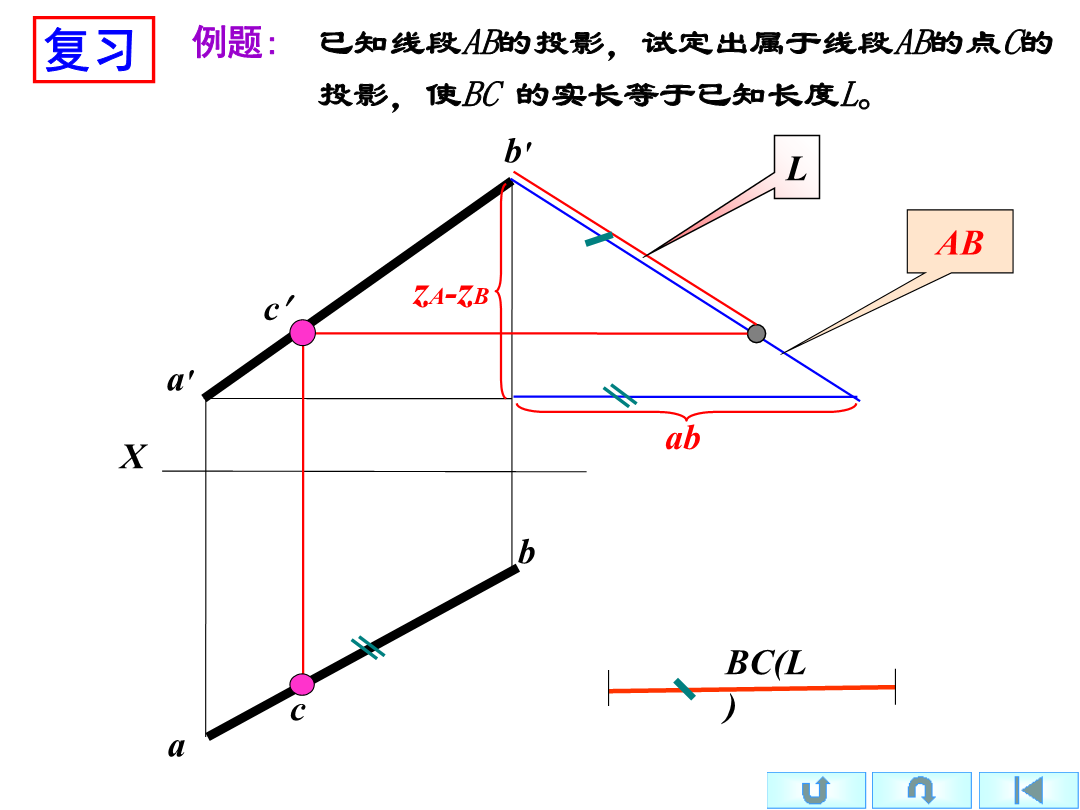
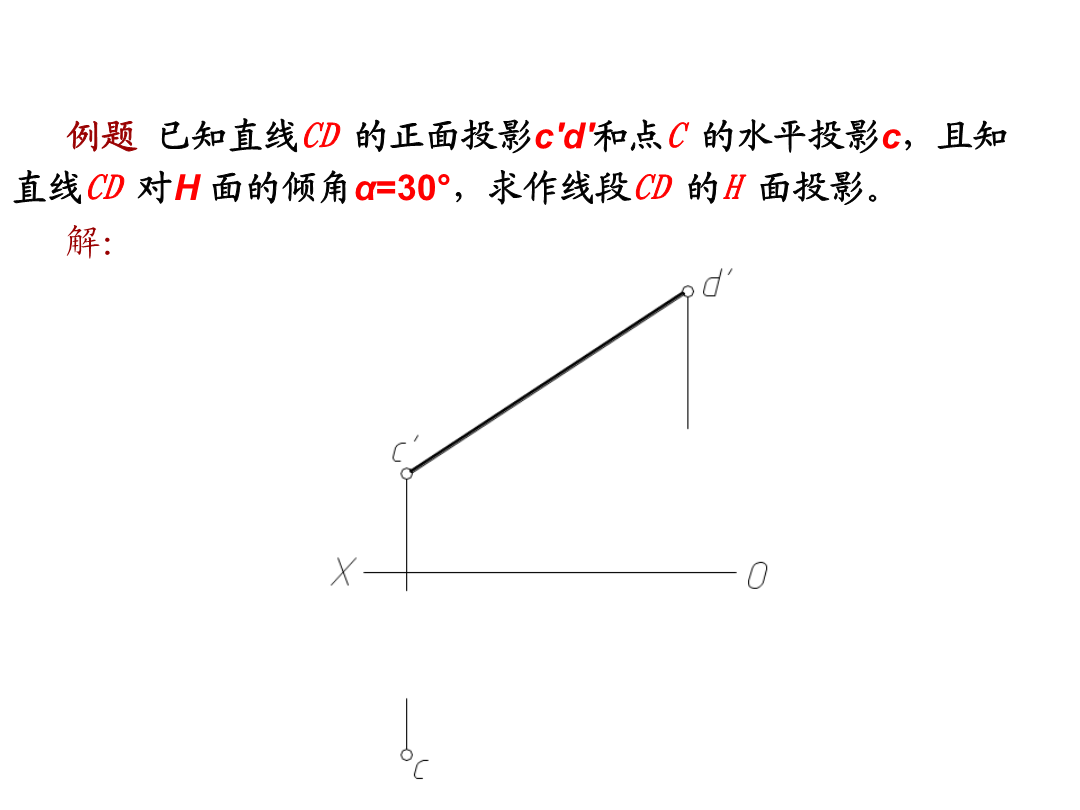
《建筑制图》总复习一、点的投影例已知A点在B点的右10毫米、前6毫米、上12毫米，求A点的投影。二、直线的投影b直角三角形法(本讲重点)b例题已知直线CD的正面投影c'd'和点C的水平投影c，且知直线CD对H面的倾角α=30°，求作线段CD的H面投影。解：3.两直线的相对位置:平行、相交、交叉b练习册P92-17直线的迹点如果空间二直线垂直，且一直线是某一投影面的平行线，则该面投影仍反映垂直。如果二直线在某投影面上反映垂直，且其中一直线是该面的平行线，则空间二直线垂直。相叉垂直的两直线的投影d解题的关键点:求另一对角线BD的正投影长(用直角三角形法);ac=AC=BDbd已知3.求出∣ZD-ZE︱=∣ZE-ZB∣或求d′b′(e′d′或e′b′)b练习册P72-14练习册P72-18三、平面的投影（1）两平行直线在同一投影面上的投影仍平行。反之，若两直线在同一投影面上的投影相互平行，则该两直线平行。（2）平行两线段之比等于其投影之比。2.相交两直线3.交错两直线例例2例题例题(1)最大斜度线:平面上对某个投影面倾角最大的直线。(2)它与投影面的倾角反映该平面与投影面的倾角。(3)平面内对某投影面的最大斜度线与该平面内某投影面的平行线相互垂直。(4)作图步骤：①在平面内作一平行线②用直角定理作一直线垂直于平行线③用所作的最大斜度线求倾角（直角三角形法）最大斜度线对投影面的角度最大。最大斜度线的几何意义:用来测定平面对投影面的角度例题复习题1：已知点E在△ABC平面上，且点E在B点的前方15、B点的下方10，试求点E的投影。已知BC为正平线，完成平面四边形ABCD的水平投影。四、直线与平面、平面与平面的相对位置1.直线与平面、平面与平面平行小结复习题:已知定平面由平行两直线AB和CD给定。试过点K作一平面平行于已知平面。一般位置线面相交由于直线和平面的投影都没有积聚性，求交点时无积聚性投影可以利用，因此通常要采用辅助平面法求一般位置线面的交点。一般位置线、面相交求交点的步骤：（l）含已知直线作特殊位置的辅助平面；（2）求辅助平面与已知平面的交线；（3）求交线与已知直线的交点，交点即为所求。4.2.1积聚性法直线可见性的判别X（2）两平面相交平面可见性的判别交线是直线一般线与一般面相交(本讲重点)过AB作平面P垂直于H投影面2f1利用求一般位置线面交点的方法找出交线上的两个点，将其连线即为两平面的交线。1、用直线与平面求交点的方法求出两平面的两个共有点K、L。利用重影点判别可见性例7试过K点作一直线平行于已知平面ΔABC，并与直线EF相交。分析作图步骤五、平面立体平面与平面立体相交解题步骤：先视截交线是积聚元素上的线，立即得到一个投影，立即标点，标点后在多边形投影上得到交线的另一投影。利用点在直线上、点在平面上的方法在第三投影上求出截交线上各点的第三投影。连点成封闭的图形（按其余二投影的顺序）整理图形：根据积聚投影所在的投影来保留剩下部分（没参加相交的部分）习题6-17：完成带缺口三棱柱的H、W投影。习题6-15：作出六棱锥被P、Q平面截割后的投影。直线与立体表面的交点称为贯穿点。贯穿点是直线与立体表面的公有点（既是属于直线的点，又是属于立体表面的点）。因此，求贯穿点的问题，就是求线与面交点的问题。求贯穿点的方法：包含已知直线作一个辅助截平面，求此截平面与立体的截交线，截交线与已知直线的交点即为贯穿点。例题：求直线KL与三棱锥的贯穿点。K作图过程：120°仰视与俯视例题：画出形体的正等测图。P193图13-7P195图113-11