圆周角定理及推论1.ppt

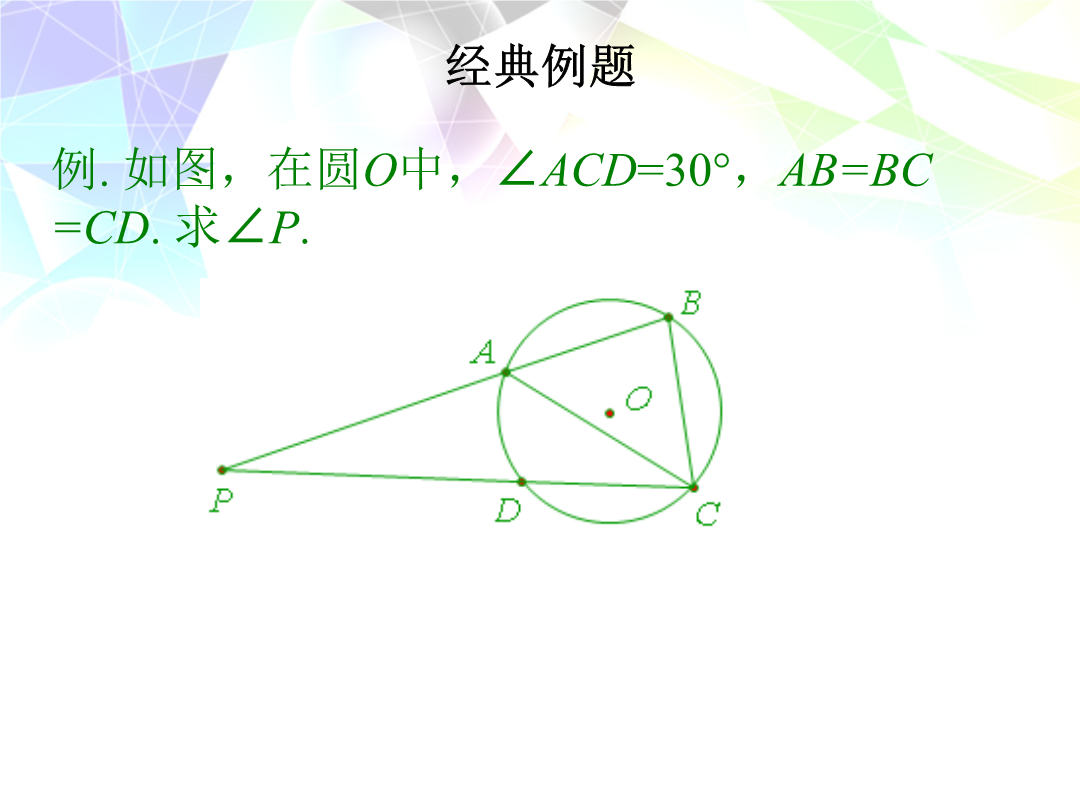
第二十七章圆经典例题巩固练习巩固练习提高练习拓展练习回味无穷课后作业冯康刚进初中时，英语遇到困难，由于他在小学一点英语也未学过，而其他同学大多学过英语.问题之解决完全靠他自己的努力，很快就跟上了班，不仅如此，还跃居班上的前列.整个这段时期之内，他是轻松愉快地进行学习，而不是中国传统教育强调的苦学，也从来不开夜车（这和他后来的情况完全不同），即使考试时期，亦是如此.至于数学，不仅课堂学习成绩优异，他还参考原版的范氏大代数等国外教本进行学习和解题，应该说他中学数学根底非常扎实.还有值得一提的是，有一本科普著作对他产生的深远影响，就是朱言钧著的“数理丛谈”.朱言钧（朱公谨）是我国前辈数学家，曾在哥廷根大学留学，回国后在上海交大任教.这本书是通过学者和商人的对话来介绍什么是现代数学（其中也提到费马大定理、哥德巴赫等问题），这本书有很强的感染力，使冯康眼界大开，首次窥见了现代数学的神奇世界，深深为之入迷.这也许是冯康献身数学立志成为数学家的一个契机.当然，道路并不是笔直的.——冯康的故事