微积分课件专题培训市公开课一等奖百校联赛特等奖课件-豆柴文库

微积分课件专题培训市公开课一等奖百校联赛特等奖课件.pptx

2024-02-10

10金币

2.4MB

98页

胜利****实阿

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共98页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

微积分ppt课件专题培训市公开课一等奖百校联赛特等奖课件.pptx

定积分计算法则、性质积分基本法则函数与常数乘积积分证函数之和积分证积分是线性对积分区间可加性几何意义积分非负性积分非负性几何意义保序性保序性几何解释有界性有界性－几何解释（1/5）有界性－几何解释（2/5）有界性－几何解释（3/5）有界性－几何解释（4/5）有界性－几何解释（5/5）积分绝对值不等式证积分中值定理定积分中值定理从数平均值到函数均值从数平均值到函数均值在下式中一个做法：将[a,b]等分为n个小区间，将分点作为求均值x_i,则由函数均值函数均值基本性质（已知）证使积分中值定理注积分是一个求和练

2024-02-13

1.5MB

微积分课件专题培训市公开课一等奖百校联赛特等奖课件.pptx

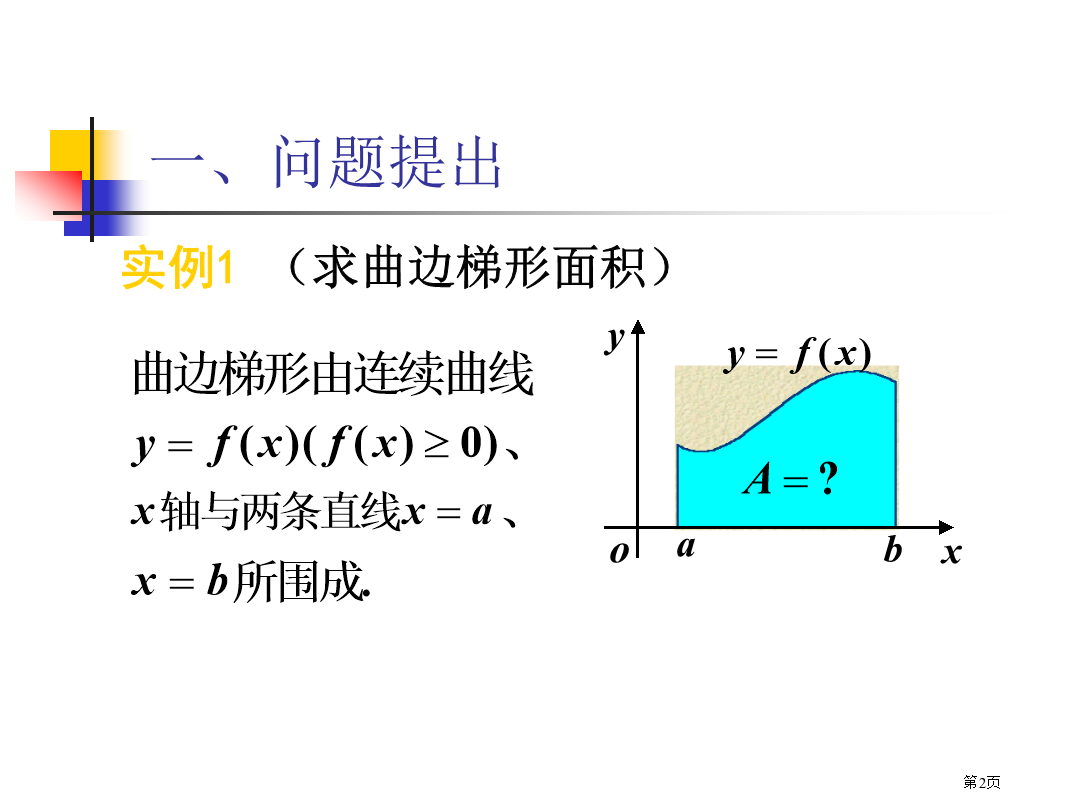
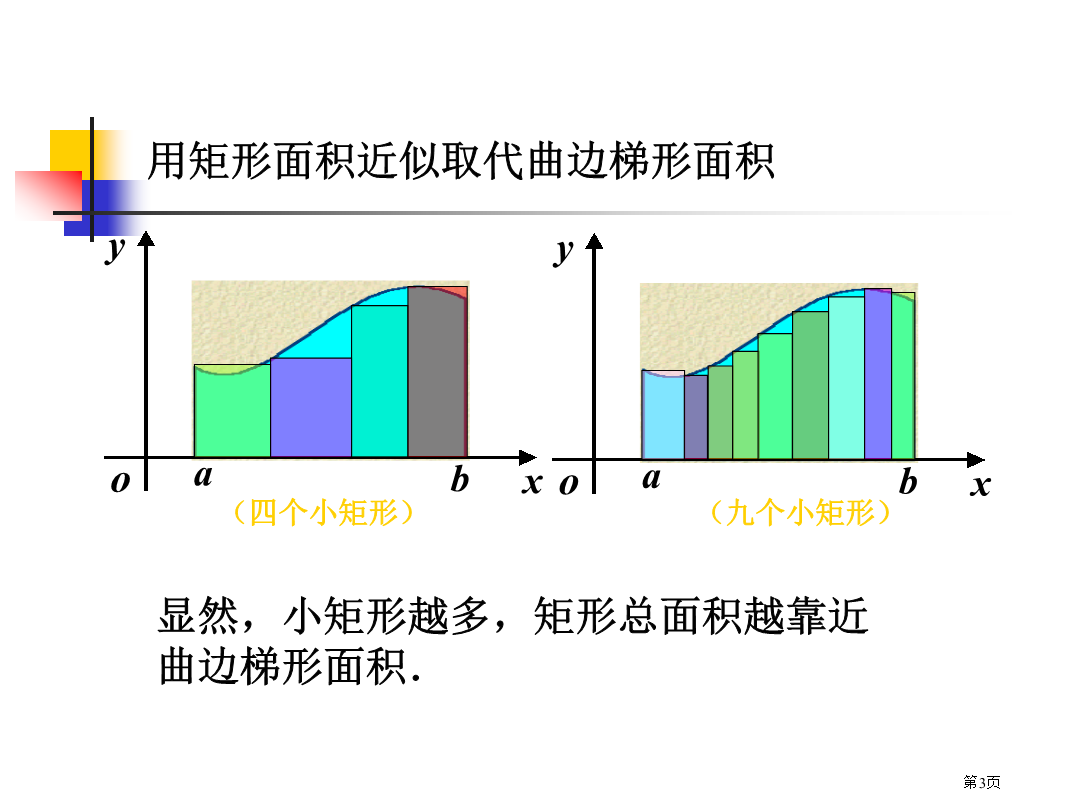
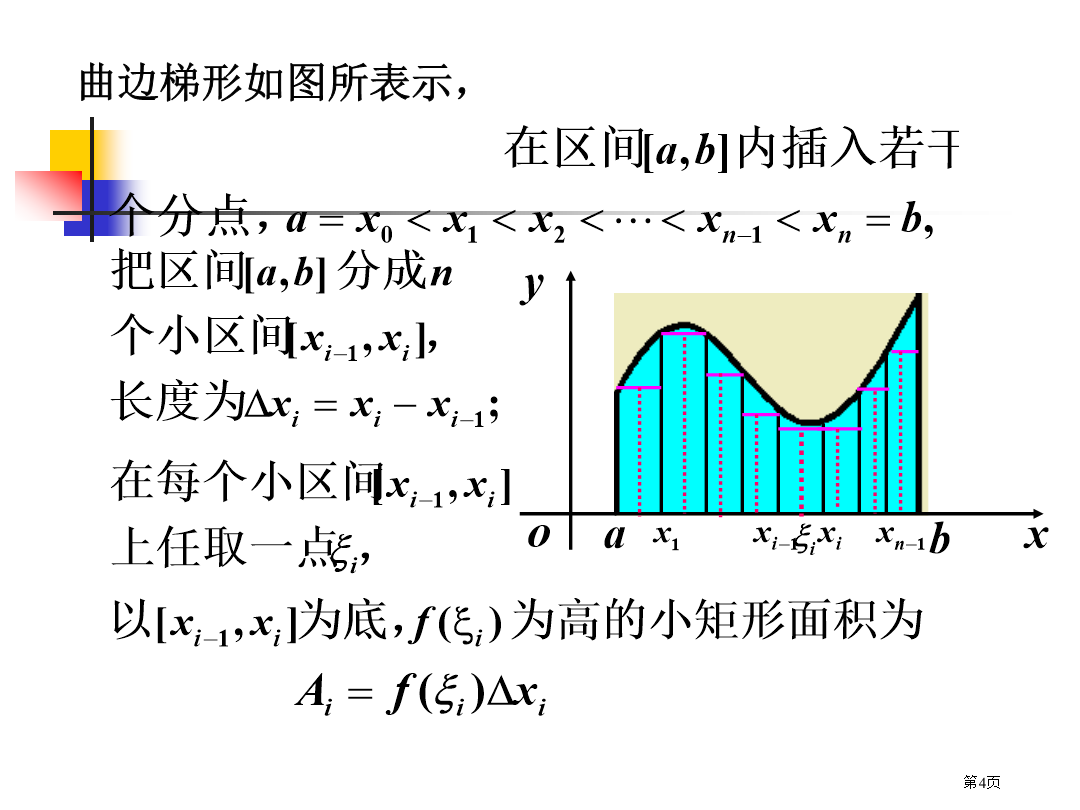
定积分曲边梯形如图所表示，曲边梯形面积近似值为实例2（求变速直线运动旅程）（1）分割二、定积分定义被积函数注意：定理1曲边梯形面积几何意义：例1利用定义计算定积分五、定积分性质证证补充：不论相对位置怎样,上式总成立.证解性质5推论：证证解证使Th5.2(推广积分第一中值定理）考查定积分证由积分中值定理得计算以下导数补充例1求定理2（原函数存在定理）定理3（微积分基本公式）令微积分基本公式表明：例4求例6求则有定理证应用换元公式时应注意:例1计算例2计算例3计算三角代换和根式代换例4计算证总结：1、定积分公

2024-02-10

2.4MB

微积分公式专题培训市公开课一等奖百校联赛特等奖课件.pptx

一、问题提出二、对弧长曲线积分概念被积函数2.存在条件：注意：4.性质三、对弧长曲线积分计算注意:推广:例1例2例4四、几何与物理意义五、小结思索题思索题解答练习题练习题答案

2024-02-10

1.3MB

微积分入门专题培训市公开课一等奖百校联赛特等奖课件.pptx

2024-02-12

2.4MB

数值微积分专题培训市公开课一等奖百校联赛特等奖课件.pptx

第四章数值微积分§1.引言关于积分§1.Newton-Cotes型求积公式误差为：从而对于：我们称此公式为Newton-Cotes型求积公式。针对等距分点处函数值：两边积分得到从而得到Newton-Cotes型求积公式在详细计算时，能够取定n=1，2，3，4。此时，还有专用名称称呼，分别为梯形公式、抛物线公式、Cotes公式等，下面给出详细计算格式。一、梯形公式（n=1）即：于是，得到梯形求积公式及其误差为二、抛物线(辛普森-Simpson)公式（n=2）得到抛物线(simpson)求积公式及误差为三、C

2024-02-13

1.5MB