课件-全国-2019_（安徽专版）2020年中考数学复习 第三单元 函数及其图象 第12课时 二次函数的图象与性质课件.pptx

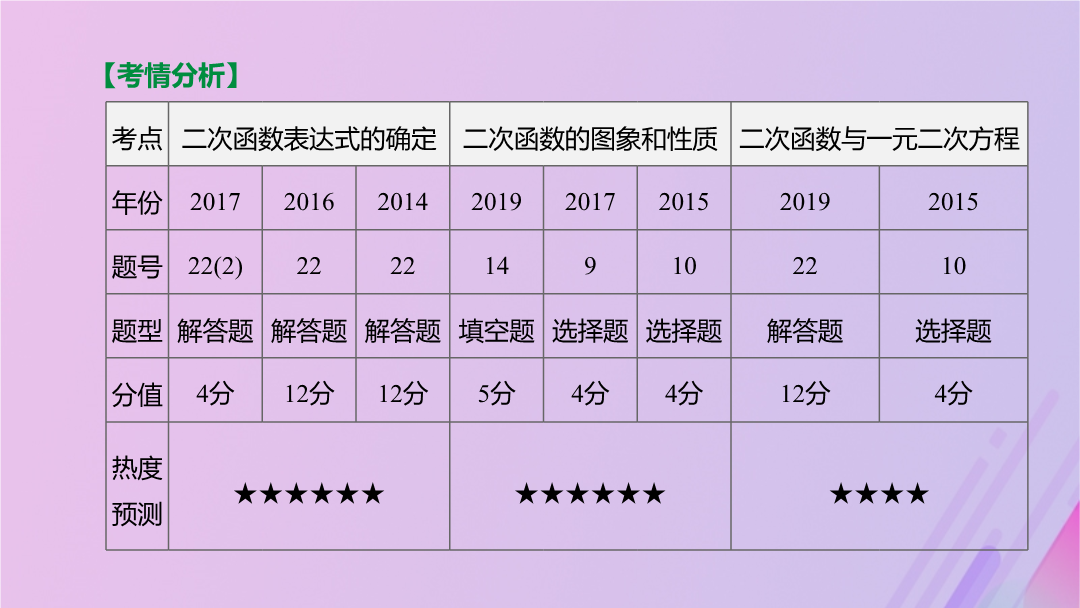
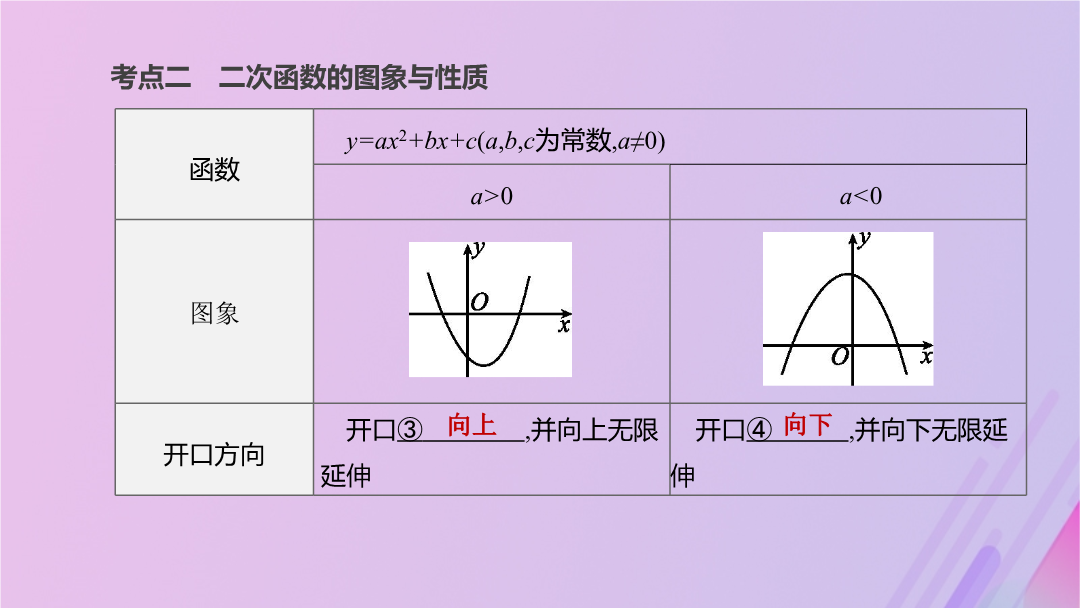
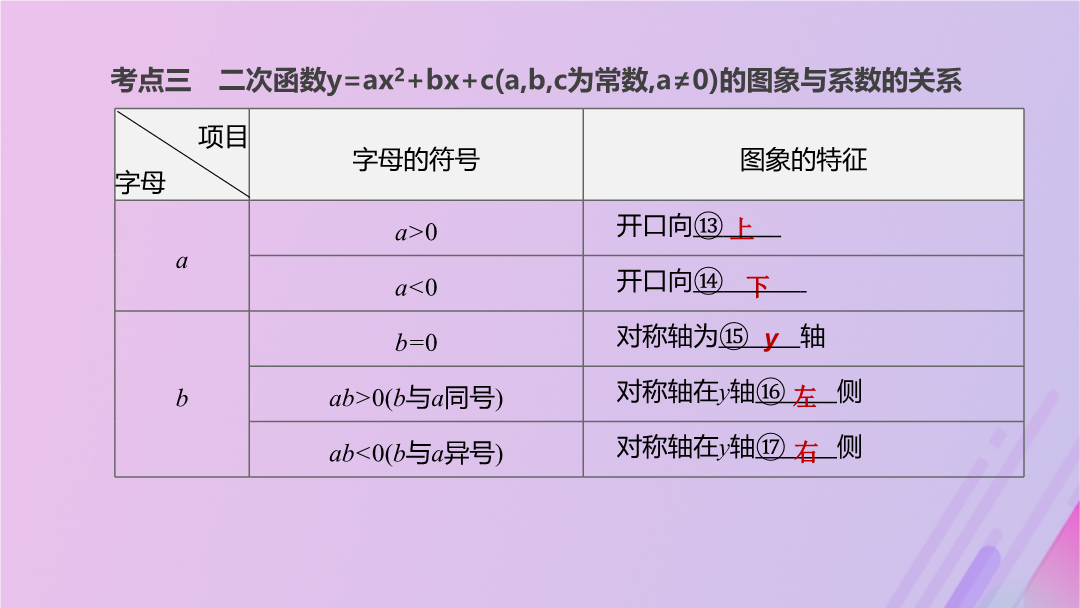
【考情分析】考点一二次函数的概念考点二二次函数的图象与性质(续表)(续表)(续表)考点三二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与系数的关系(续表)(续表)【温馨提示】特别地,对于不等号两边都有字母的,先将右边的字母移到左边,合并同类项化为一般形式后,再用上面的方法判断.考点四二次函数图象的平移考点五二次函数的表示及解析式的求法2.二次函数解析式的确定用待定系数法求二次函数的解析式时,注意解析式的设法,常见情况如下:考点六二次函数与一元二次方程、不等式的关系2.二次函数与不等式的关系(1)ax2+bx+c>0的解集函数y=ax2+bx+c的图象位于x轴上方的部分对应的点的横坐标的取值范围.(2)ax2+bx+c<0的解集函数y=ax2+bx+c的图象位于㉚的部分对应的点的横坐标的取值范围.题组一必会题[答案]D3.已知二次函数y=ax2+bx+c(a≠0)的图象如图12-2所示,则下列结论中正确的是()A.a>0B.c<0C.3是方程ax2+bx+c=0的一个根D.当x<1时,y随x的增大而减小[答案]C[解析]∵二次函数y=ax2-2ax+c的图象经过点(-1,0),∴方程ax2-2ax+c=0一定有一个解为x=-1,∵抛物线y=ax2-2ax+c的对称轴为直线x=1,∴二次函数y=ax2-2ax+c的图象与x轴的另一个交点为(3,0),∴方程ax2-2ax+c=0的解为x1=-1,x2=3.故选C.[答案]9[解析]二次函数y=x2-6x+c的图象与x轴只有一个公共点,说明Δ=b2-4ac=0,即(-6)2-4×1·c=0,所以c=9.[答案]y=2(x+2)2-2[解析]抛物线y=2(x-1)2+2向左平移3个单位,再向下平移4个单位得到y=2(x-1+3)2+2-4=2(x+2)2-2.故得到的抛物线的解析式为y=2(x+2)2-2.题组二易错题[答案]B[解析]二次函数y=-(x-h)2,当x=h时,有最大值0,而当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为-1,故h<2或h>5.当h<2,2≤x≤5时,y随x的增大而减小,故当x=2时,y有最大值,此时-(2-h)2=-1,解得:h1=1,h2=3(舍去),此时h=1;当h>5,2≤x≤5时,y随x的增大而增大,故当x=5时,y有最大值,此时-(5-h)2=-1,解得:h1=6,h2=4(舍去),此时h=6.综上可知,h=1或6,故选B.[答案]m≤4考向一二次函数的图象与性质[答案]C|考向精练|[答案]A解法二:由于一次函数y1=x的图象与二次函数y2=ax2+bx+c的图象有两个不同的交点,且都位于第一象限,所以方程ax2+bx+c=x,即ax2+(b-1)x+c=0有两个不相等的正实数根,所以函数y=ax2+(b-1)x+c的图象与x轴有两个不同的交点,且都在x轴的正半轴上,故选A.2.二次函数y=x2+x+c的图象与x轴有两个交点A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,那么下列判断正确的是()A.当n<0时,m<0B.当n>0时,m>x2C.当n<0时,x1<m<x2D.当n>0时,m<x1[答案]C3.[2019·嘉兴]小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时有如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与x轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2.其中错误结论的序号是()A.①B.②C.③D.④[答案]C考向二二次函数表达式的确定|考向精练|2.已知抛物线y1=-x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(-1,5),点A与y1的顶点B的距离是4.(1)求y1的解析式;(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.2.已知抛物线y1=-x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(-1,5),点A与y1的顶点B的距离是4.(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.考向三二次函数图象特征与a,b,c之间的关系[答案]D【方法点析】解此类问题的一般步骤①根据抛物线的开口方向判定a的符号:开口向上,则a>0;开口向下,则a<0;②根据对称轴的位置和a的符号判定b的符号:对称轴在y轴左侧,则a,b同号;对称轴在y轴右侧,则a,b异号;③由抛物线与y轴的交点判断c的符号:交点在y轴正半轴,则c>0;交点在y轴负半轴,则c<0;④根据a,b,c的符号判定ab,bc