
函数的导数和积分省公开课一等奖全国示范课微课金奖PPT课件.pptx

胜利****实阿






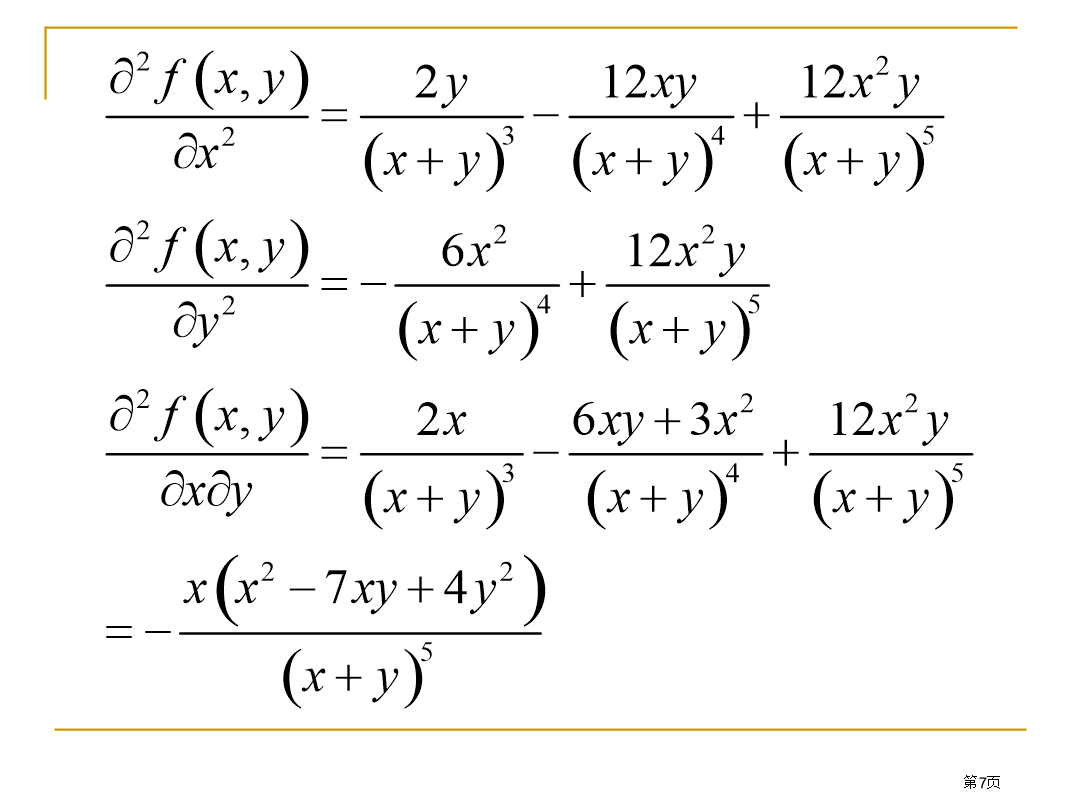



亲,该文档总共42页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

函数的导数和积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
第7章函数导数和积分7.1函数导数M文件运行结果:函数1阶导数:f1=-1/2/cos(x)^(1/2)*sin(x)-sin(x)-x*cos(x)函数2阶导数:f2=-1/4/cos(x)^(3/2)*sin(x)^2-1/2*cos(x)^(1/2)-2*cos(x)+x*sin(x)7.1.2二维函数和参数方程偏导数1、二维函数偏导数使用符号求二维函数fun(x,y)偏导数函数调用格式是:diff(diff(fun,x),y)diff(diff(fun,y),x)其中,fun是函数符号表示式;x和

极限导数和积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
极限、导数和积分符号微积分1.创建符号变量f=sym(‘F’)创建符号表示式F,赋予f;>>g=sym('g(x,y)')g=g(x,y)1.2符号变量算术运算1.2符号变量表示式化简3.因式分解:factor(A):对符号表示式A程序:symsxyfactor(x^3-y^3)结果:ans=(x-y)*(x^2+x*y+y^2)1.2符号变量表示式化简符号变量表示式(化简、提取和代入)符号微积分(化简、提取和代入)2极限limit(‘表示式’,var,a):求当var→a,表示式极限例:求极限:syms
有理函数的积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
第四节有理函数积分一、有理函数积分依据代数学一个主要结论——怎样将真分式分解为部分分式之和?第三步:待定系数确实定:四种经典部分分式积分:例1.将以下真分式分解为部分分式:并将A、B值代入(1)(三、解线性方程组法)(3)例2.求例3.求例4.求例5.求说明:二、可化为有理函数积分举例例6.求2.简单无理函数积分例7.求例8.求内容小结作业

函数与导数省公开课一等奖全国示范课微课金奖PPT课件.pptx
第二模块函数与导数第四讲函数概念基础自测1.(·江西模拟)函数y=f(x)图象与x=4交点个数为()A.一个B.二个C.最少一个D.至多一个解析:因为函数定义域不确定,当定义域中含有4时,依据函数定义,x=4与y=f(x)图象只有一个交点,当函数定义域中不含有4时,x=4与y=f(x)交点个数为零,故答案为D.答案:D5答案:C3.(·广东模拟)已知映射f:A→B,其中A=B=R,对应法则f:x→y=-x2+2x,对于任意实数k∈B,在集合A中存在不一样两个原象,则k取值范围是()A.k>1B.k≤1C.

复变函数的积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
第3章复变函数积分3.1:复变函数积分重点内容:3.1复变函数积分定义3.1.1有向曲线在讨论复变函数积分时,将要用到有向曲线概念,假如一条光滑或逐段光滑曲线要求了其起点和终点,则称该曲线为有向曲线,曲线方向是这么要求:(1)假如曲线是开口弧段,若要求它端点为起点,为终点,则沿曲线从到方向为曲线正方向(简称正向),把正向曲线记为或.而由到方向称为负方向(简称负向),负向曲线记为.(2)假如是简单闭曲线,通常总要求逆时针方向为正方向,顺时针方向为负方向.(3)假如是复平面上某一个复连通域边界曲线,则正方向这
