第十二章动量矩定理.pdf

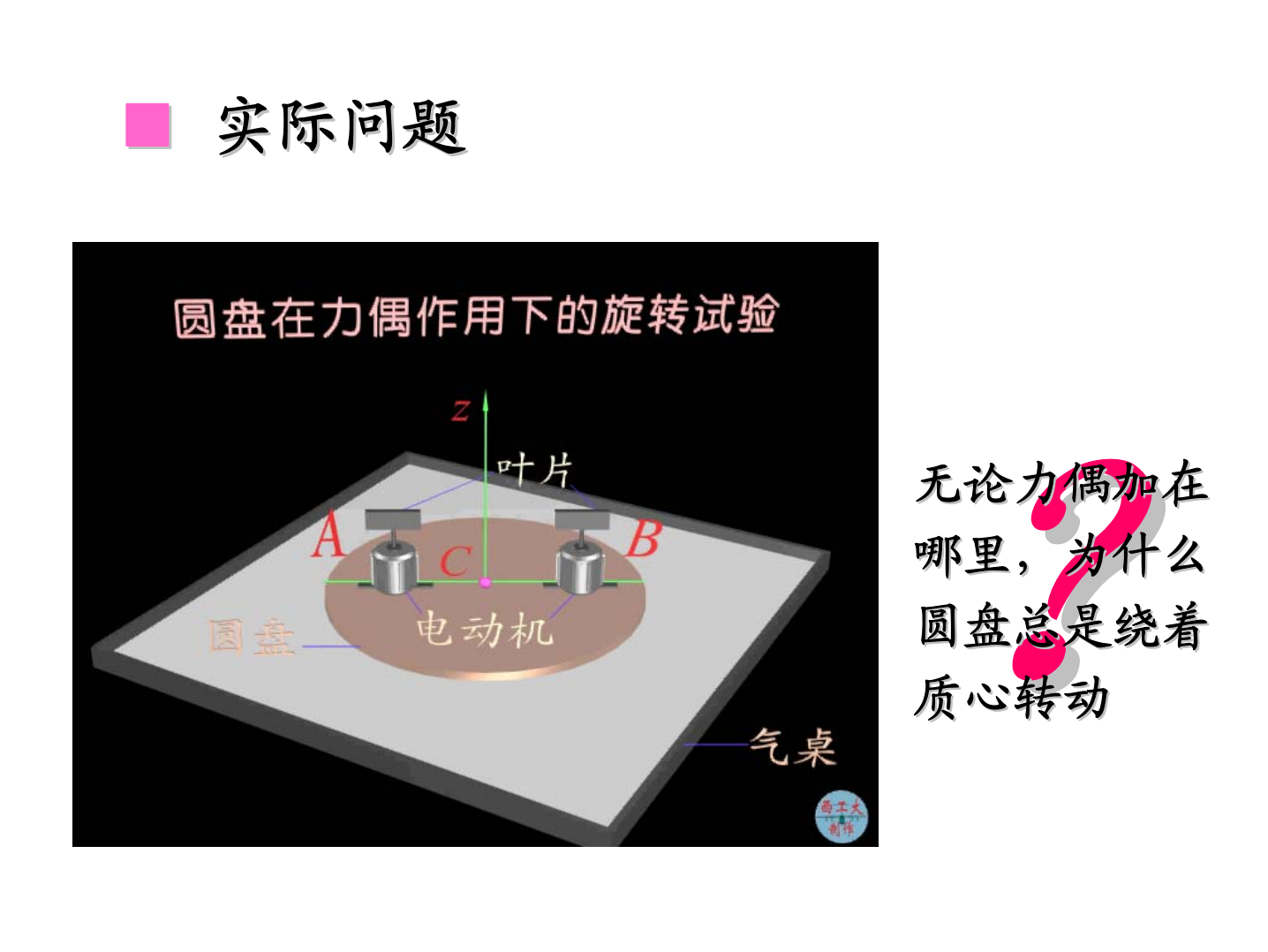
第十二章第十二章动量矩定理动量矩定理第十二章第十二章(Theoremof动量矩定理动量矩定理theMomentofMomentum)20112011年年55月月88日日第十二章动量矩定理§12-1动量矩§12-2动量矩定理§12-3刚体对轴的转动惯量§12-4刚体定轴转动微分方程？？谁最先到达顶点谁最先到达顶点实际问题实际问题■■？？谁最先到达顶点谁最先到达顶点实际问题实际问题■■■■实际问题实际问题无论力偶加在无论力偶加在哪里，为什么哪里，为什么圆盘总是绕着圆盘总是绕着质心转动质心转动■■实际问题实际问题为什么二者转为什么二者转动方向相反动方向相反§12-1动量矩1.1.质点的动量矩质点的动量矩O(mvM)MMOO()()mmmmvrvr=×=×vv动量矩矢量是定位矢量动量矩矢量是定位矢量&质点对质点对zz轴的动量矩轴的动量矩&mvOrMm(vMv)=⎡(m)⎤zO⎣⎦z对比力对点之矩对比力对点之矩MMOO((FrFFrF))==××对比力对轴之矩对比力对轴之矩M(FMF)=⎡()⎤zO⎣⎦zzz2.2.质点系的动量矩质点系的动量矩vviri第第个质点的动量矩个质点的动量矩miiim2m1OyyMMOiiiOiii()()mmmmvrvr=×=×iiiivvm质点系的动量矩质点系的动量矩xxm3nnnLOOiiiii==×∑∑Mv()mmrvii==11质点系对质点系对zz轴的动量矩轴的动量矩nLMmzzi=∑()vii=13.3.质点系为刚体时的动量矩质点系为刚体时的动量矩nn●●刚体平移时刚体平移时Lrvrv=rvOii=∑∑×=mm()iiC×m×ii==11LOC=rv×mC●●刚体定轴转动刚体定轴转动znnLMmmvrzzi==∑∑()viiiiii==11nnmviiωrr2r=⋅=∑∑mmiiiωiiriii==11n2ωω记Jzi=∑mrii为刚体对为刚体对zz轴的轴的转动惯量转动惯量LJzz=ω§12-2刚体对轴的转动惯量（§12-3））★★常见规则形状物体的转动惯量常见规则形状物体的转动惯量●●均质圆盘（圆柱）：质量为均质圆盘（圆柱）：质量为mm,,半径为半径为RRR1J=mR2zzOO2C●●均质细直杆：质量为均质细直杆：质量为mm，杆长为，杆长为llOCC1212J==JmlJoz==JmlCzc123●●均质圆环：质量为均质圆环：质量为mm，半径为，半径为RR2JO=mR★★平行移轴定理平行移轴定理+=mdJJ2zzCCC为质心为质心★★回转半径回转半径2Jmzz=ρ其中ρz—回转半径回转半径★★确定确定转动惯量的方法转动惯量的方法●●积分法积分法●●组合法组合法●●实验法实验法§12-3动量矩定理（§12-2）★★质点的动量矩定理质点的动量矩定理★★质点系的动量矩定理质点系的动量矩定理★★动量矩守恒动量矩守恒★★质点的动量矩定理质点的动量矩定理d(d(mmvv))由由==FFddttd(d(mmvv))d(d(mmmmvrvrvrvr))d(d(××))ddrrFrrF××=×=×rvrv×=×=−×−×mmddttddddddttttttddrrd(d(mmmmvrvvrv))d(d(××))vv==rr×=×=ddttddddttttdLO=MF()dtO矢量式矢量式质点对固定点的动量矩对时间的导数等于作质点对固定点的动量矩对时间的导数等于作用于质点上的力对该点的矩。用于质点上的力对该点的矩。★★质点系的动量矩定理质点系的动量矩定理00ddr×=mvMF()ieie+MF()∑∑∑∑riiiiii×=mvMFOiOi()+∑∑MFOiOi()ddttF1iiiiiiz1vvi=MF()ee=∑∑MFOiOi()FmF2m2iim1OrriiydLOem=Mxm3n∑OFdtFnFi质点系对于定点质点系对于定点OO的动量矩对时间的一阶导的动量矩对时间的一阶导数，等于作用在系统上数，等于作用在系统上所有外力所有外力对于同一对于同一点的主矩点的主矩..●●质点系对于定点的动量矩定理（矢量式）质点系对于定点的动量矩定理（矢量式）ddLLOO==MMeeddtt∑∑OO●●质点系对于定点的动量矩定理（投影式）质点系对于定点的动量矩定理（投影式）dLx=Medt∑xdLy=Medt∑ydLz=Medt∑z例例1212--11已知已知mJ、、、、、Om121mrr2，，不计摩擦。不计摩擦。求：求：（（11）滑轮转动的角加速度；）滑轮转动的角加速度；αα（（22）滑轮）滑轮OO处的约束力；处的约束力；Fωω（（33）绳索的拉力。）绳索的拉力。ON解：解：（（11）取系统为研究对象）取系统为研究对象mgO=Oω++rvmrvmJL222111？？++v222（顺时针）ω(O11++=rmrmJ22)m2gv1(