
单摆实验报告.doc

骊蓉****23





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

单摆实验报告.doc
广州大学学生实验报告院(系)名称物理系班别姓名专业名称物理教育学号实验课程名称普通物理实验I实验项目名称力学实验:单摆实验时间实验地点实验成绩指导老师签名一、实验目的mgcosθmgsinθLθθmg(1)学会用单摆测定当地的重力加速度。(2)研究单摆振动的周期和摆长的关系。(3)观察周期与摆角的关系。二、实验原理如图所示,将一根不易伸长而且质量可忽略的细线上端固定,下端系一体积很小的金属小球绳长远大于小球的直径,将小球自平衡位置拉至一边(摆角小于5°),然后释放,小球即在平衡位置左右往返作周期性的摆动,

单摆实验报告.doc
广州大学学生实验报告院(系)名称物理系班别姓名专业名称物理教育学号实验课程名称普通物理实验I实验项目名称力学实验:单摆实验时间实验地点实验成绩指导老师签名一、实验目的mgcosθmgsinθLθθmg(1)学会用单摆测定当地的重力加速度。(2)研究单摆振动的周期和摆长的关系。(3)观察周期与摆角的关系。二、实验原理如图所示,将一根不易伸长而且质量可忽略的细线上端固定,下端系一体积很小的金属小球绳长远大于小球的直径,将小球自平衡位置拉至一边(摆角小于5°),然后释放,小球即在平衡位置左右往返作周期性的摆动,

单摆实验报告.pdf
广州大学学生实验报告院〔系〕名称物理系班姓名专业名称物理教育别学号实验课程名称普通物理实验I实验工程名称力学实验:单摆实验时间实验地点实验成绩指导老师签名一、实验目的〔1〕学会用单摆测定当地的重力加速度。〔2〕研究单摆振动的周期和摆长的关系。〔3〕观察周期与摆角的关系。θL二、实验原理如下图,将一根不易伸长而且质量可忽略的细线上端固定,下端系一体积很小的金属小球绳长远大于小球的直径,将小球mgsinθ自平衡位置拉至一边〔摆角小于5°〕,然后释放,小球即在平θ衡位置左右往返作周期性的摆动,这里的装置就是单摆
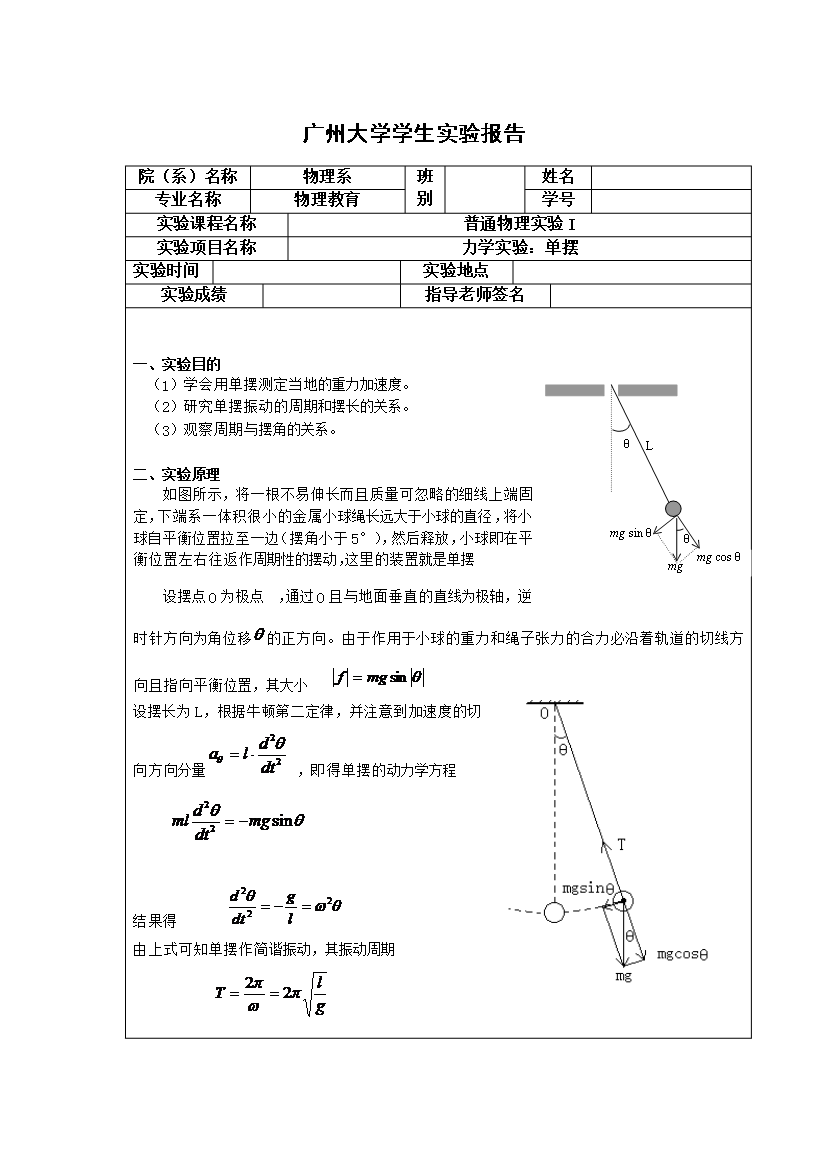
单摆实验报告.doc
广州大学学生实验报告院(系)名称物理系班别姓名专业名称物理教育学号实验课程名称普通物理实验I实验项目名称力学实验:单摆实验时间实验地点实验成绩指导老师签名一、实验目的mgcosθmgsinθLθθmg(1)学会用单摆测定当地的重力加速度。(2)研究单摆振动的周期和摆长的关系。(3)观察周期与摆角的关系。二、实验原理如图所示,将一根不易伸长而且质量可忽略的细线上端固定,下端系一体积很小的金属小球绳长远大于小球的直径,将小球自平衡位置拉至一边(摆角小于5°),然后释放,小球即在平衡位置左右往返作周期性的摆动,

单摆与长度测量实验报告.pdf
广东第二师范学院实验报告指导老师:傅晓东2013/10/11生物系12科学教育曾娜12550803026实验一长度测量一、实验目的:学习螺旋测微计、游标卡尺的的结构、工作原理和真确的使用方法,为后续实验的顺利进行做好充分准备。通过本实验还要初步掌握实验数据记录、有效数字运算和误差计算规则以及测量结果的表示方法。二、实验仪器:米尺、游标卡尺(规格:0-125mm)、螺旋测微计(规格:0.02mm0-150mm)三、实验原理:1)米尺:米尺的分度值为1mm,,用它测量物体的长度时,只能准确读到毫米这一位,毫米
