
平面杆件体系的几何组成分析.ppt

胜利****实阿









亲,该文档总共17页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

平面杆件体系的几何组成分析.doc
第四章平面杆件体系的几何组成分析4.1几何组成分析的基本概念结构是由若干根杆件通过结点间的连接及与支座连接组成的。结构是用来承受荷载的,因此必须保证结构的几何构造是不可变的。例如:4.1.1几何不变体系和几何可变体系1.几何不变体系(geometricallyunchangeablesystem):在不考虑材料应变的条件下,体系的位置和形状不能改变。2.几何可变体系(geometricallychangeablesystem):不考虑材料的变形,在微小荷载作用下,不能保持原有几何形状和位置的体系。图4-1

平面杆件体系的几何组成分析.ppt
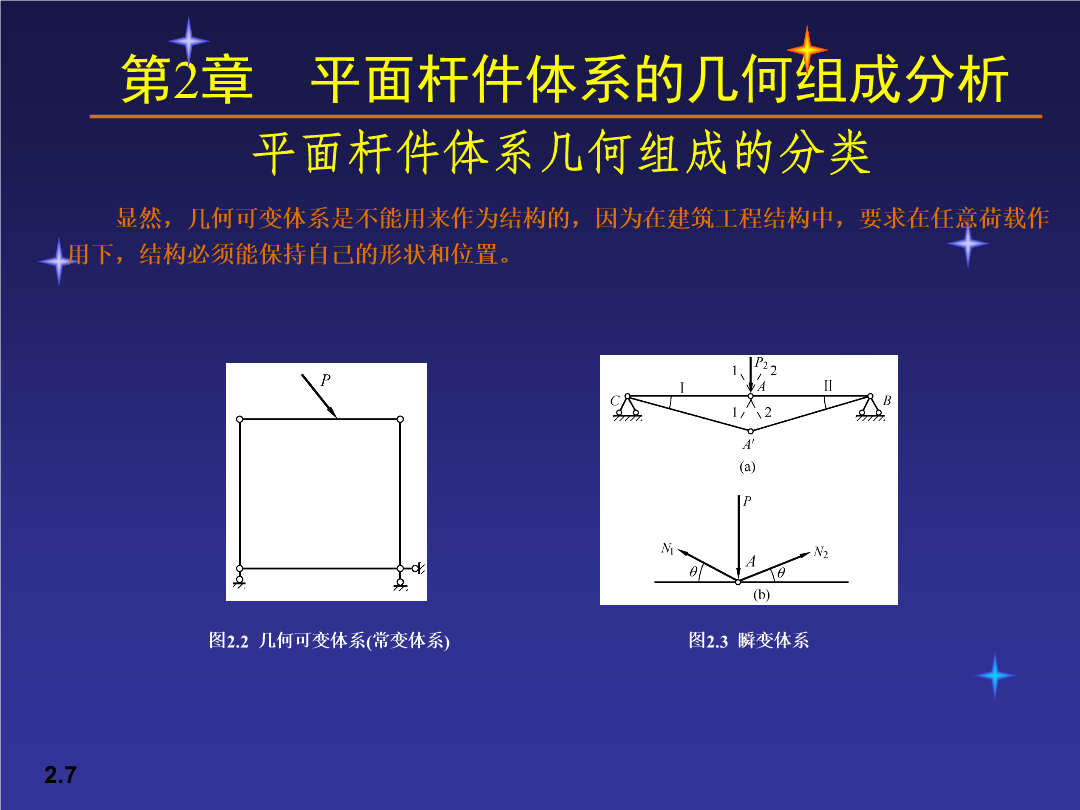
第2章平面杆件体系的几何组成分析平面杆件体系几何组成的分类无多余约束的平面几何不变体系简单组成规则平面杆系几何组成分析举例习题教学要求:本章要求学生了解平面杆系的分类,掌握平面几何不变体系的组成规则、构造特点,理解工程中所用结构必须为几何不变体系。能利用几何不变体系的组成规则对简单平面杆系进行几何组成分析。建筑力学研究的重点是平面杆系结构。所谓平面杆系是由若干杆件按照一定方式互相连接而组成的。对平面体系的几何组成进行分析,称为几何组成分析。其目的在于:(1)判断某一体系是否几何可变,以决定它能否作为结构使

平面杆件体系的几何组成分析.ppt
第2章平面杆件体系的几何组成分析平面杆件体系几何组成的分类无多余约束的平面几何不变体系简单组成规则平面杆系几何组成分析举例习题教学要求:本章要求学生了解平面杆系的分类,掌握平面几何不变体系的组成规则、构造特点,理解工程中所用结构必须为几何不变体系。能利用几何不变体系的组成规则对简单平面杆系进行几何组成分析。建筑力学研究的重点是平面杆系结构。所谓平面杆系是由若干杆件按照一定方式互相连接而组成的。对平面体系的几何组成进行分析,称为几何组成分析。其目的在于:(1)判断某一体系是否几何可变,以决定它能否作为结构使

02平面杆件结构的几何组成分析.docx
第二章平面杆件结构的几何组成分析???本章问题:什么是几何不变体系和几何可变体系?什么是自由度?什么是刚片?什么是多余约束?什么是瞬变体系?瞬铰?什么是三刚片规则?两刚片规则?二元体规则?什么是静定结构?超静定结构?前言:静定结构:其几何特征是无多余约束的几何不变体系。(1)若静定结构撤销约束或不适当的更改约束配置可以使其变成可变体系,(2)增加约束又可以使其成为有多余约束的不变体系(即超静定结构)。因此,熟练掌握静定结构的组成规则,不仅可以正确地确定超静定结构中的多余约束数,而且可以正确地通过减少约束使

结构力学杆件体系的几何组成分析教案.pptx
会计学1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析1.几何组成分析方法1:若基础与其它部分三杆相连,去掉基础只分析其它部分方法1:若基础与其它部分三杆相连,去掉基础只分析其它部分方法1:若基础与其它部分三杆相连,去掉基础只分析其它部分方法1:若基础与其它部分三杆相连,去掉基础只分析其它部分方法1:若基础与其它部分三杆相连,去掉基础只分析其它部分方法1:若基础与
