测量不确定度培训演稿PPT课件.ppt

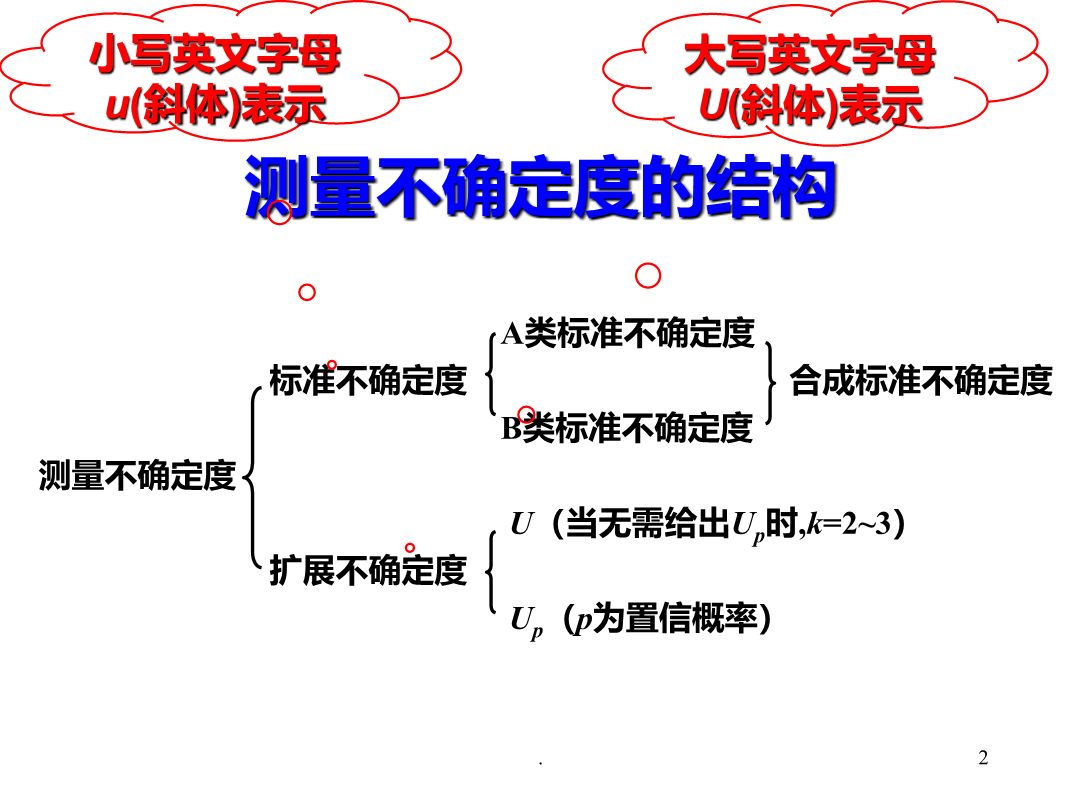
测量不确定度评定测量不确定度的结构3一)正确表示不确定度的意义二)、不确定度的主要应用领域三)、不确定度评定应用的具体场合1数理统计基本知识2.最佳估值┈┈多次测量的平均值3.分散范围（区间）－标准偏差4分布┈┈数据散布的“形状”概率p=95.45%5测量基本术语测量误差的定义关于允差准确度测量不确定度标准不确定度和扩展不确定度不确定度A类和B类评定方法标准不确定度合成标准不确定度扩展不确定度包含因子k实验标准(偏)差计算式—贝塞尔公式自由度如何理解测量不确定度？U=1u=1.0%表1.1测量误差与测量不确定度的主要区别表1.1测量误差与测量不确定度的主要区别表1.1测量误差与测量不确定度的主要区别表1.1测量误差与测量不确定度的主要区别6产生测量不确定度的原因和测量模型化建立数学模型(续)7建立数学模型(续)第二节标准不确定度A类评定实验标准(偏)差计算式—贝塞尔公式平均值的标准（偏）差观测次数n充分多，才能使A类不确定度评定可靠，一般认为n应大于5。但也要视实际情况而定，当A类不确定度分量对合成标准不确定度的贡献较大时，n不宜太小，反之，当A类不确定度分量对合成标准不确定度的贡献较小时n小一些关系也不大。由实验标准偏差的分析可知，单次测量的实验标准偏差s(xi)是一个特定的被测量和测量方法的固有特性，该特性表征了各单个测得值的分散性。此处所说的测量方法包括测量原理、测量设备、测量条件、测量程序以及数据处理程序等。在重复性条件下或复现性条件下进行规范化常规测量，通常不需要每次测量都进行A类标准不确定度评定，可以直接引用预先评定的结果。所谓规范化常规测量，是指明确规定了方法、程序、条件的测量，如已通过实验室认可的检测或校准项目的测量。如果事先对某被测量X进行n次独立重复测量，其实验标准差为s(xi)。若随后的规范化常规测量只是由一次测量就直接给出测量结果，则该测量结果的标准不确定度u(x)就等于事先评定的实验标准差s(xi)，即u(x)s(xi)。如果随后的测量进行了几次测量(典型情况是n′＝3)，而且将n′次测量的平均值作为结果提供给客户，则算术平均值的实验标准差应等于实验标准差s(xi)除以次数n′的平方根，相应的标准不确定度为【实例】某实验室事先对某一电流量进行n＝10次重复测量，测量值列于表5.1。由贝塞尔公式计算得到单次测量的估计标准偏差s(x)＝0.074mA。①在同一系统中在以后做单次（n′＝1）测量，测量值x＝46.3mA，求这次测量的标准不确定度u(x)。②在同一系统中在以后做3次（n′＝3）测量，求这3次测量结果的标准不确定度。表2.1对某一电流量进行n＝10次重复测量的测量值【解】①对于单次测量，则其标准不确定度等于1倍单次测量的标准偏差：x＝46.3mA，u(x)=s(x)=0.074mA。【解】②对于n′＝3次测量，测量结果为：的标准不确定度为：不确定度A类评定的独立性不确定度A类评定的独立性其他几种常用的标准不确定度A类评定方法：★合并样本标准差★极差★最小二乘法★阿伦方差合并实验标准差JJF1059介绍了计算合并实验标准差的方法。对某量进行组测量，有两种情况：若每组独立观测次数相同，均为n，进行组观测的合并实验标准差按下式计算：式中Si2为每组观测的方差。b)若每组独立观测次数不同，分别为ni;自由度分别为：vi=ni-1m组观测的合并实验标准差按下式计算：合并实验标准差sp的自由度为：计算多组观测的合并实验标准差的前题是各组测量应比较接近。第三节标准不确定度B类评定（由于系统效应导致的不确定度）1.以前的观测数据；2.对有关技术资料的测量仪器特性的了解和经验；3.生产企业提供的技术说明文件；4.校准证书（检定证书）或其他文件提供的数据、准确度的等级或级别，包括目前仍在使用的极限误差、最大允许误差等；5.手册或某些资料给出的参考数据及其不确定度；6.规定试验方法的国家标准或类似技术文件中给出的重复性限或复现性。B类不确定度的评定方法(2)已知扩展不确定度U和包含因子k如果估计值xi来源于制造部门的说明书、校准证书、手册或其他资料，其中同时还明确给出了其扩展不确定度U(xi)是标准不确定度u(xi)的k倍，指明了包含因子k的大小，则标准不确定度u(xi)可取而估计值的方差为其平方。【例】校准证书上指出标称值为1kg的砝码的实际质量m＝1000.00032g，并说明按包含因子k=3给出的扩展不确定度U=0.24mg。则该砝码的标准不确定度为u(m)=0.24mg/3=80g，估计方差为。相应的相对标准不确定度urel(m)为【特别提示】在这个例子中，砝码使用其实际值1000.00032g，而不使用其标称值，即砝码是以“等”使用。评定的标准不确定度80g是1000.00032g标准不确定度。(