ARCH模型和GARCH模型0.doc

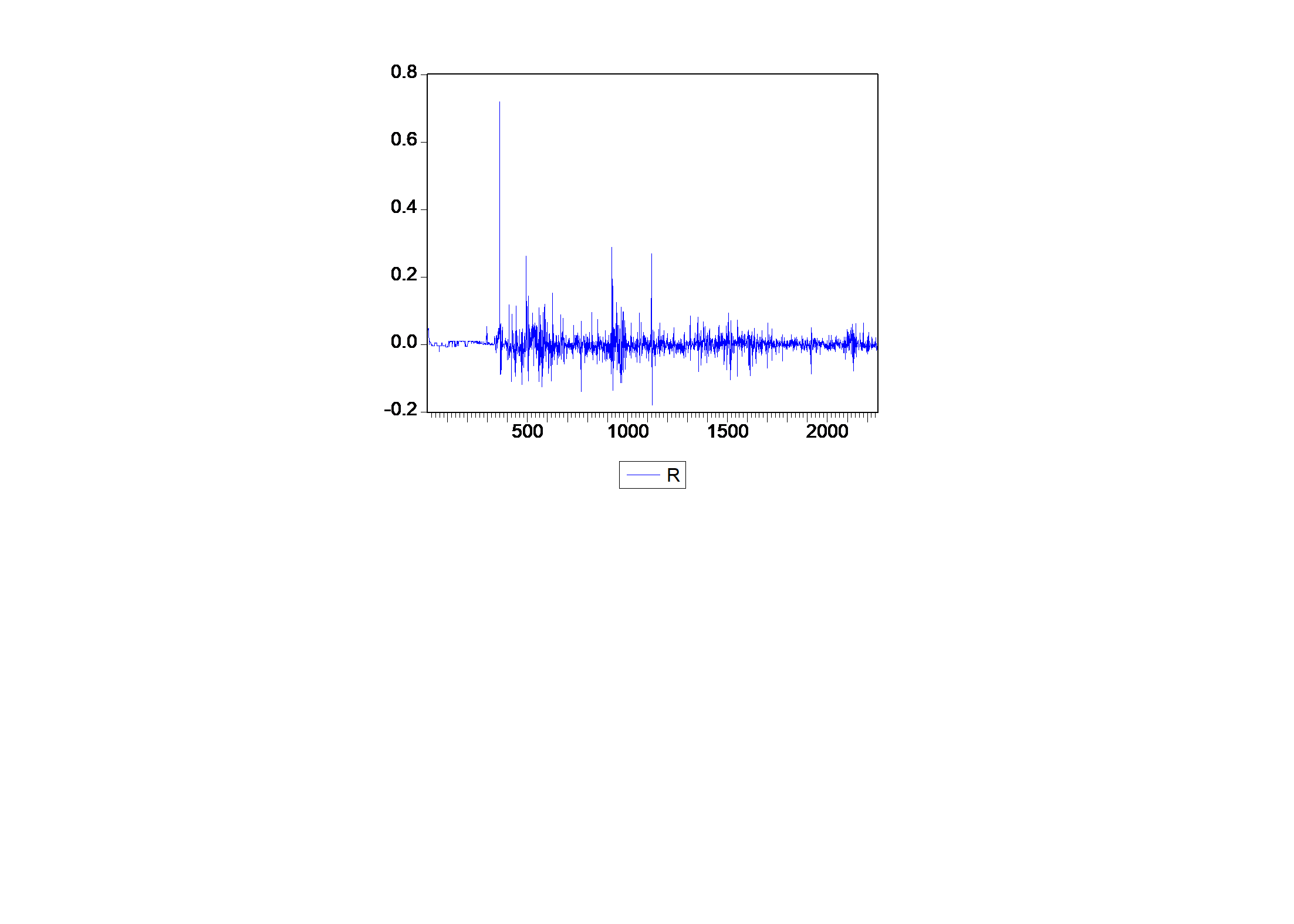
第7章、ARCH模型和GARCH模型研究内容：研究随时间而变化的风险。（回忆：Markowitz均值－方差投资组合选择模型怎样度量资产的风险）本章模型与以前所学的异方差的不同之处：随机扰动项的无条件方差虽然是常数，但是条件方差是按规律变动的量。波动率的聚类性（volatilityclustering）：一段时间内，随机扰动项的波动的幅度较大，而另外一定时间内，波动的幅度较小。如图，§1、ARCH模型1、条件方差多元线性回归模型：条件方差或者波动率（Conditionvariance，volatility）定义为其中是信息集。2、ARCH模型的定义Engle（1982）提出ARCH模型（autoregressiveconditionalheteroskedasticity，自回归条件异方差）。ARCH(q)模型：（1）的无条件方差是常数，但是其条件分布为（2）其中是信息集。方程（1）是均值方程（meanequation）：条件方差，含义是基于过去信息的一期预测方差方程（2）是条件方差方程（conditionalvarianceequation），由二项组成常数ARCH项：滞后的残差平方习题：方程（2）给出了的条件方差，请计算的无条件方差。证明：利用方差分解公式：Var(X)=VarY[E(X|Y)]+EY[Var(X|Y)]由于，所以条件均值为0，条件方差为。那么，推出，说明3、ARCH模型的平稳性条件在ARCH(1)模型中，观察参数的含义：当时，当时，退化为传统情形，ARCH模型的平稳性条件：（这样才得到有限的方差）4、ARCH效应检验ARCHLMTest：拉格朗日乘数检验建立辅助回归方程此处是回归残差。原假设：H0：序列不存在ARCH效应即H0：可以证明：若H0为真，则此处，m为辅助回归方程的样本个数。R2为辅助回归方程的确定系数。Eviews操作：①先实施多元线性回归②view/residual/Tests/ARCHLMTest§2、GARCH模型的实证分析从收盘价，得到收益率数据序列。seriesr=log(p)-log(p(-1))点击序列p，然后view/linegraph1、检验是否有ARCH现象。首先回归。取2000到2254的样本。输入lsrc，得到DependentVariable:RMethod:LeastSquaresDate:10/21/04Time:21:26Sample:20002254Includedobservations:255VariableCoefficientStd.Errort-StatisticProb.C0.0004320.0010870.3971300.6916R-squared0.000000Meandependentvar0.000432AdjustedR-squared0.000000S.D.dependentvar0.017364S.E.ofregression0.017364Akaikeinfocriterion-5.264978Sumsquaredresid0.076579Schwarzcriterion-5.251091Loglikelihood672.2847Durbin-Watsonstat2.049819问题：这样进行回归的含义是什么？其次，view/residualtests/ARCHLMtest，得到ARCHTest:F-statistic5.220573Probability0.000001Obs*R-squared44.68954Probability0.000002TestEquation:DependentVariable:RESID^2Method:LeastSquaresDate:10/21/04Time:21:27Sample(adjusted):20102254Includedobservations:245afteradjustingendpointsVariableCoefficientStd.Errort-StatisticProb.C0.0001105.34E-052.0601380.0405RESID^2(-1)0.1415490.0652372.1697760.0310RESID^2(-2)0.0550130.0658230.8357660.4041RESID^2(-3)0.3377880.0655685.1516970.0000RESID^2(-4)0.0261430.0691800.3778930.7059RESID^2(-5)-0.0411040.069052-0.5952600.5522RESID^2(-6)-0.0693880.069053-1.0048540.3160RESID^2(-7)0.0056170.0691