
光学相位共轭技术.pptx

胜利****实阿






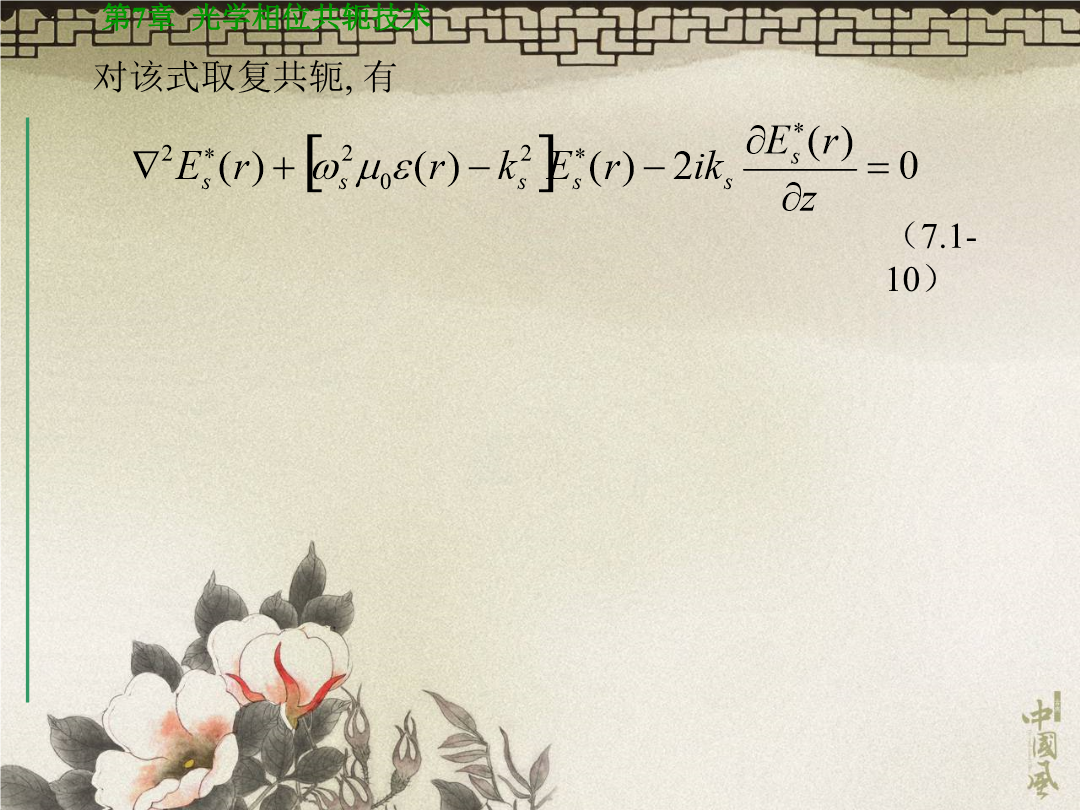

亲,该文档总共104页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

光学相位共轭技术.pptx
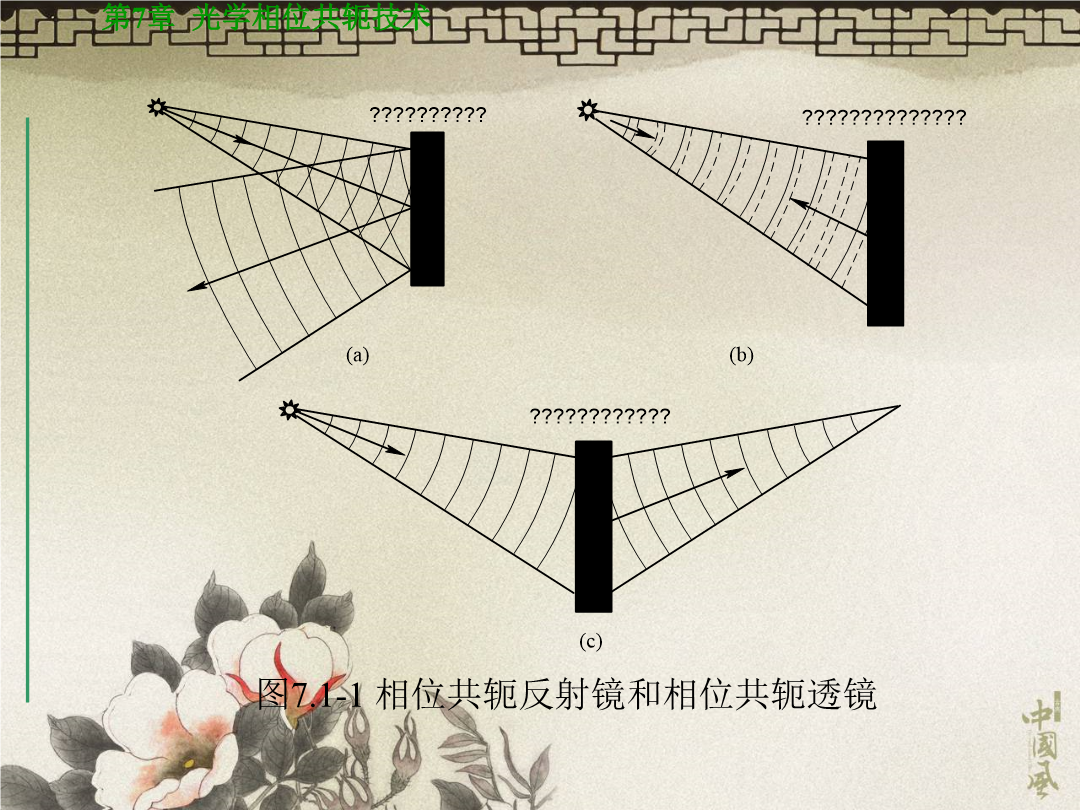
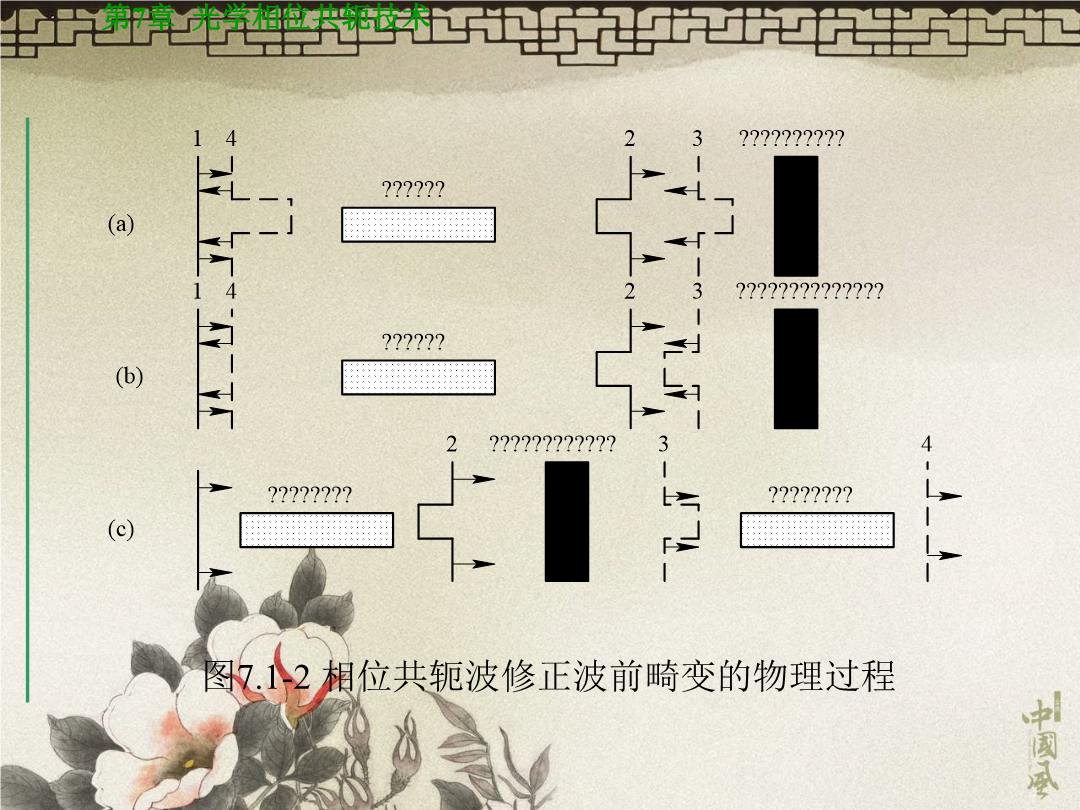
第7章光学相位共轭技术7.1相位共轭波及其物理意义一频率为ωs的单色光波沿z轴方向传播,其光电场表示式为(7.1-1)在有些非线性光学过程如SBS、SRS中,在一定条件下背向散射光场的复振幅也是入射光场复振幅的复共轭,但是它们的频率不同。尽管如此,我们仍将其看作为入射光的背向相位共轭光。在这种情况下,背向相位共轭光电场的表示式为则其相位共轭光电场的复振幅为7.1.2相位共轭波修正波前畸变的物理过程若(7.1-1)式所描述的光波为线偏振光,它在介电常数为ε(r)的非均匀介质中传播时满足标量形式的波动方程:对

光学相位共轭波前畸变校正技术研究的开题报告.docx
光学相位共轭波前畸变校正技术研究的开题报告摘要:相位畸变是指由于光线经过存在着空间非均匀、光路不同程等因素所形成的光的相位变化所引起的影响。其中,波前相位畸变就是一种常见的光学畸变现象,它会严重影响成像质量与光学测量水平。因此,本文旨在研究光学相位共轭波前畸变校正技术,来提高成像质量与测量精度。关键词:相位畸变,波前畸变,共轭波前,校正技术一、引言随着科学技术的发展,越来越多的领域需要通过光学成像、测量来获取精确的数据,比如精确测量地球表面的高度、形态、海洋中的物理量或是医学影像获取等。而光学成像、测量在

基于数字光学相位共轭的新型光镊技术研究.docx
基于数字光学相位共轭的新型光镊技术研究前言光学科技的日新月异,能够利用光进行微观操纵的光镊技术也逐渐成为研究热点。然而,传统的光镊技术存在着诸多限制,如光强、能够捕捉的颗粒大小和类型等限制,因此需要不断研究新的光镊技术来解决这些问题。本文将着重介绍基于数字光学相位共轭的新型光镊技术,包括其原理、实现方法,以及应用领域,并展望其未来的发展趋势。一、数字光学相位共轭技术的原理数字光学相位共轭技术是一种利用数字计算和相位调制的方式来对光进行精确调控的技术。该技术具有诸多优势,如可以实现精确的光束形状、无需传统的

用相位共轭技术补偿湍流畸变.docx
用相位共轭技术补偿湍流畸变相位共轭技术在光学领域中应用广泛,其中之一就是用于补偿湍流畸变。湍流畸变是由大气中的湍流引起的,会引起光束的畸变和传输质量的降低。相位共轭技术可以根据湍流引起的相位畸变,实时修复和补偿光束的传输前后相位差异,从而实现高质量的光束传输。本文将介绍相位共轭技术的原理、方法和应用,并讨论其在湍流畸变补偿中的优势和局限性。1.相位共轭技术原理相位共轭技术基于相位共轭原理,其核心思想是通过获取传输前的光波相位信息,并将其与传输后的光波相位进行比较和修正。具体而言,相位共轭技术分为两个步骤:

基于数字光学相位共轭的新型光镊技术研究的任务书.docx
基于数字光学相位共轭的新型光镊技术研究的任务书任务书一、研究背景光镊是一种利用光学原理实现对微纳米尺度物质的操控技术。它因操作简单、无损、灵活性高等优势受到广泛的关注,并在多个领域得到了广泛的应用。现有的光镊技术主要是基于焦平面光学镊子和光学微成型技术,但由于其受到空气和膜相互作用的影响,限制了操作的精度和效果。数字光学相位共轭(DigitalOpticalPhaseConjugation,DOPC)技术是一种光学复原技术,它可以将一个经过散射介质的光场复原到介质的反面。可以用该技术去除散射和吸收介质对光
