MATLAB在电路中的应用ppt课件.ppt

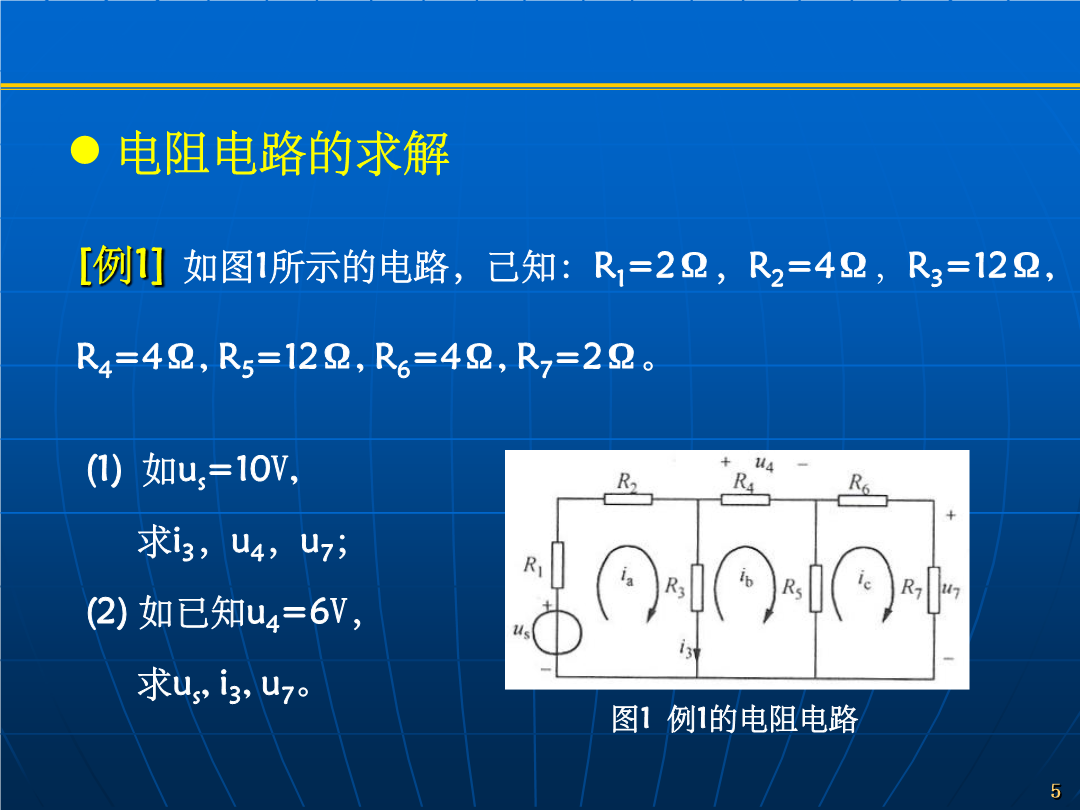
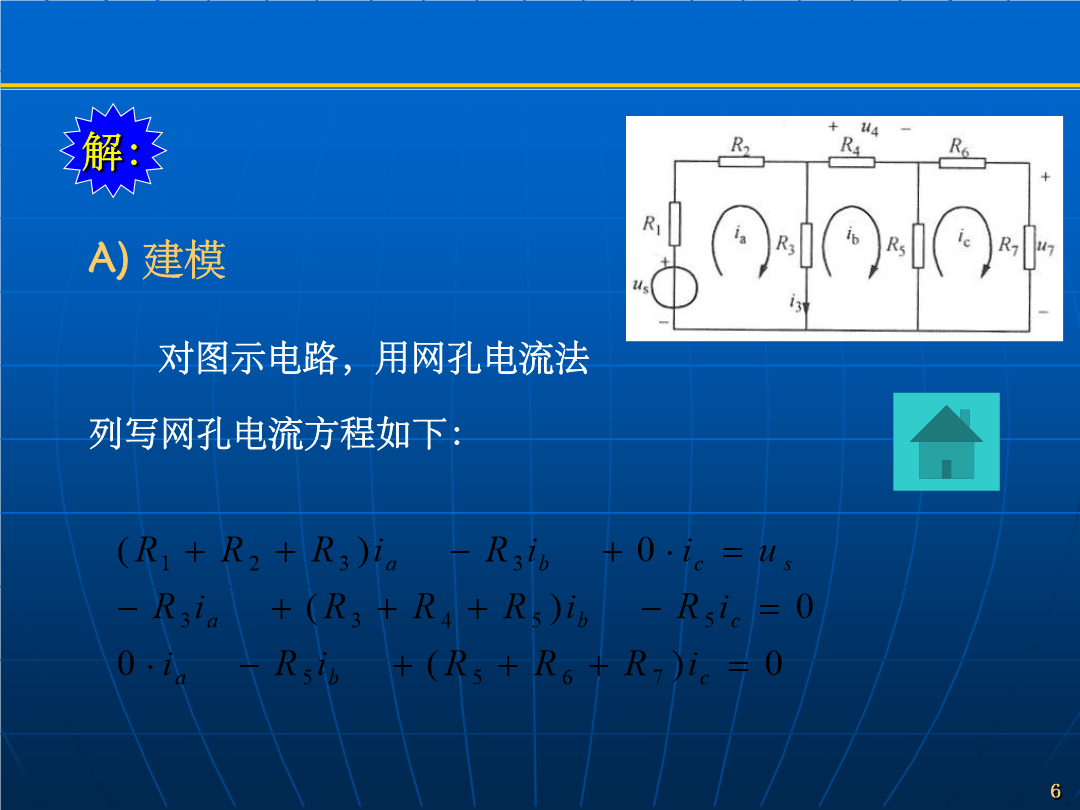
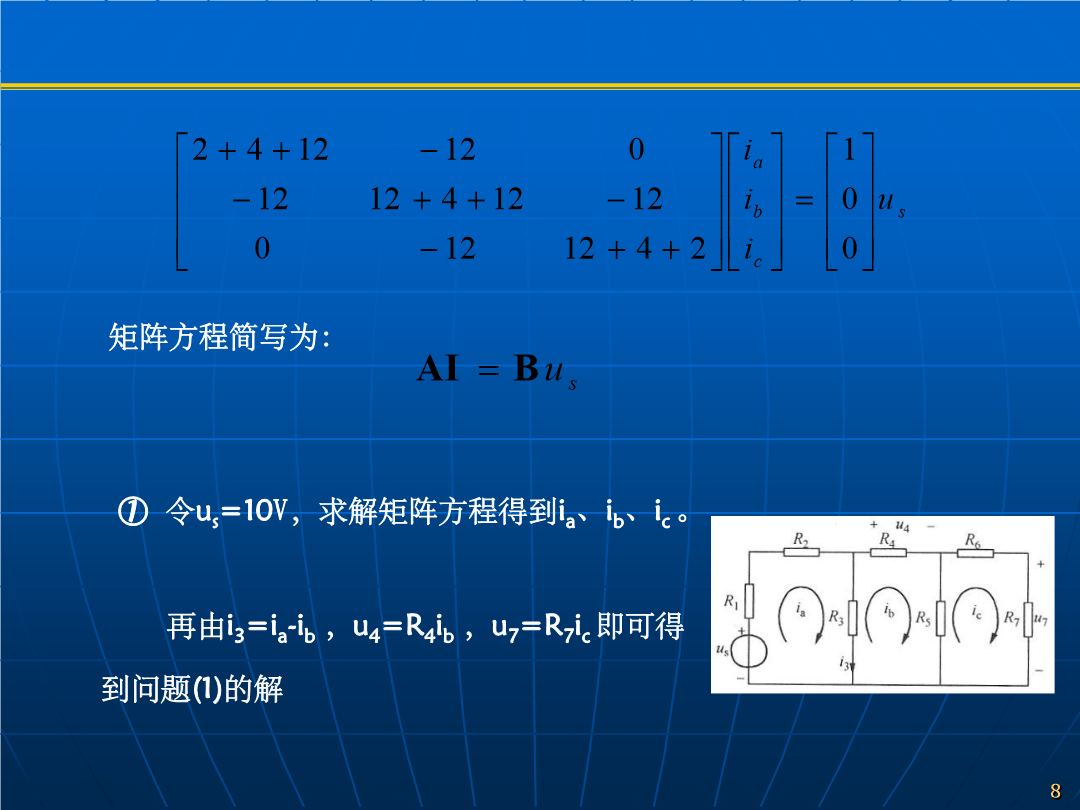
MATLAB应用（三）——Matlab在电路中的应用MATLAB中的变量与常量都是矩阵(标量可看做1×1阶的矩阵，向量可看做n×1或1×n阶的矩阵)，其元素可以是复数和任意形式的表达式，它具有元素群运算能力。学习目的：通过介绍计算电路问题的编程方法和技巧，逐步熟悉MATLAB语言的使用。例题的解法本身，不一定最佳。内容:电阻电路的求解对图示电路，用网孔电流法列写网孔电流方程如下：写成矩阵形式为：矩阵方程简写为：根据电路的线性性质，可令i3=k1us，u4=k2us,u7=k3us,由问题(1)的解求得比例系数，进一步使问题(2)得到解答。程序运行结果补充说明：[例2]对如图2所示的电路，已知R1=R2=R3=4Ω,R4=2Ω,控制常数K1=0.5,k2=4,is=2A,求i1和i2。对图示电路，用节点电压法列写方程得：根据图示电路，控制变量i1、i2与节点电压ua、ub的关系为：Ex02.m[例3]对如图3所示的电路，已知R1=4Ω,R2=2Ω,R3=4Ω，R4=8Ω；is1=2A，is2=0.5A。解：前面的方程写成矩阵形式为：方法Ⅰ：可设ia为一个序列(如ia=0.1，0.2，…，2)，计算相应的ua序列，再用线性拟合，得出如下的直线方程：程序运行结果程序运行结果动态电路的求解对该一阶动态电路可用通用的解决方案[式(2.33)](也称三要素法)求解。根据换路定则(电容电压不变)，得电容初始电压uc(O+)=uc(O-)=-12V。其次求稳定值。经10秒后，开关又闭合到“1”，将t=10代入前面的电压表达式可得电容电压的初始值为：利用通用公式，得到uc(t)、iR2(t)为：程序运行结果[例5]如图5所示的一阶电路,已知R=2Ω，C=0.5F,电容初始电压uc(O+)=4V,激励的正弦电压us(t)=umcosωt,其中um=10V，ω=22rad/s。电路中电容电压的微分方程为：最后得电容电压的全响应为：程序运行结果[例6]考察二阶过阻尼电路的固有响应(零输入响应),图6为典型的二阶动态电路，其固有响应有过阻尼、临界阻尼和欠阻尼三种情况。此例讨论过阻尼情况。按图不难列出关于uc的微分方程为：即α>ω0，表现为过阻尼，其解为：对微分方程作拉氏变换，考虑到初始条件，可得：其中num和den分别为分子、分母多项式系数组成的数组。进而写出：程序运行结果[例7]考察二阶欠阻尼电路的固有响应(零输入响应)，电路同例6。如L=0.5H，C=0.02F。初始值uc(O)=lv,iL=0,试研究R分别为1Ω,2Ω,3Ω,…,1OΩ时,uc(t)和iL(t)的固有响应,并画出波形图。电路的微分方程同例6,为：在此ω0=10，当R=1Ω,2Ω,3Ω,…,1OΩ时，α=1,2,3,…10，显然α=ω0=10为临界阻尼,其余为欠阻尼(衰减振荡)情况,这时方程的解为：程序运行结果图7-1(b)电流iL的波形(方法Ⅰ)图7-2(a)电压uc的波形(方法Ⅱ)图7-2(b)电流iL的波形(方法Ⅱ)