
序贯决策博弈.pptx

胜利****实阿






亲,该文档总共86页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

序贯决策博弈.pptx
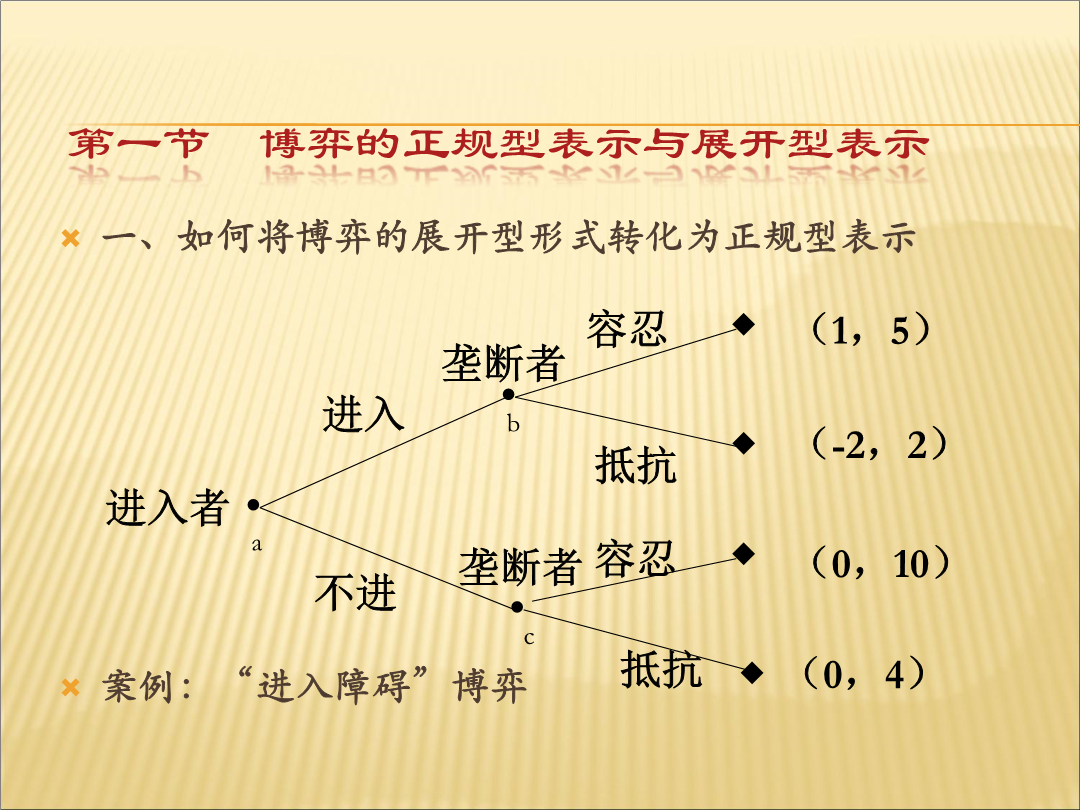
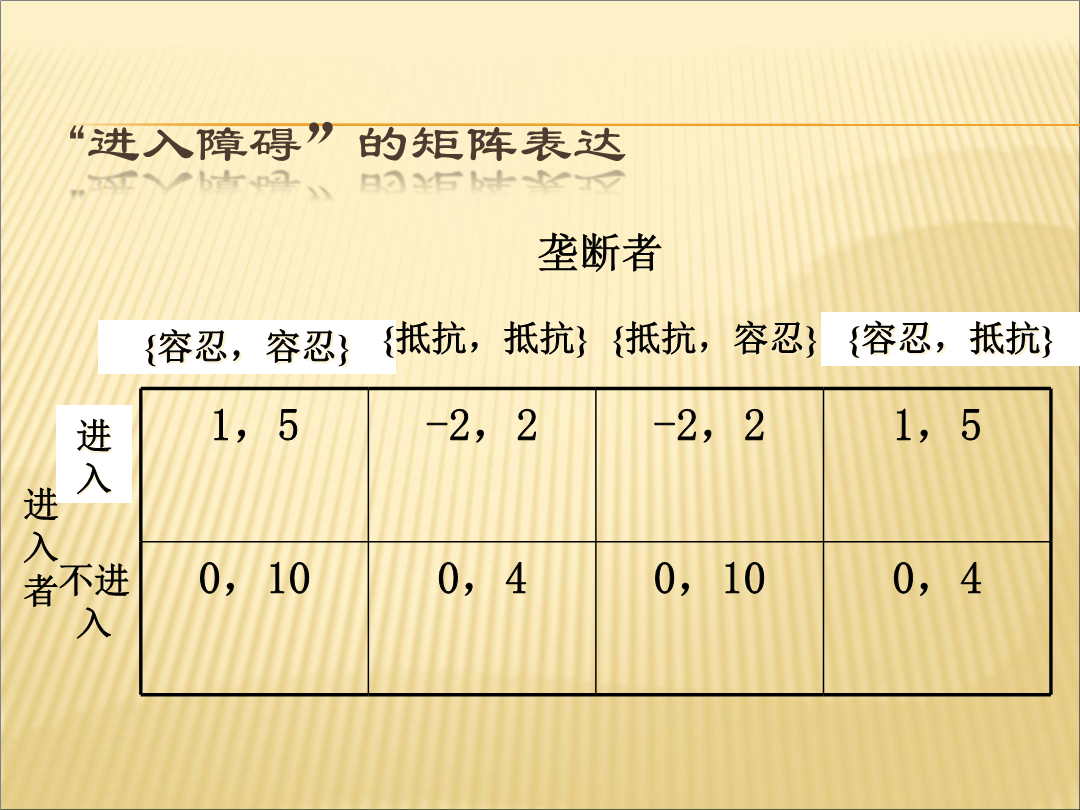
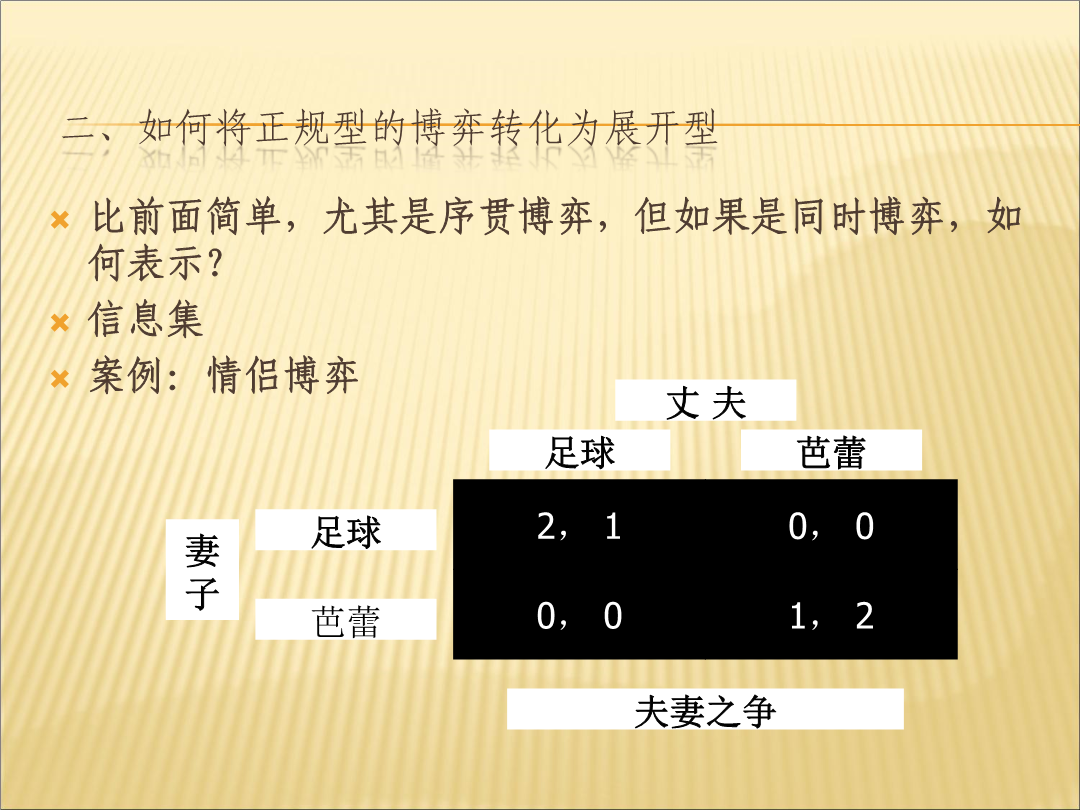
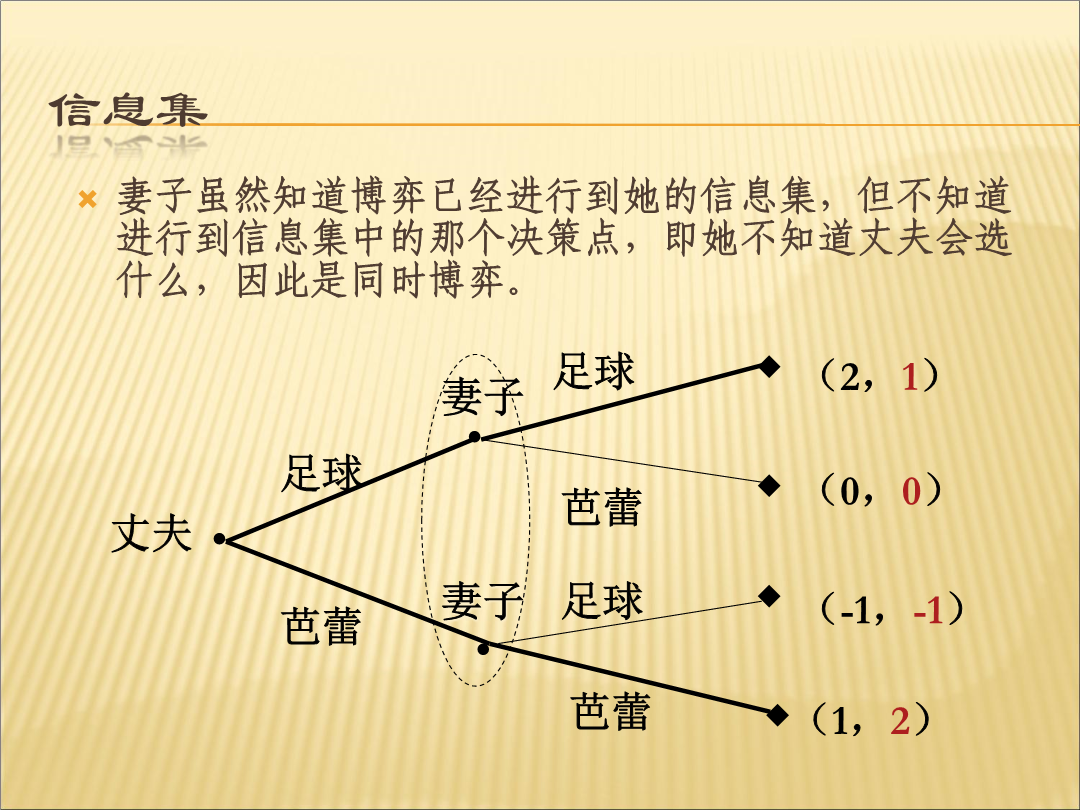
序贯决策博弈第一部分同时博弈与序贯博弈主要内容第一节博弈的正规型表示与展开型表示第二节同时决策与序贯决策的混合博弈第三节树形博弈的子博弈第四节子博弈精炼纳什均衡第五节完美博弈的库恩定理第六节动态博弈的运用第一节博弈的正规型表示与展开型表示“进入障碍”的矩阵表达小结二、如何将正规型的博弈转化为展开型信息集信息集注意注意单点集和非单点集完美信息博弈和不完美信息博弈信息集举例情爱博弈的扩展式表述第二节同时决策与序贯决策的混合博弈(完全不完美信息的两阶段博弈)联想联想联想银行挤兑博弈案例两个投资者的提款日期可以有

序贯决策博弈.pptx
序贯决策博弈第一部分同时博弈与序贯博弈主要内容第一节博弈的正规型表示与展开型表示第二节同时决策与序贯决策的混合博弈第三节树形博弈的子博弈第四节子博弈精炼纳什均衡第五节完美博弈的库恩定理第六节动态博弈的运用第一节博弈的正规型表示与展开型表示“进入障碍”的矩阵表达小结二、如何将正规型的博弈转化为展开型信息集信息集注意注意单点集和非单点集完美信息博弈和不完美信息博弈信息集举例情爱博弈的扩展式表述第二节同时决策与序贯决策的混合博弈(完全不完美信息的两阶段博弈)联想联想联想银行挤兑博弈案例两个投资者的提款日期可以有

序贯决策博弈概述.pptx
第四章序贯决策博弈实验:枪手博弈1实验:枪手博弈2实验:海盗分宝本章讨论动态博弈,所有博弈方都对博弈过程和得益完全了解的完全且完美信息动态博弈。这类博弈也是现实中常见的基本博弈类型。由于动态博弈中博弈方的选择、行为有先后次序,因此在表示方法、利益关系、分析方法和均衡概念等方面,都与静态博弈有很大区别。本章对动态博弈分析的概念和方法,特别是子博弈完美均衡和逆推归纳法作系统介绍,并介绍各种经典的动态博弈模型。主要内容一、序贯博弈的定义和表示方法博弈树进入障碍博弈“进入者”和“垄断者”的纯策略行动与策略策略组合
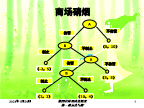
序贯决策博弈培训课件.pptx
2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年1月29日2024年

序贯决策博弈相关资料.pptx
第四章序贯决策博弈本章讨论动态博弈,所有博弈方都对博弈过程和得益完全了解的完全且完美信息动态博弈。这类博弈也是现实中常见的基本博弈类型。由于动态博弈中博弈方的选择、行为有先后次序,因此在表示方法、利益关系、分析方法和均衡概念等方面,都与静态博弈有很大区别。本章对动态博弈分析的概念和方法,特别是子博弈完美均衡和逆推归纳法作系统介绍,并介绍各种经典的动态博弈模型。主要内容一、序贯博弈的定义和表示方法博弈的三要素构造博弈战略式表述扩展式表述博弈博弈的扩展式表述——博弈树举例进入障碍博弈二、序贯博弈的纳什均衡策略
