
第6章虚拟仪器数据采集与信号处理ppt课件.ppt

胜利****实阿









亲,该文档总共69页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第6章虚拟仪器数据采集与信号处理ppt课件.ppt
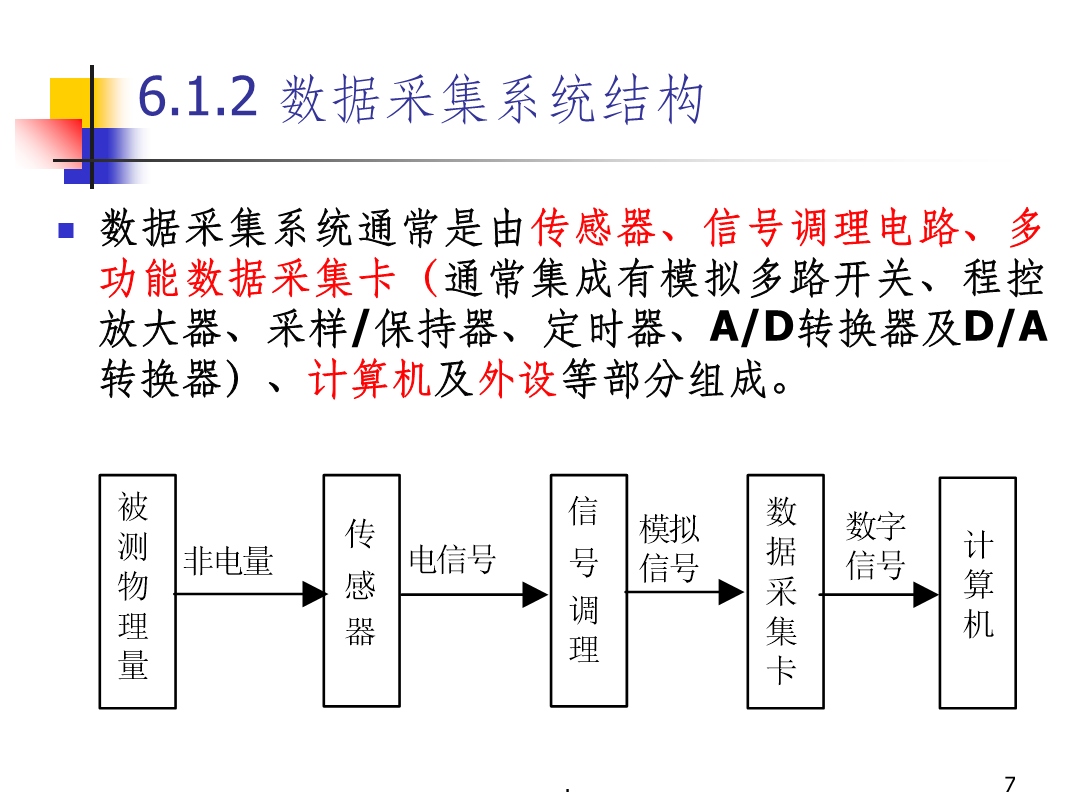
第6章第6章虚拟仪器数据采集与信号处理6.1数据采集6.1.1数据采集系统的含义6.1.2数据采集系统结构6.1.3数据采集卡的选用与配置数据采集卡的选用数据采集卡产品介绍数据采集卡的安装配置6.1.4基于LabVIEW的数据采集过程6.1.5基于LabVIEW的数据采集VI设计1.基于DAQ助手的数据采集2.基于DAQmx函数的数据采集连续数据采集多通道循环数据采集多通道循环数据采集(2)离散信号的采集6.2信号产生6.2.1数字信号的产生与数字化频率的概念6.2.2信号生成1.正弦波生成SineWav

第6章虚拟仪器数据采集与信号处理.ppt
第6章第6章虚拟仪器数据采集与信号处理6.1数据采集6.1.1数据采集系统的含义6.1.2数据采集系统结构6.1.3数据采集卡的选用与配置数据采集卡的选用数据采集卡产品介绍数据采集卡的安装配置6.1.4基于LabVIEW的数据采集过程6.1.5基于LabVIEW的数据采集VI设计1.基于DAQ助手的数据采集2.基于DAQmx函数的数据采集连续数据采集多通道循环数据采集多通道循环数据采集(2)离散信号的采集6.2信号产生6.2.1数字信号的产生与数字化频率的概念6.2.2信号生成1.正弦波生成SineWav

基于虚拟仪器的高频信号采集与数据分析.docx
基于虚拟仪器的高频信号采集与数据分析随着科技的不断发展和进步,虚拟仪器成为了高频信号采集与数据分析的重要工具。在过去,高频信号采集和分析是通过传统的仪器来完成的,这些仪器需要大量的时间和成本来进行调试和校准。而虚拟仪器可以极大的简化这些过程,使得工作效率和耗费成本都得到了很大程度的提高。一、虚拟仪器的基本概念虚拟仪器是实验室测试仪器与计算机技术的融合,它采用了软件化的方法来实现传统仪器的功能,适用于各种测试环境。虚拟仪器由信号源、传感器、数据采集卡、分析软件等组件组成。信号源提供测试信号,传感器收集响应信

虚拟仪器——DAQ采集ppt课件.ppt
第8章数据采集学习目标8.1概述LabVIEW的数据采集(DataAcquisition)程序库包括了许多NI公司数据采集(DAQ)卡的驱动控制程序。通常,一块卡可以完成多种功能-模/数转换,数/模转换,数字量输入/输出,以及计数器/定时器操作等。用户在使用之前必须对DAQ卡的硬件进行配置。这些控制程序用到了许多低层的DAQ驱动程序。DAQ系统的基本任务是物理信号的产生或测量。但是要使计算机系统能够测量物理信号,必须要使用传感器把物理信号转换成电信号(电压或者电流信号)。有时不能把被测信号直接连接到DAQ

虚拟仪器——DAQ采集ppt课件.ppt
第8章数据采集学习目标8.1概述LabVIEW的数据采集(DataAcquisition)程序库包括了许多NI公司数据采集(DAQ)卡的驱动控制程序。通常,一块卡可以完成多种功能-模/数转换,数/模转换,数字量输入/输出,以及计数器/定时器操作等。用户在使用之前必须对DAQ卡的硬件进行配置。这些控制程序用到了许多低层的DAQ驱动程序。DAQ系统的基本任务是物理信号的产生或测量。但是要使计算机系统能够测量物理信号,必须要使用传感器把物理信号转换成电信号(电压或者电流信号)。有时不能把被测信号直接连接到DAQ
