计算机系统概述优选ppt资料.ppt

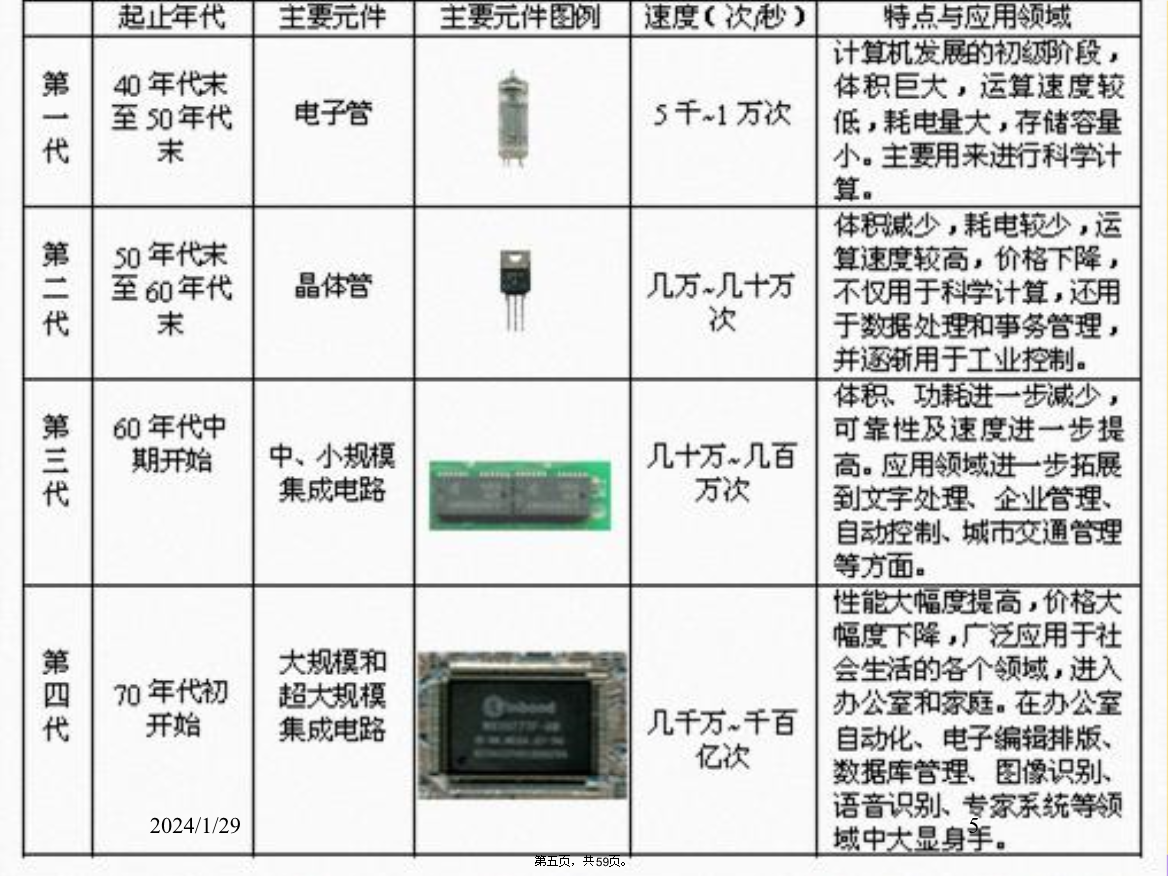
计算机系统概述(ɡàishù)计算机概述(ɡàishù)1.1.1计算机的发展(fāzhǎn)2、计算机的发展历程在计算机的发展过程中，逻辑元件（电子器件）的发展起到了决定性作用，它是计算机换代的主要标志。人们依据计算机所采用的电子器件，将分成(fēnchénɡ)四代。第一代——电子管计算机（1946~1957年）第二代——晶体管计算机（1958~1964年）第三代——小规模、中规模集成电路计算机（1965~1970年）第四代——大规模、超大规模集成电路计算机（1971年至今）新一代计算机(第五代)：新型智能化计算机(尚未研制出)第五页，。未来(wèilái)新型计算机2．生物计算机生物计算机又称仿生计算机，是以生物芯片取代在半导体硅片上集成效以万计的晶体管制成的计算机。它的主要原材料是生物工程技术产生的蛋白质分子，并以此(yǐcǐ)作为生物芯片。优点：体积小，功效高。（在一平方毫米的面积上，可容纳几亿个电路，比目前的集成电路小得多）生物计算机具有永久性和很高的可靠性。（内部芯片出现故障时，不需要人工修理，能自我修复）生物计算机芯片本身还具有并行处理的功能，其运算速度要比当今最新一代的计算机快10万倍。能量消耗小，仅相当于普通计算机的十亿分之一。存储信息的空间小，仅占百亿亿分之一。第九页，。3．量子计算机量子计算机（quantumcomputer）是一类遵循量子力学规律进行高速数学和逻辑运算、存储及处理量子信息的物理装置。当某个装置处理和计算的是量子信息，运行的是量子算法时，它就是量子计算机。优点：高效率缺点：能量消耗大，产生热量(rèliàng)大，寿命短。主要用途是例如像测量星体精确坐标、快速计算不规则立体图形体积、精确控制机器人等需要大规模、高精度的高速浮点运算的工作。2007年第一台商业化的量子计算机在加拿大计算机公司D-Wave产生。第十一页，。1.1.2微型(wēixíng)计算机的发展第十三页，。1.1.3计算机的特点(tèdiǎn)1.1.4计算机的分类(fēnlèi)1.1.5计算机的应用(yìngyòng)3.过程控制过程控制又称实时控制，是指将计算机对生产或其他过程中所采集到的数据按照一定的算法处理，然后反馈到执行机构去控制相应过程，是生产自动化的重要技术和手段。4.计算机辅助系统（1）CAD（ComputerAidedDesign，计算机辅助设计）（2）CAM（ComputerAidedManufacturing，计算机辅助制造）（3）CBE（ComputerBasedEducation，计算机辅助教育(jiàoyù)）：包括CAI（ComputerAidedInstruction，计算机辅助教学）、CAT（ComputerAidedTesting，计算机辅助测试）、CMI（ComputerManagedInstruction，计算机辅助管理教学）等。5.人工智能人工智能（AI——ArtificialIntelligence）是用计算机软、硬件系统模拟人的高级思维活动(如感知、推理、学习、理解等)的理论和技术。例如：语言(yǔyán)识别、模式识别、图像识别、专家系统、机器人等。6.多媒体及网络1.2计算机中的数制与编码(biānmǎ)1.2.1进位(jìnwèi)记数制度进制的基本要素：1.数码(shùmǎ)表示一个数位所使用的数字符号被称为数码(shùmǎ)。例如，十进制中使用的0，1，2，3，…，9都是数码(shùmǎ)。2.基数一种数制所使用的数码(shùmǎ)符号的个数称为该数制的基数。R进制的基数为R。例如，十进制允许使用0～9这十个数码(shùmǎ)，因此十进制的基数就为10。3.位权某个数位的单位称为该数位的位权（例如，在十进制中，个位、十位、百位的单位分别为个、十、百，因此个位、十位、百位的位权分别为100、101、102）。4.借进位规则有关进行加法（或乘法）运算，达到多少值需向高位进位“1”，进行减法（或除法(chúfǎ)）运算，何时需从高位借“1”，借来的“1”在本位当成几的运算规则，称为借进位规则。同一种进制的所有数位都应遵从统一的借进位规则。这就是“逢基数进一，借一当基数”。例如，十进制的基数为十，因此它的借进位规则是“逢十进一，借一当十”5.按权展开式按权展开式可以表述(biǎoshù)如下：例1.1写出按权展开(zhǎnkāi)十进制数的表达式。9876.54=9×103＋8×102＋7×101＋6×100＋5×10－1＋4×10－2。例1.2写出按权展开(zhǎnkāi)二进制数的多项式。（）2=1×25＋1×24＋1×23＋0×22＋1×21＋1×20＋1×2－1＋0×2－2＋1×2－3＋0×2－41.2.2计算机中常用(chánɡyònɡ)的几种记数制在计算机内部，