
matlab人口预测与数据曲线拟合.ppt

胜利****实阿







亲,该文档总共35页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

matlab人口预测与数据曲线拟合.ppt
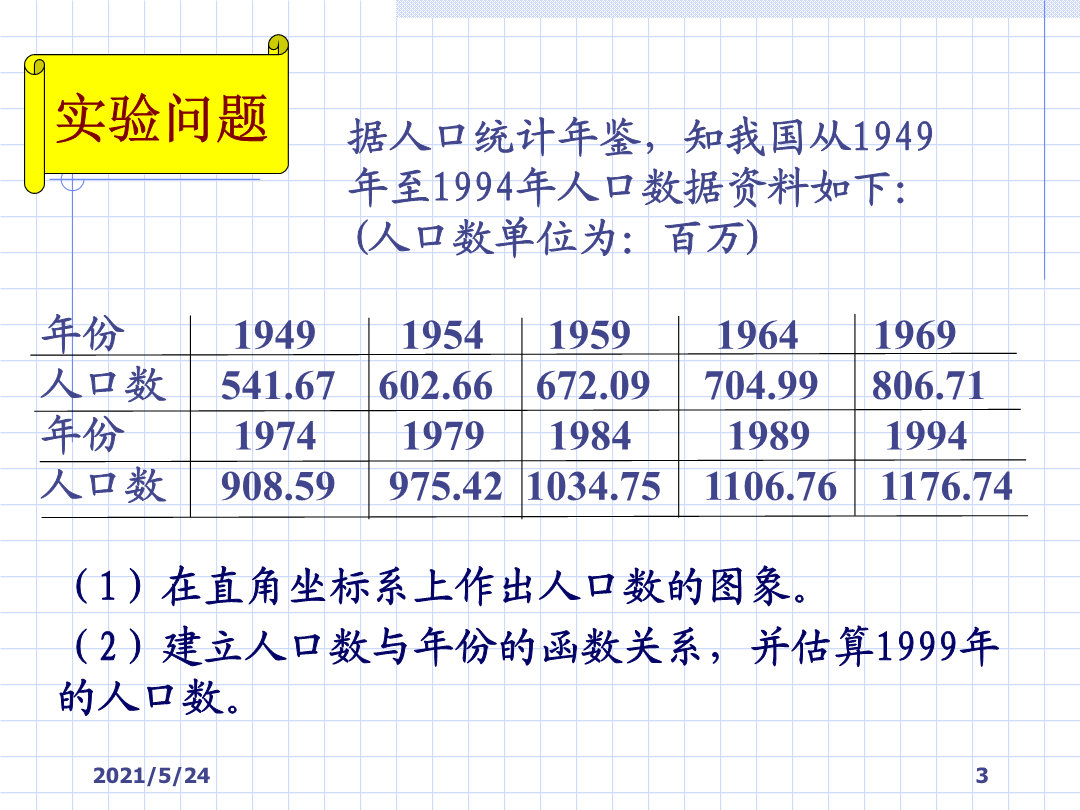
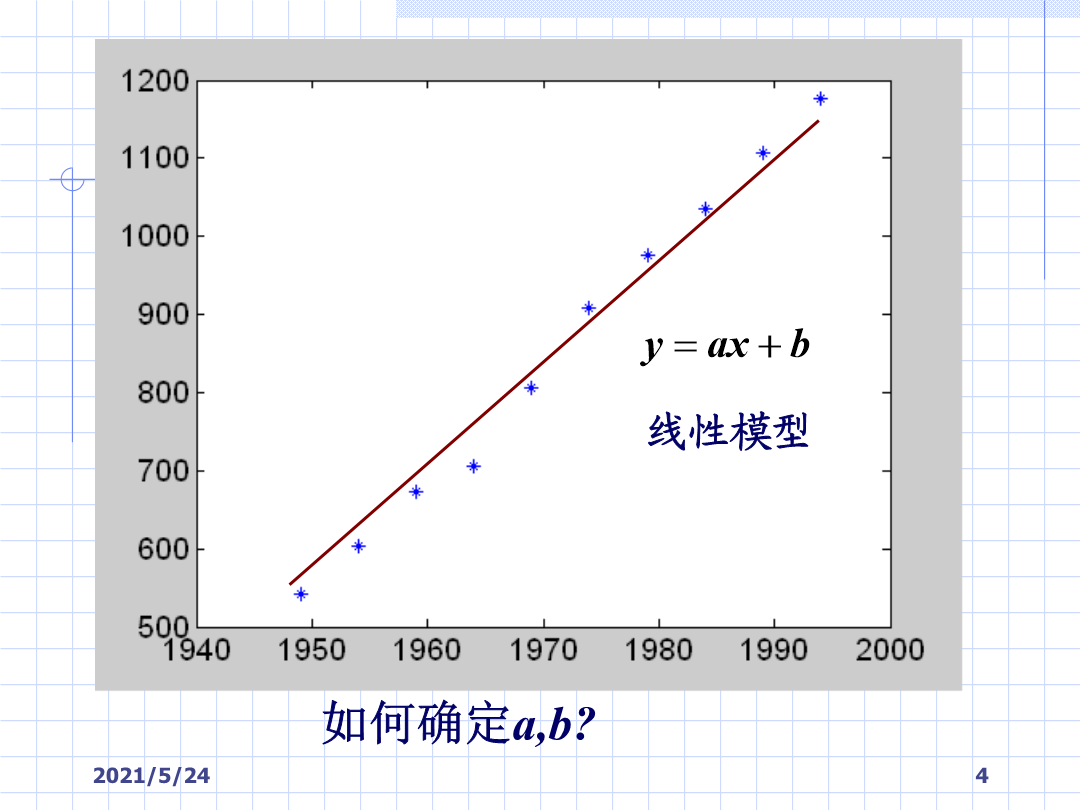
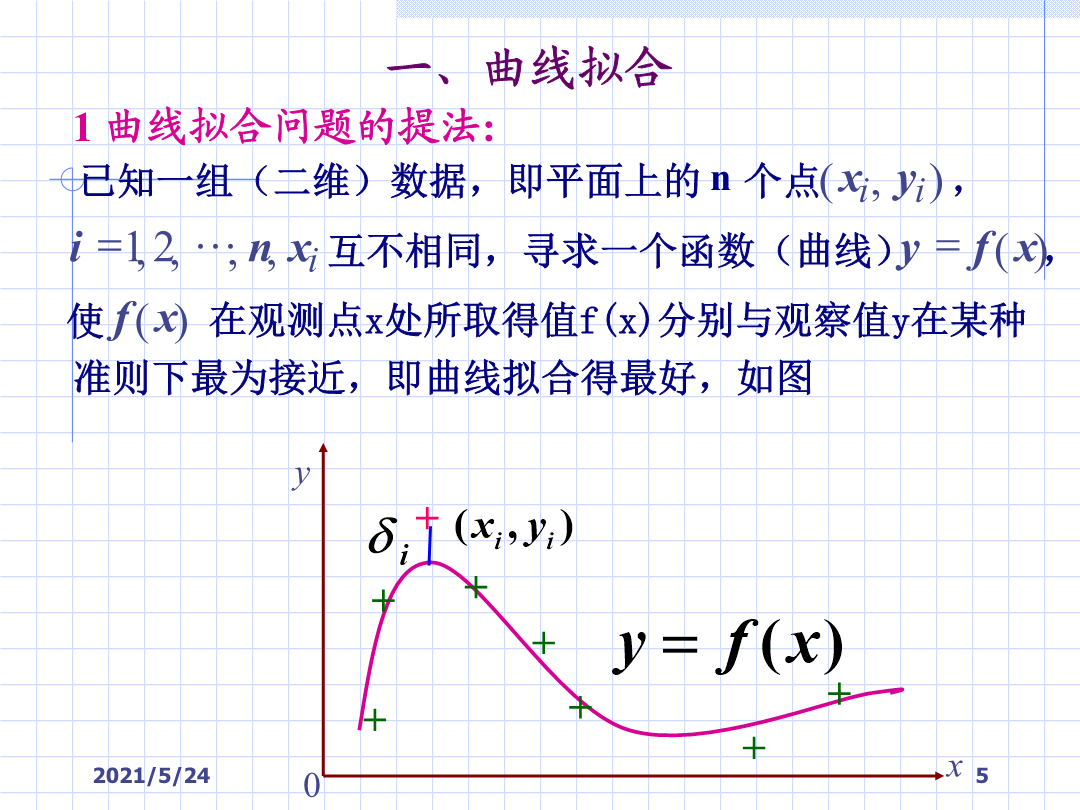
实验13人口预测与数据拟合据人口统计年鉴,知我国从1949年至1994年人口数据资料如下:(人口数单位为:百万)如何确定a,b?1曲线拟合问题的提法:从几何上讲,并不要求曲线严格通过已知点,但要求曲线在各数据点和已知数据点之间的总体误差最小,通常称为数据拟合。数据插值2.用什么样的曲线拟合已知数据?例如3拟合函数组中系数的确定4用matlab软件进行数据拟合例也可以用inline命令定义函数a=polyfit(xdata,ydata,n)其中n表示多项式的最高阶数xdata,ydata为要拟合的数据,它是

matlab人口预测与数据曲线拟合.ppt
实验13人口预测与数据拟合据人口统计年鉴,知我国从1949年至1994年人口数据资料如下:(人口数单位为:百万)如何确定a,b?1曲线拟合问题的提法:从几何上讲,并不要求曲线严格通过已知点,但要求曲线在各数据点和已知数据点之间的总体误差最小,通常称为数据拟合。数据插值2.用什么样的曲线拟合已知数据?例如3拟合函数组中系数的确定4用matlab软件进行数据拟合例也可以用inline命令定义函数a=polyfit(xdata,ydata,n)其中n表示多项式的最高阶数xdata,ydata为要拟合的数据,它是

基于MATLAB的数据曲线拟合.docx
基于MATLAB的数据曲线拟合近年来,数据曲线拟合技术在科研领域中发挥着愈加重要的作用。在生物科学、工程学、医学等领域都需要精确的曲线拟合来进行数据分析和研究。因此,数据曲线拟合技术已成为一个热门的研究领域。本文将介绍基于MATLAB的数据曲线拟合。MATLAB是一种专门用于数学计算和科学工程的高级编程语言。它提供了实用的算法和工具箱,使得数据分析和曲线拟合变得更加便捷和高效。在MATLAB中,数据曲线拟合通常包括以下几个步骤:1.数据处理与预处理在进行曲线拟合之前,需要对原始数据进行处理和预处理。这些处

人口预测和数据曲线拟合公开课获奖课件.pptx
试验13人口预测与数据拟合据人口记录年鉴,知我国从1949年至1994年人口数据资料如下:(人口数单位为:百万)怎样确定a,b?1曲线拟合问题提法:从几何上讲,并不规定曲线严格通过已知点,但规定曲线在各数据点和已知数据点之间总体误差最小,一般称为数据拟合。数据插值2.用什么样曲线拟合已知数据?例如3拟合函数组中系数确定4用matlab软件进行数据拟合例也可以用inline命令定义函数a=polyfit(xdata,ydata,n)其中n表达多项式最高阶数xdata,ydata为要拟合数据,它是用向量方式输

基于MATLAB的人口预测模型.doc
基于MATLAB的人口预测模型摘要本文以1980—2014年中国年终总人口数据资料为依据,分别使用了一次拟合、灰色预测模型和时间序列模型进行拟合,最终得出时间序列模型的效果最优,得到了中国人口数量逐年增长,但同时增长速度逐渐放缓的结论,为政府制定人口、经济政策提供了一定的依据。关键词:人口数量;一次拟合;灰色预测;时间序列前言世界人口的迅猛增长引起了许多问题。特别是一些经济不发达国家的人口过度增长,影响了整个国家的经济发展、社会安定和人民生活水平的提高,给人类生活带来许多问题.为了解决人口增长过快的问题,
