
基于Gibbs抽样的贝叶斯随机波动模型分析.pdf

代瑶****zy






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

基于Gibbs抽样的贝叶斯随机波动模型分析.pdf
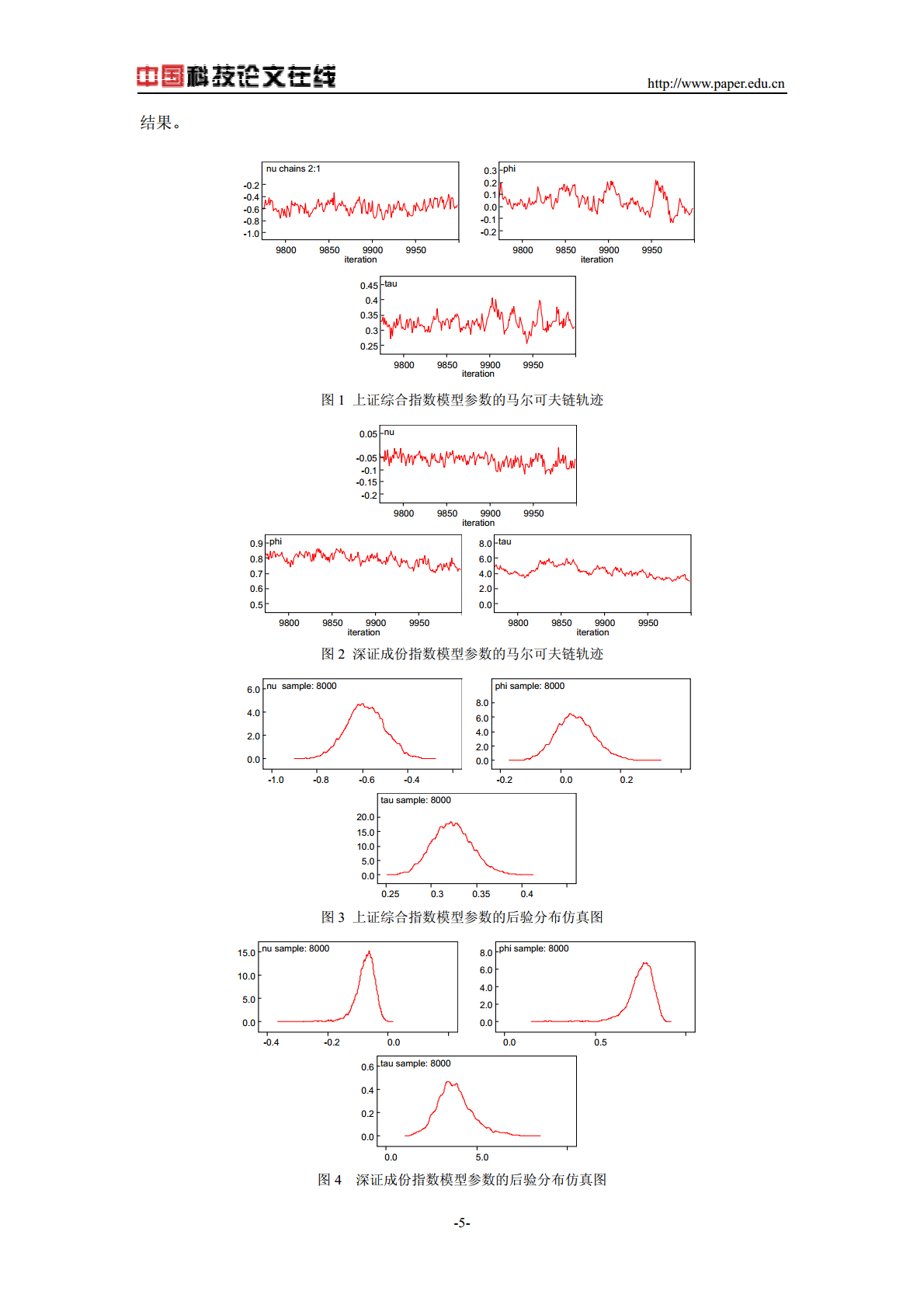
http://www.paper.edu.cn基于Gibbs抽样的贝叶斯随机波动模型分析1朱慧明赵锐郝立亚湖南大学统计学院长沙(410079)摘要:随机波动性是经济金融时间序列中的一个普遍现象它在金融风险管理研究中具有重要地位。通过分析随机波动

基于Gibbs抽样算法的贝叶斯动态面板数据模型分析.docx
基于Gibbs抽样算法的贝叶斯动态面板数据模型分析摘要:本文基于Gibbs抽样算法,对贝叶斯动态面板数据模型进行分析。首先对贝叶斯统计学和面板数据模型进行简要介绍,然后利用Gibbs抽样算法对模型的参数进行估计,最后通过实证研究考察该模型的可行性和预测效果。关键词:Gibbs抽样算法;贝叶斯动态面板数据模型;参数估计;预测1.引言动态面板数据模型常用于对经济学、金融学、社会科学等领域的长期发展进行研究和预测。通常情况下,该模型基于固定效应或者随机效应模型,通过解析和计算得到相关模型的系数和参数,从而预测模

基于Gibbs抽样的贝叶斯模型选择及其应用的中期报告.docx
基于Gibbs抽样的贝叶斯模型选择及其应用的中期报告一、研究背景Bayesianmodelselection是一类经典的贝叶斯统计模型,它常用于在多个竞争模型之间进行选择和比较。传统的Bayesianmodelselection方法通常采用较为复杂的模型组合优化方法,难以实现。近年来,基于Gibbs抽样的Bayesianmodelselection方法在模型选择领域被广泛应用,具有计算简单、易于实现等优点。二、研究内容本研究主要围绕基于Gibbs抽样的Bayesianmodelselection方法展开,

基于贝叶斯随机波动模型的短期风速预测.docx
基于贝叶斯随机波动模型的短期风速预测摘要:本文以贝叶斯随机波动模型为基础,探讨了短期风速预测的方法。首先介绍了市场对风能的需求和风电站的重要性,然后分析了短期风速预测的难点和现有的一些方法的局限性。接着,介绍了贝叶斯随机波动模型的原理和特点,并讨论了如何将其应用于短期风速预测。最后,通过实例分析,证明了贝叶斯随机波动模型在短期风速预测中的有效性。关键词:短期风速预测;贝叶斯随机波动模型;风电站;风能;市场需求。1.引言随着全球对清洁能源的需求不断增加,风电站作为其中的重要组成部分,受到越来越多的关注。而要

基于贝叶斯理论的随机波动模型参数估计方法研究.docx
基于贝叶斯理论的随机波动模型参数估计方法研究基于贝叶斯理论的随机波动模型参数估计方法研究摘要:随机波动模型是金融领域中广泛使用的模型之一,用于描述资产价格的随机变动。参数估计是确定模型的关键步骤之一。传统的参数估计方法存在一些问题,无法充分考虑先验信息以及参数的不确定性。本文基于贝叶斯理论,提出了一种新的随机波动模型参数估计方法。通过引入先验分布和后验分布,能够更准确地估计参数,并考虑到参数的不确定性。实证结果表明,该方法能够有效提高参数估计的准确性和稳定性。关键词:随机波动模型,贝叶斯理论,参数估计,先
