
第十章基础资产价格的变动_随机微分方程.ppt

猫巷****熙柔








亲,该文档总共37页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

基础资产价格的变动-随机微分方程.pptx
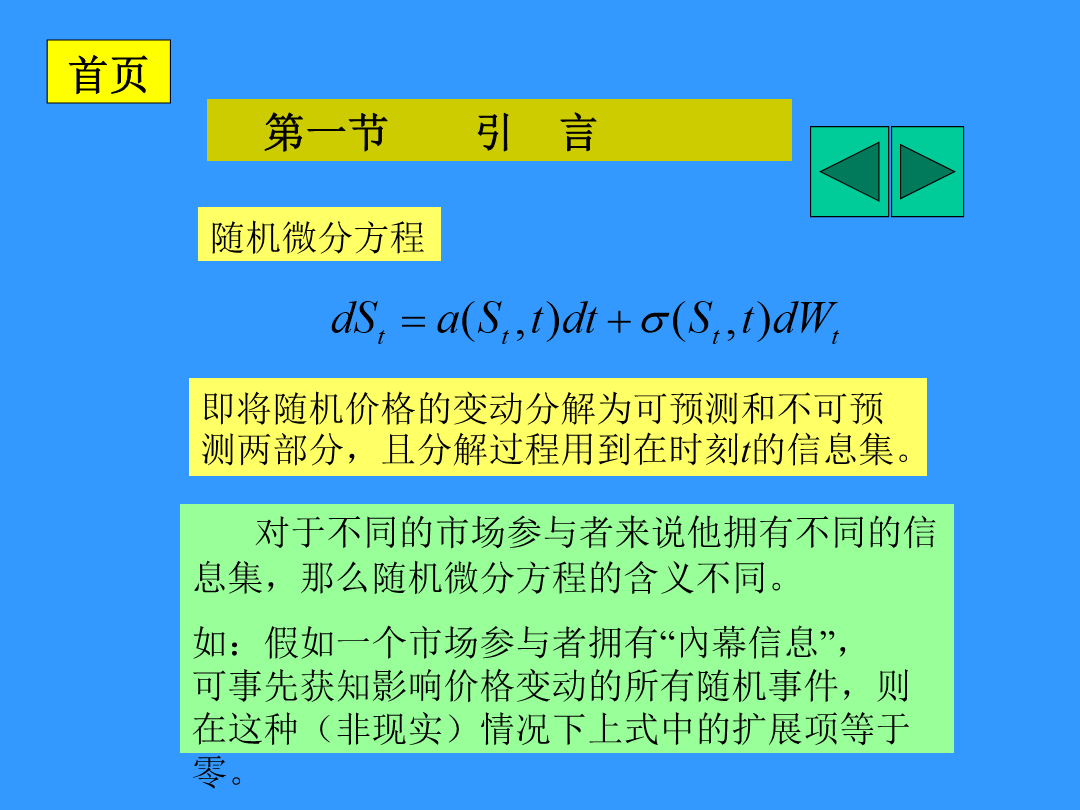
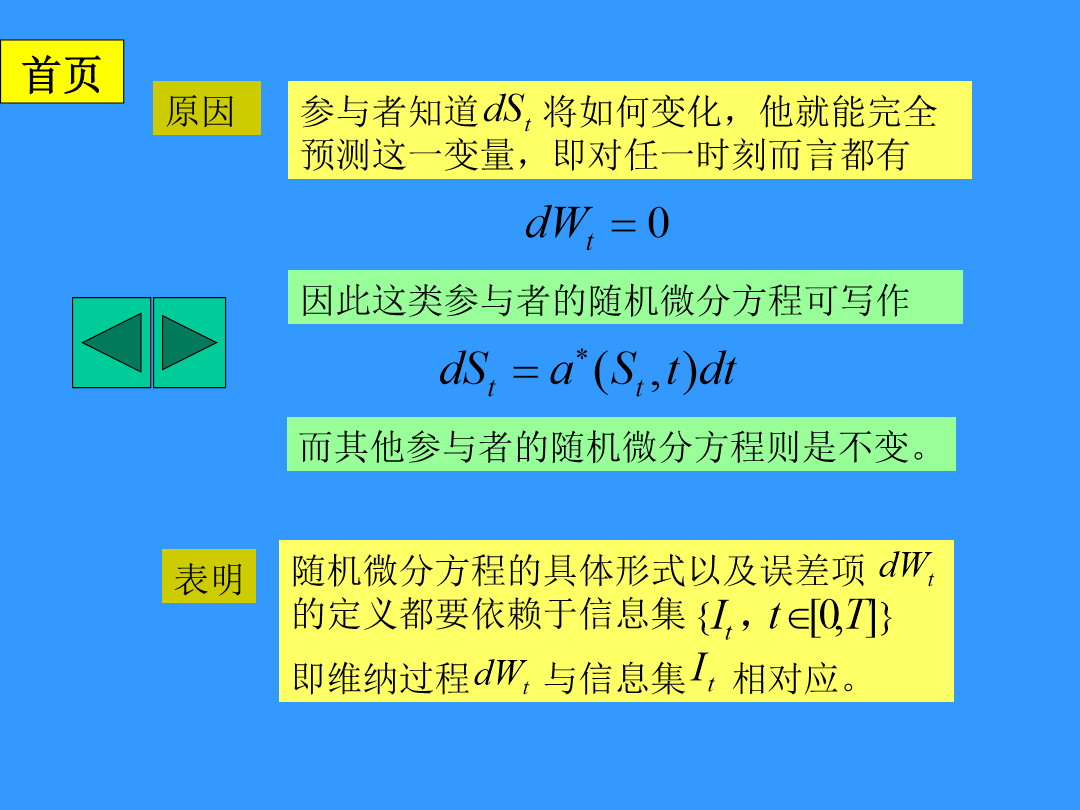
第九章基础资产价格的变动-------随机微分方程第一节引言随机微分方程的具体形式以及误差项的定义都要依赖于信息集随机微分方程可用于对衍生金融资产定价的原因随机微分方程模型一般条件第二节随机微分方程的求解观察在很短的且不连续的时间间隔上的有限差再寻求当时间间隔h趋于0时的方程的解则随机过程:2.弱解与的区别其中的扩展项包含外生变量,它表示影响价格进行完全不可预测变动的极其微小的事件。这一系列小事件形成的“历史”就是t时刻的信息集。强解和弱解具有相同的主项和扩展项,因此和具有相似的统计特性。给定均值和方差,

基础资产价格的变动—随机微分方程.ppt
第九章基础资产价格的变动-------随机微分方程第一节引言随机微分方程的具体形式以及误差项的定义都要依赖于信息集随机微分方程可用于对衍生金融资产定价的原因随机微分方程模型一般条件第二节随机微分方程的求解观察在很短的且不连续的时间间隔上的有限差再寻求当时间间隔h趋于0时的方程的解则随机过程:2.弱解与的区别其中的扩展项包含外生变量,它表示影响价格进行完全不可预测变动的极其微小的事件。这一系列小事件形成的“历史”就是t时刻的信息集。强解和弱解具有相同的主项和扩展项,因此和具有相似的统计特性。给定均值和方差,

第十章基础资产价格的变动_随机微分方程.ppt
第九章基础资产价格的变动-------随机微分方程第一节引言随机微分方程的具体形式以及误差项的定义都要依赖于信息集随机微分方程可用于对衍生金融资产定价的原因随机微分方程模型一般条件第二节随机微分方程的求解观察在很短的且不连续的时间间隔上的有限差再寻求当时间间隔h趋于0时的方程的解则随机过程:2.弱解与的区别其中的扩展项包含外生变量

第十章基础资产价格的变动_随机微分方程.ppt
第九章基础资产价格的变动-------随机微分方程第一节引言随机微分方程的具体形式以及误差项的定义都要依赖于信息集随机微分方程可用于对衍生金融资产定价的原因随机微分方程模型一般条件第二节随机微分方程的求解观察在很短的且不连续的时间间隔上的有限差再寻求当时间间隔h趋于0时的方程的解则随机过程:2.弱解与的区别其中的扩展项包含外生变量

宏观经济与资产价格的变动关系.doc
宏观经济与资产价格的变动关系房价下跌和次贷危机,已经导致了贝尔斯登、美林证券、房利美、房地美、雷曼兄弟等投行和金融机构或倒闭或被收购、接管,美国金融危机逐步加深并向其他国家蔓延,并愈演愈烈。随着金融全球化的加深,此次危机已经影响到其他国家的金融市场稳定。我国经济正面临着来自于国际国内的诸多不确定因素的挑战,宏观经济也出现下滑的迹象。在宏观经济走势不明朗的背景下,我国的债券市场却一枝独秀,尤其是企业债更是表现优异。本文通过对债券影响因素的分析,旨在试着寻找当前宏观经济走势下我国企业债券市场繁荣的原因。一、影
