
53 运输问题的求解方法.pptx

骊蓉****23







亲,该文档总共35页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

53 运输问题的求解方法.pptx
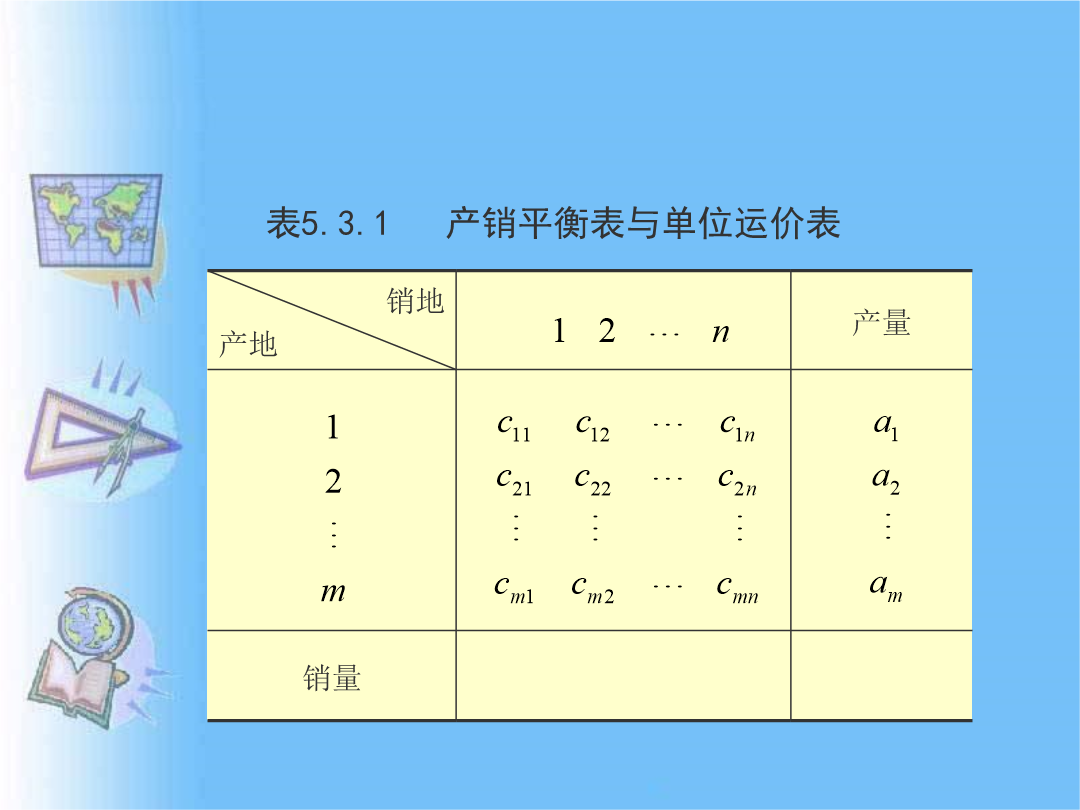
第3节运输问题的求解方法——表上作业法一、产销平衡表与单位运价表运输问题还可用产销平衡表与单位运价表进行描述。假设某种物资有m个生产地点Ai(i=12…m)其产量(供应量)分别为ai(i=12…m)有n个销地Bj(j=12…n)其销量(需求量)分别为bj(j=12…n)。从Ai到Bj运输单位物资的运价(单价)为Cij。将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。销地产地运输这一类特殊问题可用更加简便的求解方法———表上作业法求解实质仍是单纯形法

53 运输问题的求解方法.ppt
第3节运输问题的求解方法——表上作业法一、产销平衡表与单位运价表运输问题还可用产销平衡表与单位运价表进行描述。假设某种物资有m个生产地点Ai(i=12…m)其产量(供应量)分别为ai(i=12…m)有n个销地Bj(j=12…n)其销量(需求量)分别为bj(j=12…n)。从Ai到Bj运输单位物资的运价(单价)为Cij。将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。销地产地运输这一类特殊问题可用更加简便的求解方法———表上作业法求解实质仍是单纯形法

53 运输问题的求解方法.ppt
第3节运输问题的求解方法——表上作业法一、产销平衡表与单位运价表运输问题还可用产销平衡表与单位运价表进行描述。假设某种物资有m个生产地点Ai(i=12…m)其产量(供应量)分别为ai(i=12…m)有n个销地Bj(j=12…n)其销量(需求量)分别为bj(j=12…n)。从Ai到Bj运输单位物资的运价(单价)为Cij。将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。销地产地运输这一类特殊问题可用更加简便的求解方法———表上作业法求解实质仍是单纯形法

运输问题的求解方法.ppt
第3节运输问题的求解方法——表上作业法一、产销平衡表与单位运价表运输问题还可用产销平衡表与单位运价表进行描述。假设某种物资有m个生产地点Ai(i=12…m)其产量(供应量)分别为ai(i=12…m)有n个销地Bj(j=12…n)其销量(需求量)分别为bj(j=12…n)。从Ai到Bj运输单位物资的运价(单价)为Cij。将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。销地产地运输这一类特殊问题可用更加简便的求解方法———表上作业法求解实质仍是单纯形法

运输问题的求解方法.ppt
第3节运输问题的求解方法——表上作业法一、产销平衡表与单位运价表运输问题还可用产销平衡表与单位运价表进行描述。假设某种物资有m个生产地点Ai(i=12…m)其产量(供应量)分别为ai(i=12…m)有n个销地Bj(j=12…n)其销量(需求量)分别为bj(j=12…n)。从Ai到Bj运输单位物资的运价(单价)为Cij。将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。销地产地运输这一类特殊问题可用更加简便的求解方法———表上作业法求解实质仍是单纯形法
