
单自由度机械振动系统谐和力激励的受迫振动.pptx

一吃****海逸








亲,该文档总共65页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

单自由度机械振动系统谐和力激励的受迫振动.pptx
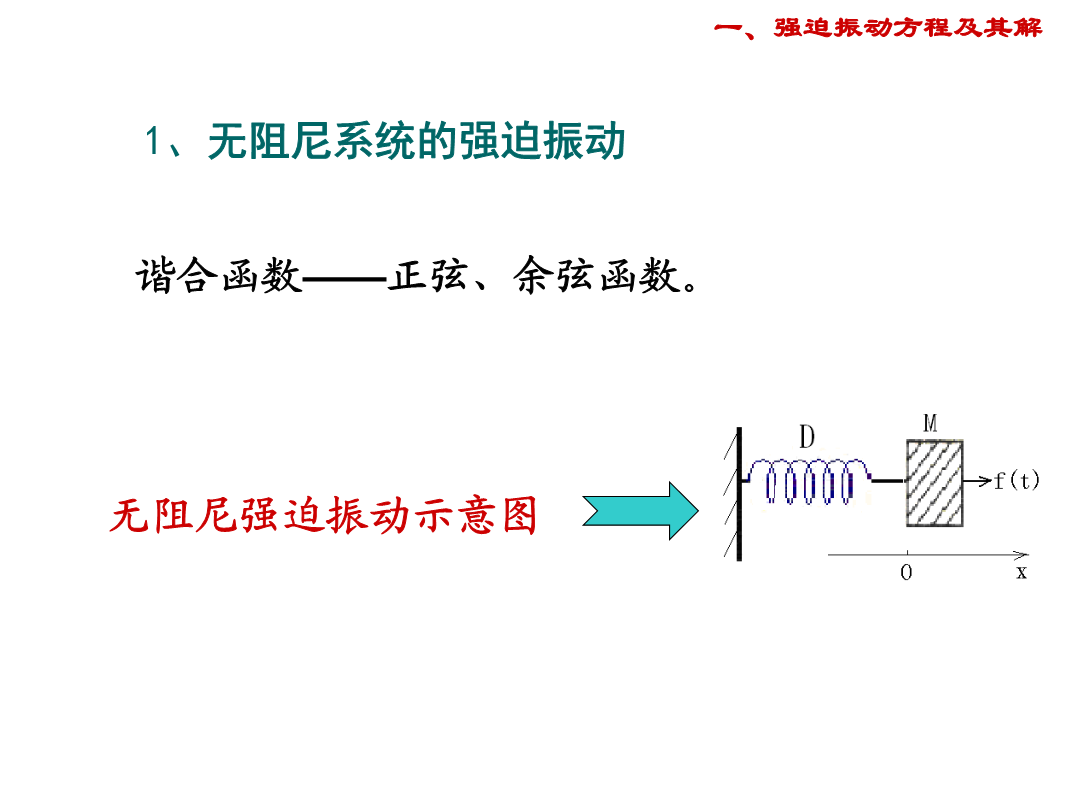
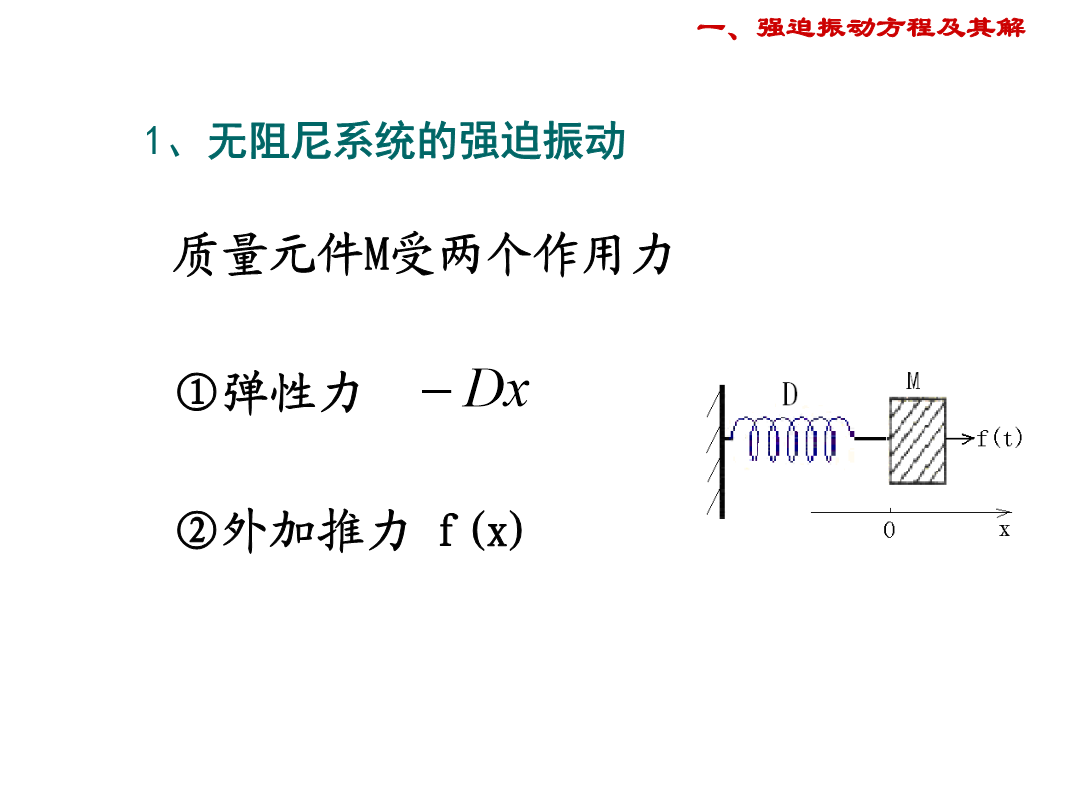
1.1.2单自由度机械振动系统谐和力激励的受迫振动内容提要一、强迫振动方程及其解无阻尼强迫振动示意图质量元件M受两个作用力①弹性力②外加推力f(x)运动方程式强迫振动方程是二阶的非齐次常微分方程其一般解应表示为该方程的一个特解与相应的齐次方程一般解之和。方程的解=一般解+特解据前方程(*)的通解为:设方程(*)特解的一般形式为得所以实际位移为:零初始条件的振动位移三角变换无阻尼系统的拍频振动规律①振动频率近似等于②“振幅”作慢周期变化拍周期当特例:当

单自由度机械振动系统谐和力激励的受迫振动培训课件.pptx
1.1.2单自由度机械振动系统谐和力激励的受迫振动内容提要一、强迫振动方程及其解无阻尼强迫振动示意图质量元件M受两个作用力①弹性力②外加推力f(x)运动方程式强迫振动方程是二阶的非齐次常微分方程其一般解应表示为该方程的一个特解与相应的齐次方程一般解之和。方程的解=一般解+特解据前方程(*)的通解为:设方程(*)特解的一般形式为得所以实际位移为:零初始条件的振动位移三角变换无阻尼系统的拍频振动规律①振动频率近似等于②“振幅”作慢周期变化拍周期当特例:当

单自由度系统受迫振动.ppt
1.3单自由度系统受迫振动微分方程的全解等于齐次方程的通解与非齐次方程的特解之和。有阻尼系统在简谐激励下,运动微分方程的全解特解为:幅频特性与相频特性结论:单自由度系统受迫振动/稳态响应的特性(2)当单自由度系统受迫振动/稳态响应的特性单自由度系统受迫振动/稳态响应的特性单自由度系统受迫振动/稳态响应的特性单自由度系统受迫振动/稳态响应的特性【例】图示带有偏心块的电动机,固定在一根不计自重的弹性梁上。设电机的质量为m1,偏心块的质量为m2,偏心距为e,弹性梁的刚度系数为k,阻力系数为c,求当电机以匀角速度

单自由度系统受迫振动.ppt
1.3单自由度系统受迫振动微分方程的全解等于齐次方程的通解与非齐次方程的特解之和。有阻尼系统在简谐激励下,运动微分方程的全解特解为:幅频特性与相频特性结论:单自由度系统受迫振动/稳态响应的特性(2)当单自由度系统受迫振动/稳态响应的特性单自由度系统受迫振动/稳态响应的特性单自由度系统受迫振动/稳态响应的特性单自由度系统受迫振动/稳态响应的特性【例】图示带有偏心块的电动机,固定在一根不计自重的弹性梁上。设电机的质量为m1,偏心块的质量为m2,偏心距为e,弹性梁的刚度系数为k,阻力系数为c,求当电机以匀角速度

单自由度系统受迫振动.ppt
单自由度系统受迫振动教学内容线性系统的受迫振动线性系统的受迫振动振动微分方程:振动微分方程:稳态响应的实振幅(1)线性系统对简谐激励的稳态响应是频率等同于激振频率、而相位滞后激振力的简谐振动线性系统的受迫振动稳态响应的特性稳态响应特性稳态响应特性稳态响应特性稳态响应特性稳态响应特性稳态响应特性稳态响应特性有阻尼单自由度系统线性系统的受迫振动受迫振动的过渡阶段受迫振动的过渡阶段初始条件响应初始条件响应初始条件为零时由于系统是线性的,也可利用叠加定理求解即使在零初始条件下,也有自由振动与受迫振动相伴发生例:例
