
教案-山东-2013_山东省文登市八年级数学下册 5.rar

慧颖****23


在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
教案-山东-2013_山东省文登市八年级数学下册 5.rar
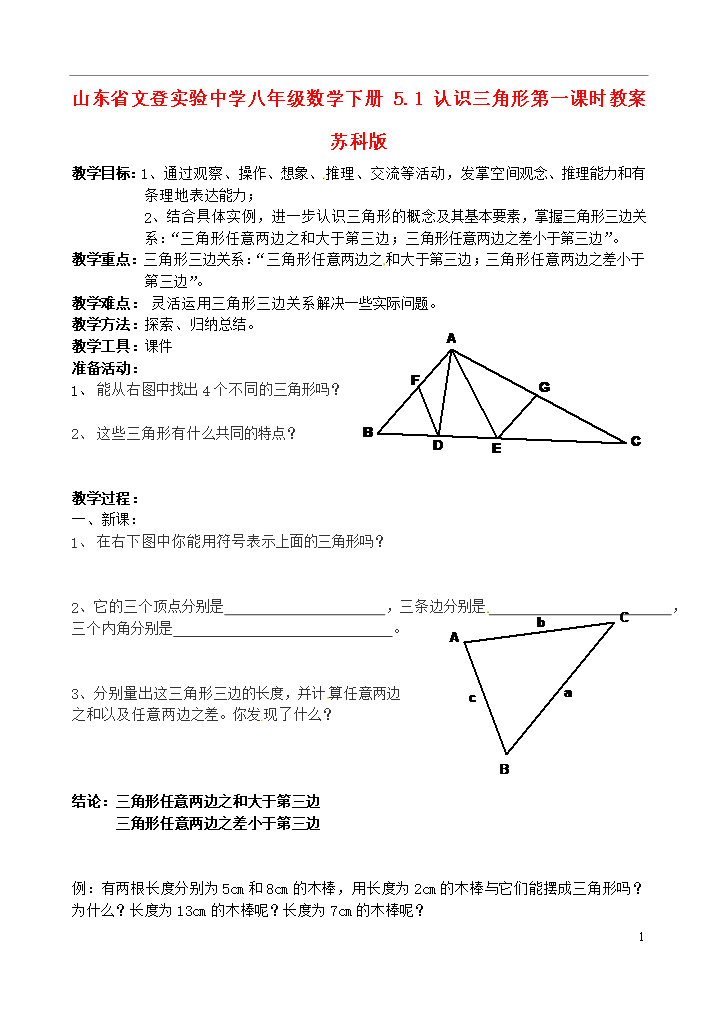
3山东省文登实验中学八年级数学下册5.1认识三角形第一课时教案苏科版教学目标:1、通过观察、操作、想象、推理、交流等活动,发掌空间观念、推理能力和有条理地表达能力;2、结合具体实例,进一步认识三角形的概念及其基本要素,掌握三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。教学重点:三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。教学难点:灵活运用三角形三边关系解决一些实际问题。教学方法:探索、归纳总结。教学工具:课件准备活动:能从右图中找出4个

教案-山东-2013_山东省文登市八年级数学下册 5.rar
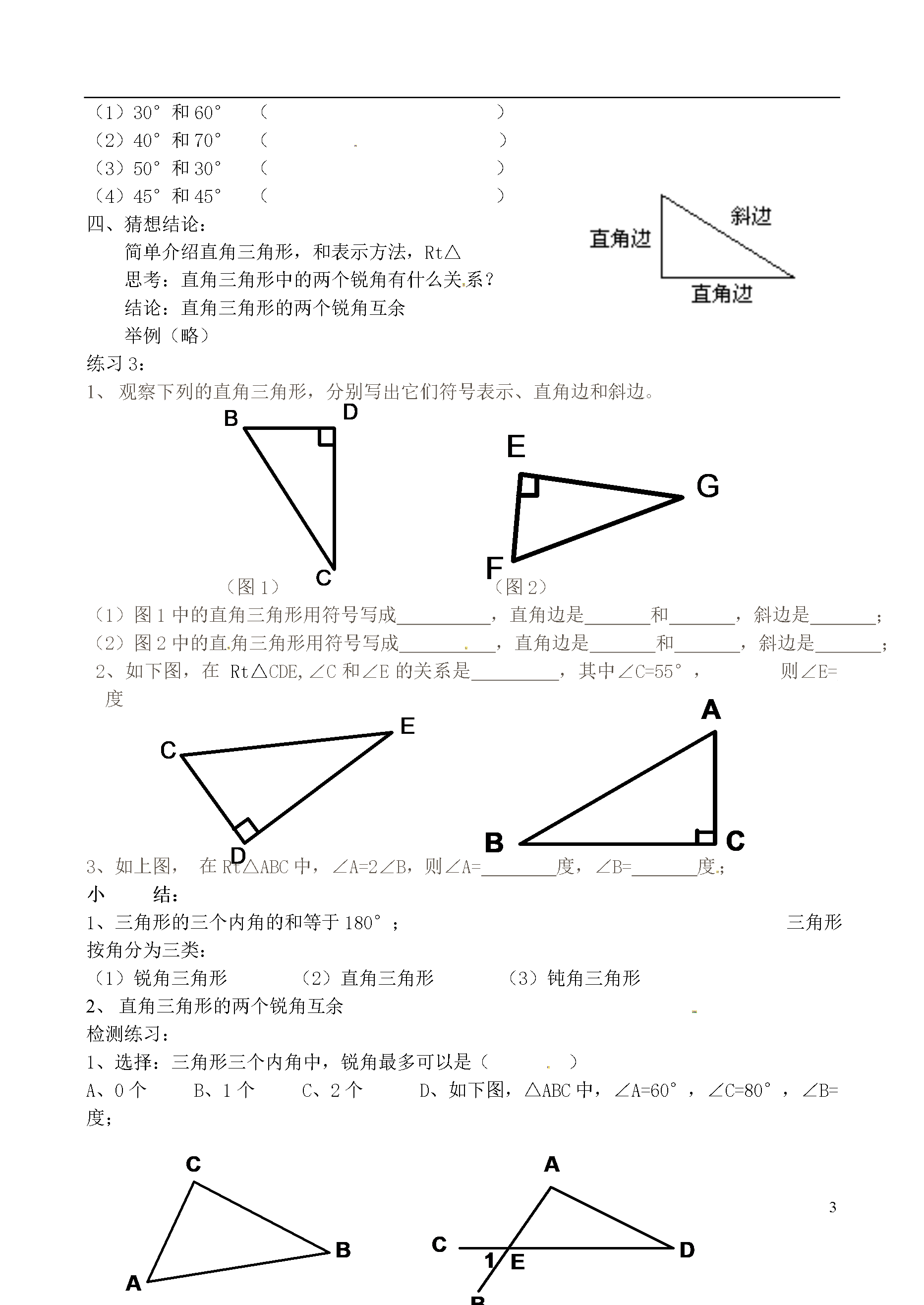
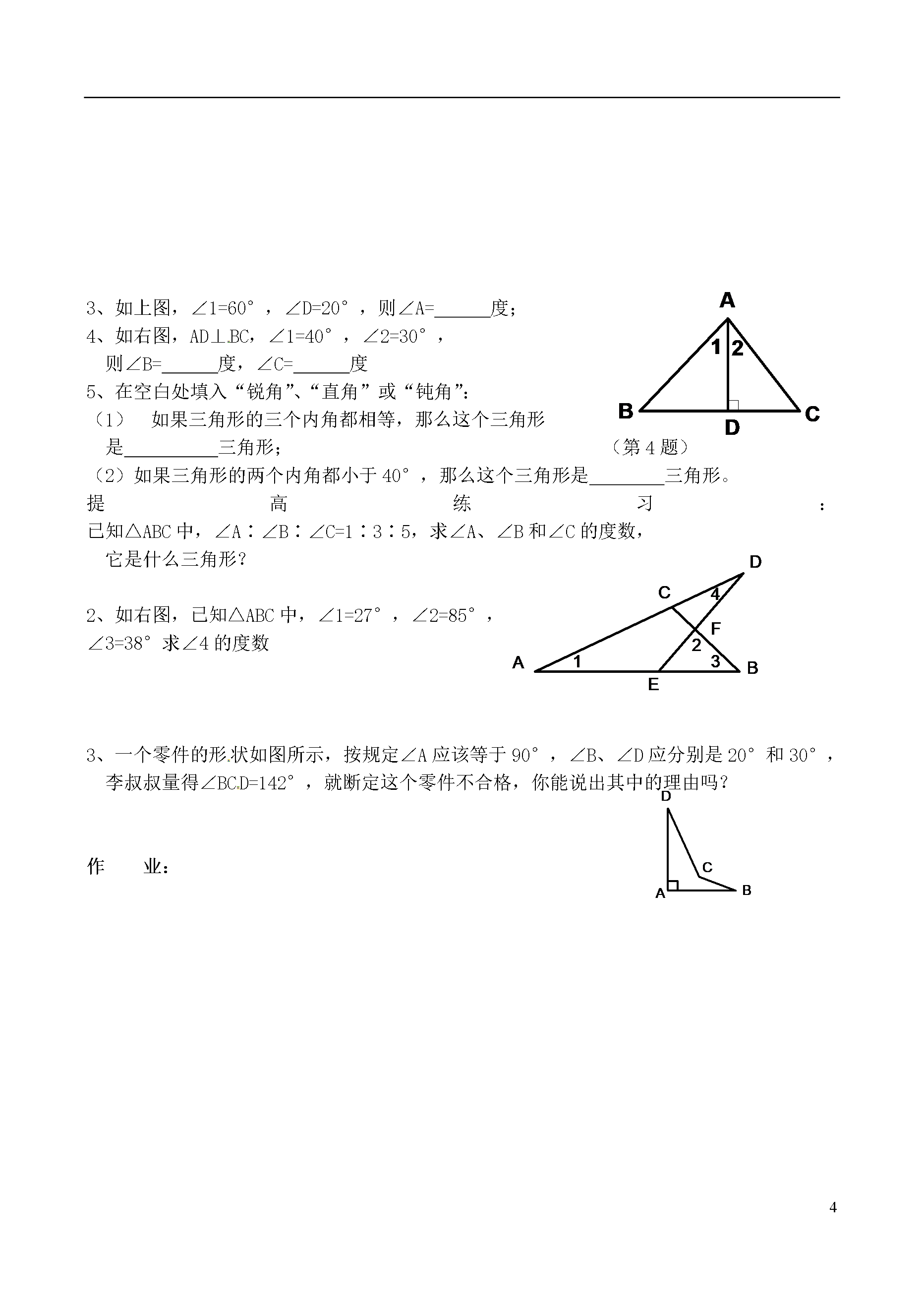
4山东省文登市八年级数学下册5.1认识三角形第二课时教案苏科版教学目标:1、通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力;2、能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”;3、按角将三角形分成三类。教学重难点:三角形内角和定理推理和应用。教学方法:演示、实验法,尝试练习法。教学工具:一副三角板和三个剪好的三角形,课件。活动准备:学生预先剪好两个三角形,一副三角板。教学过程:复习:1、填空:(1)当0°<<90°时,是角;(2)当=°时,是直角;(3

教案-山东-2013_山东省文登市八年级数学下册 5.rar
2认识三角形(3)教案教学目标:1、通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力;2、能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”;3、按角将三角形分成三类。教学重点:1、角平分线的概念2、三角形的中线。教学难点:会角平分线的概念。即判别哪两个角相等。教学方法:演示、实验法,尝试练习法。教学工具:一副三角板和三个剪好的三角形,课件。准备活动:任意一个三角形和锐角三角形、钝角三角形和直角三角形各一个。教学过程:探索练习:任意画一个三角形,设法画出它的

教案-山东-2013_山东省文登市八年级数学下册 5.rar
3山东省文登实验中学八年级数学下册5.1认识三角形第一课时教案苏科版教学目标:1、通过观察、操作、想象、推理、交流等活动,发掌空间观念、推理能力和有条理地表达能力;2、结合具体实例,进一步认识三角形的概念及其基本要素,掌握三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。教学重点:三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。教学难点:灵活运用三角形三边关系解决一些实际问题。教学方法:探索、归纳总结。教学工具:课件准备活动:能从右图中找出4个

教案-山东-2013_山东省文登市高村中学八年级数学下册《5.rar
1山东省文登市高村中学八年级数学下册《5.4数据的波动》教案新人教版教学目标:1、经历数据离散程度的探索过程2、了解刻画数据离散程度的三个量度——极差、标准差和方差,能借助计算器求出相应的数值。教学重点:会计算某些数据的极差、标准差和方差。教学难点:理解数据离散程度与三个“差”之间的关系。教学过程:一、创设情境1、投影课本P170引例。(通过对问题串的解决,使学生直观地估计从甲、乙两厂抽取的20只鸡腿的平均质量,同时让学生初步体会“平均水平”相近时,两者的离散程度未必相同,从而顺理成章地引入刻画数据离散程
