基于广义Sigmoid变换循环模糊函数的时延与多普勒频移联合估计方法.pdf

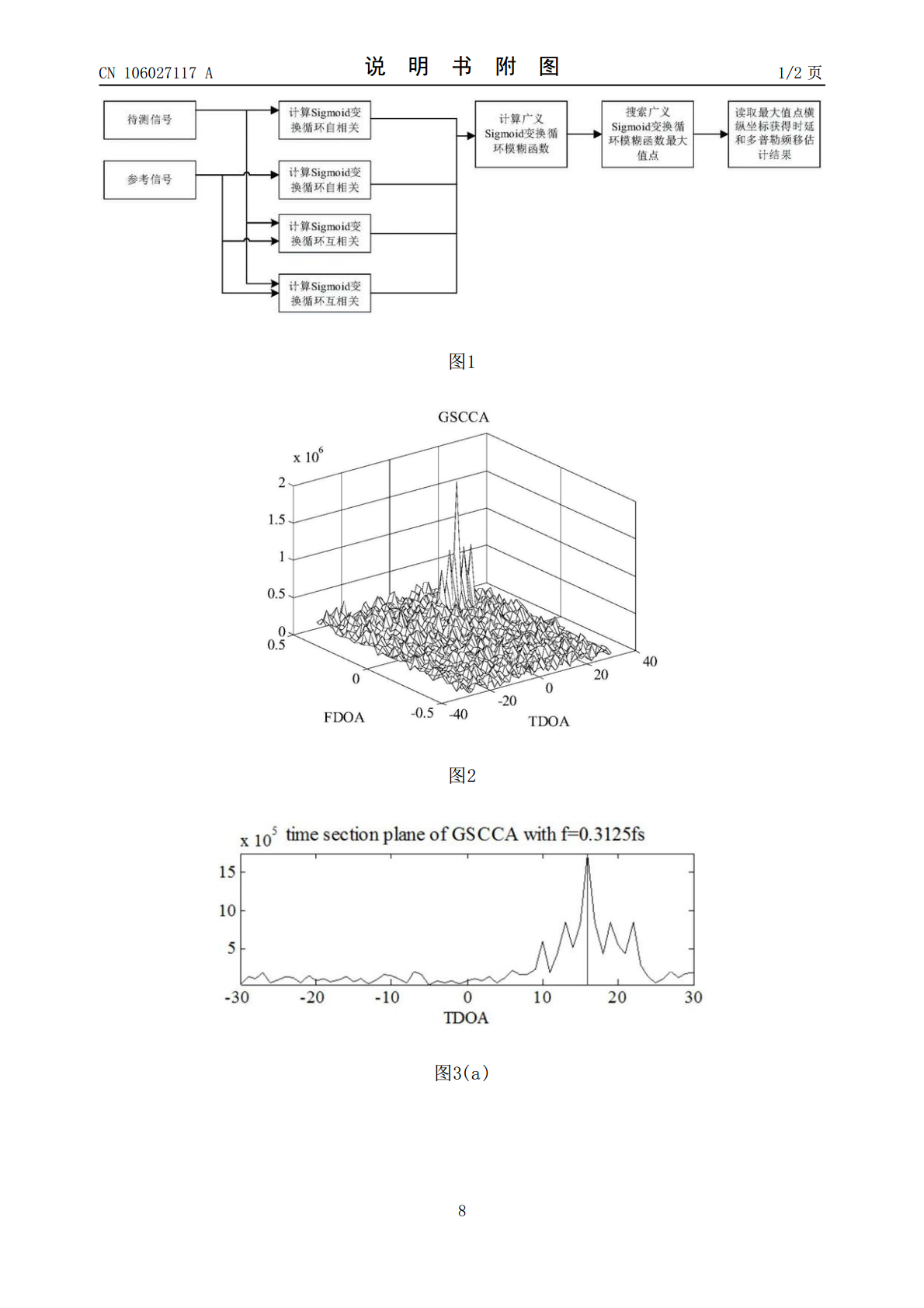
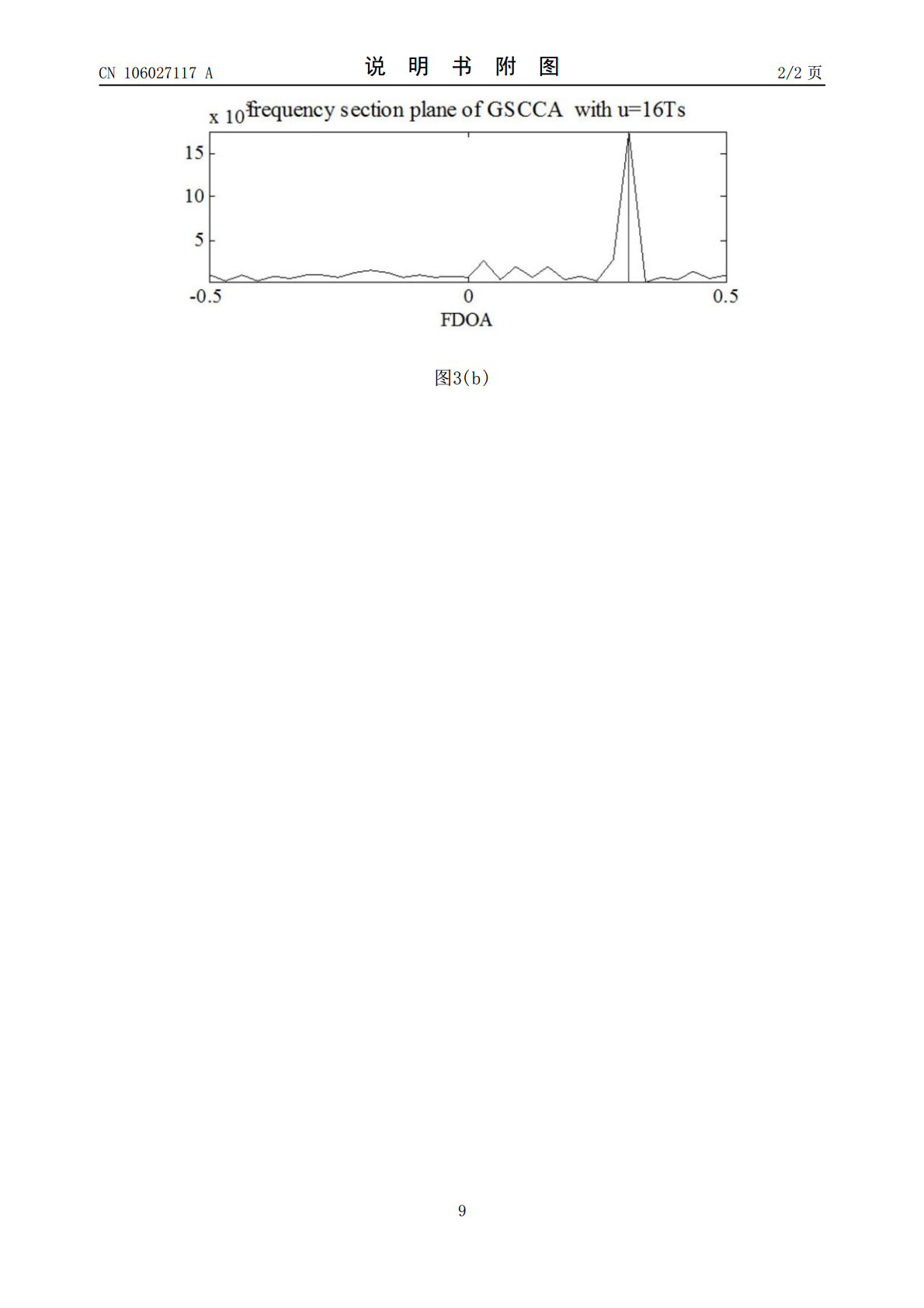
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN106027117A(43)申请公布日2016.10.12(21)申请号201610287197.0(22)申请日2016.05.04(71)申请人大连理工大学地址116024辽宁省大连市甘井子区凌工路2号(72)发明人邱天爽于玲栾声扬王鹏(74)专利代理机构大连理工大学专利中心21200代理人梅洪玉潘迅(51)Int.Cl.H04B1/71(2011.01)H04B1/719(2011.01)权利要求书2页说明书4页附图2页(54)发明名称基于广义Sigmoid变换循环模糊函数的时延与多普勒频移联合估计方法(57)摘要本发明属于循环平稳信号处理技术领域，提供一种基于广义Sigmoid变换循环模糊函数的时延和多普勒频移联合估计方法。其特征是分别求取参考信号的可调Sigmoid变换循环自相关，待测信号的可调Sigmoid变换循环自相关，参考信号与待测信号之间的可调Sigmoid变换循环互相关和待测信号与参考信号之间的可调Sigmoid变换循环互相关，然后求取广义Sigmoid变换循环模糊函数和其绝对值，搜索其绝对值最大值所对应的横纵坐标，获得时延和多普勒频移的估计值。实验证明，本发明能够在脉冲噪声和同频干扰同时存在的情况下对时延和多普勒频移进行准确估计，且具有较强的抗脉冲噪声能力。CN106027117ACN106027117A权利要求书1/2页1.一种基于广义Sigmoid变换循环模糊函数的时延与多普勒频移联合估计的方法，其特征在于，包括以下步骤：第一步，计算广义Sigmoid变换循环模糊函数1.1)利用可调Sigmoid变换循环自相关公式计算参考信号x(t)在时间区间[-T/2,T/2]上的可调Sigmoid变换循环自相关如公式(1)所示：由公式(2)估计得到采集数据为有限长度时的可调Sigmoid变换循环自相关其中，ε表示循环频率，由s(t)的循环频率确定；τ表示时延；x(t)为接收到的参考信号，x(t)＝s(t)+w1(t)+sI(t)；w1(t)为加性噪声，设加性噪声为服从位置参数a＝0、对称参数β＝0的Alpha稳定分布噪声，若加性噪声为高斯分布或无干扰信号，不影响后续的估计步骤及估计结果；s(t)为具有循环平稳特性的发射信号；sI(t)为干扰信号，sI(t)和s(t)的载频相同，波特率不同；加性噪声项w1(t)和干扰项sI(t)为脉冲噪声与同频干扰并存下的信号模型；Sigmoid[x(t)]表示如公式(3)所示的对x(t)进行可调Sigmoid变换；1.2)利用可调Sigmoid变换循环自相关公式计算待测信号y(t)在时间区间[-T/2,T/2]上的可调Sigmoid变换循环自相关如公式(4)所示：采集数据为有限长度时的可调Sigmoid变换循环自相关可由公式(5)估计得到；其中，为待测信号；D为待估计的时间延迟；fd为待估计的多普勒频移；w2(t)为加性噪声；1.3)利用可调Sigmoid循环互相关公式计算参考信号与待测信号之间的可调Sigmoid循环互相关采集数据为有限长度时的估计公式为：2CN106027117A权利要求书2/2页1.4)利用可调Sigmoid循环互相关公式计算待测信号与参考信号之间的可调Sigmoid循环互相关采集数据为有限长度时的估计公式为1.5)根据广义Sigmoid循环模糊函数公式，计算得到广义Sigmoid循环模糊函数u和f分别代表时延和多普勒频移；第二步，参数估计计算公式(10)广义Sigmoid循环模糊函数的绝对值；绝对值最大值的一组时延值u和多普勒频移f，为待测信号的估计值如公式(11)所示。3CN106027117A说明书1/4页基于广义Sigmoid变换循环模糊函数的时延与多普勒频移联合估计方法技术领域[0001]本发明属于循环平稳信号处理技术领域，涉及到时延和多普勒频移联合估计的方法，特别涉及一种使用广义Sigmoid变换循环模糊函数的时延与多普勒频移联合估计的方法。背景技术[0002]大多数通信、雷达信号都具有循环平稳特性，利用这一特性可以有效去除同频带干扰信号的影响。循环模糊函数就是应用了循环平稳理论的一个经典方法，用于同频干扰下的时延和多普勒频移联合估计具有很好的效果。但是该方法是基于噪声服从高斯分布的假设下的，当噪声中包含脉冲特性时算法性能将严重退化或失效。[0003]基于分数低阶统计量理论的分数低阶循环模糊函数，可以同时在脉冲噪声和同频干扰下工作，但也有其固有的缺点：分数低阶的阶数需要噪声的先验知识，否则阶数的不当选择会影响方法的估计效果，另外，分数低阶统计量在脉冲性较强时，对脉冲噪声抑制能力不足，从而导致估计误差增大。故本发明提出一种可调Sigmoid变换循环相关，在可调Sigmoi