
初中常考几何模型及构造方法.doc

映雁****魔王




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

初中常考几何模型及构造方法.docx
初中常考几何模型及构造方法对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等

初中常考几何模型及构造方法.docx
初中常考几何模型及构造方法对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等

初中常考几何模型及构造方法.doc
初中常考几何模型及构造方法初中几何是学生开始较系统地学习几何知识的重要科目因此初中几何教学可以说是学生的几何学的启蒙教学学好初中几何对学生今后学习更高层次的几何有很好的奠基作用。平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线形成对称全等。两边进行边或者角的等量代换产生联系。垂直也可以做为轴进行对称全等。对称半角模型说明:上图依次是45°、30&
初中数学常用几何模型及构造方法大全.pdf
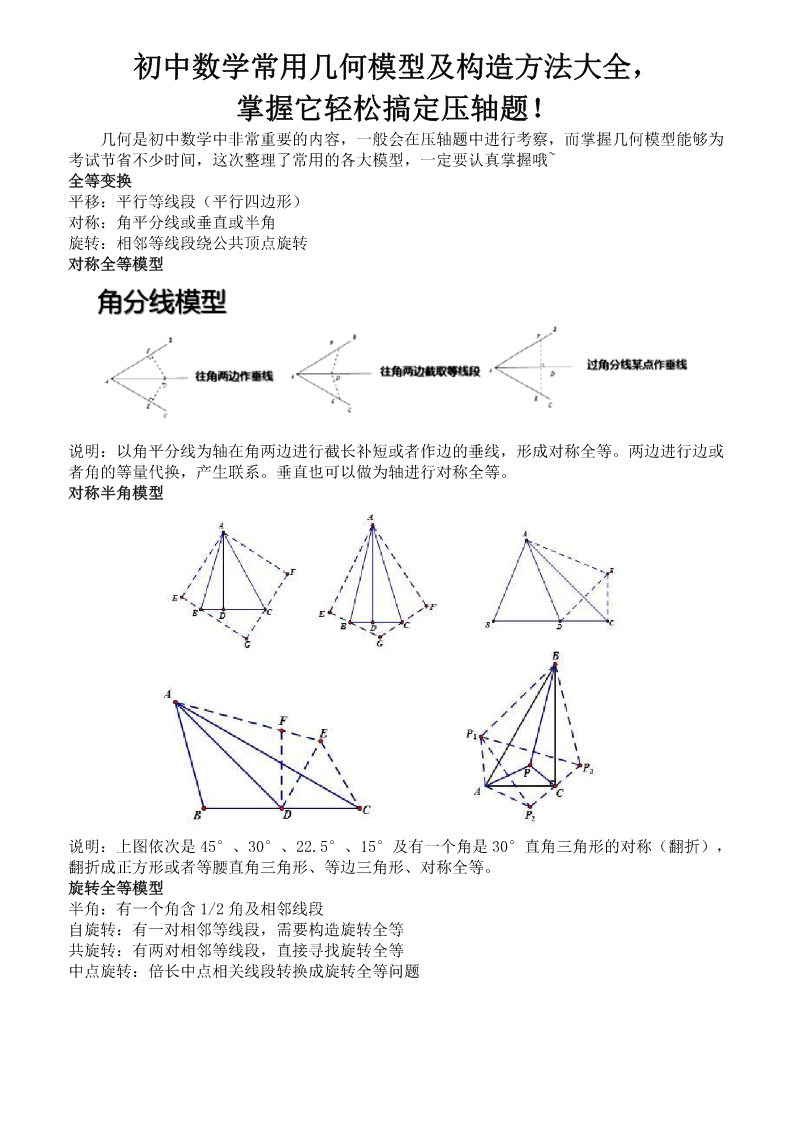
TheshortestwaytodomanythingsistoonlyonethingatatimeandAllthingsintheirbeingaregoodforsomethingandSufferingisthemostpowerfulteacheroflife初中数学常用几何模型及构造方法大全,掌握它轻松搞定压轴题!几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对

初中数学常用几何模型及构造方法大全.doc
初中数学常用几何模型及构造方法大全,掌握它轻松搞定压轴题!几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一
