
(中位线定理).docx

觅松****哥哥









亲,该文档总共14页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

(中位线定理).docx
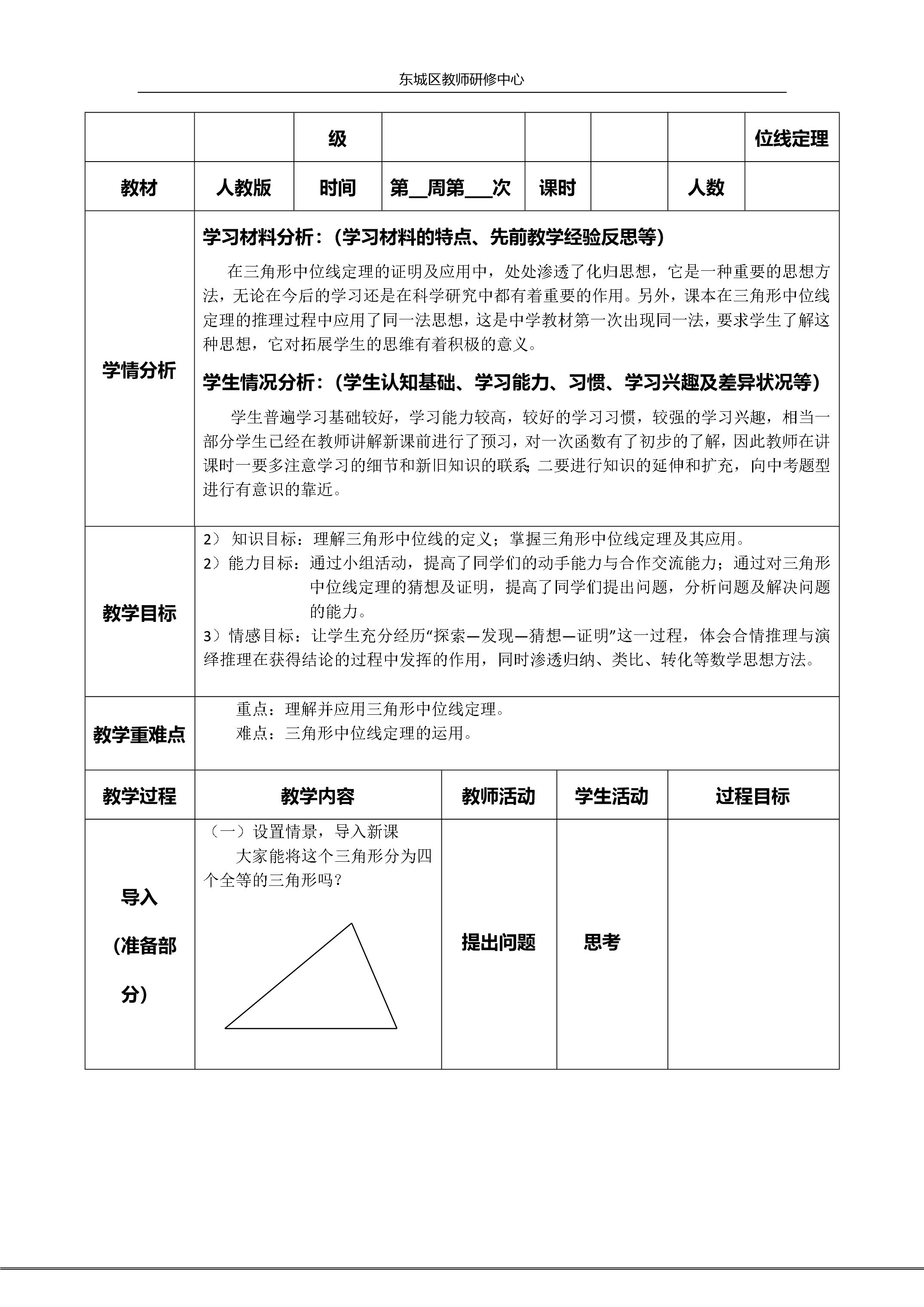
东城区教师研修中心教材单元分析教材人教版单元内容三角形中位线定理课本页码第页至第页年级初二教师本单元教材的作用与地位:三角形中位线是三角形中重要的线段,三角形中位线定理是一个重要性质定理,它是前面已学过的平行线、全等三角形、平行四边形等知识内容的应用和深化,对进一步学习非常有用,尤其是在判定两直线平行和论证线段倍分关系时常常用到。在三角形中位线定理的证明及应用中,处处渗透了化归思想,它是一种重要的思想方法,无论在今后的学习还是在科学研究中都有着重要的作用,它对拓展学生的思维有着积极的意义。2.教学指导思想

(中位线定理).docx
东城区教师研修中心教材单元分析教材人教版单元内容三角形中位线定理课本页码第页至第页年级初二教师本单元教材的作用与地位:三角形中位线是三角形中重要的线段,三角形中位线定理是一个重要性质定理,它是前面已学过的平行线、全等三角形、平行四边形等知识内容的应用和深化,对进一步学习非常有用,尤其是在判定两直线平行和论证线段倍分关系时常常用到。在三角形中位线定理的证明及应用中,处处渗透了化归思想,它是一种重要的思想方法,无论在今后的学习还是在科学研究中都有着重要的作用,它对拓展学生的思维有着积极的意义。2.教学指导思想

中位线定理.ppt
A三角形中位线定理定义:连接三角形两边中点的线段叫做三角形的中位线。测量猜想E三角形的中位线定理:抢答题例题D是△ABC内一点,E、F、G、H分别是AB、AC、DC、DB的中点,求证:四边形EFGH是平行四边形变式求证:如图,顺次连接任意四边形各边的中点,所得的四边形是平行四边形。1.已知:如图,DE是⊿ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.勇攀高峰方法点拨:应用时,要同时出现三角形和中位线①若有两中点连线而无三角形:要连接第三边,构成一个三角形②若有三角形而

中位线定理.pptx
三角形的中位线如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。温馨提示(1)相同之处——都和边的中点有关;(2)不同之处:三角形中位线的两个端点都是边的中点;三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。友情提醒:猜一猜:已知:如图:在△ABC中,D是AB的中点,E是AC的中点。求证:三角形中位线定理A如图所示,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列

中位线定理.ppt
三角形的中位线如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。温馨提示(1)相同之处——都和边的中点有关;(2)不同之处:三角形中位线的两个端点都是边的中点;三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。友情提醒:猜一猜:已知:如图:在△ABC中,D是AB的中点,E是AC的中点。求证:三角形中位线定理A如图所示,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列
