预览加载中，请您耐心等待几秒...

二次根式复习课件最优.pptx

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

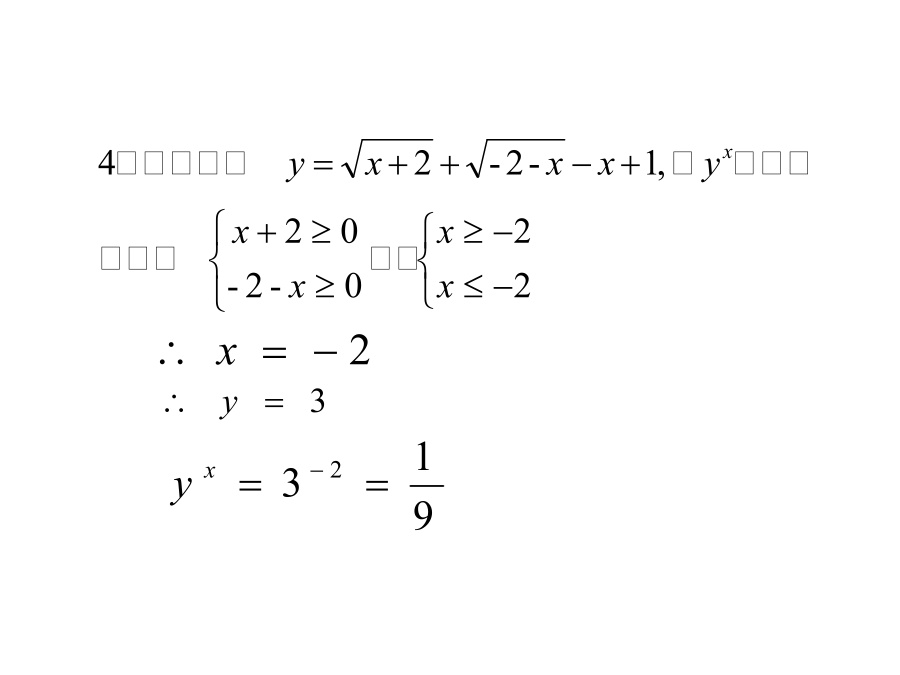
亲，该文档总共24页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

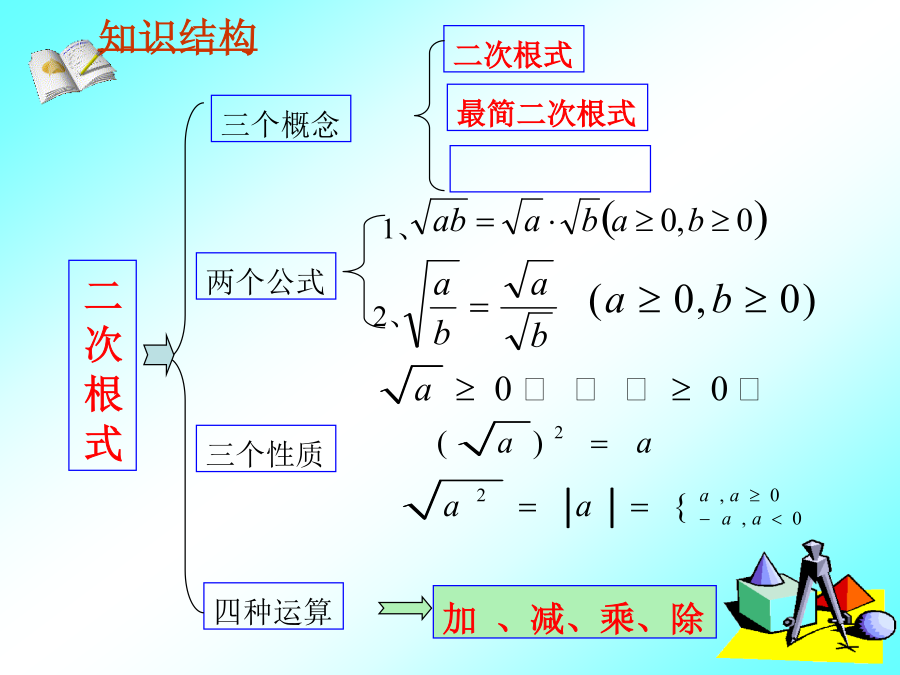
二十二章二次根式复习二次根式二次根式的乘除：二次根式的概念例．下列各式中那些是二次根式？ 那些不是？为什么？二次根式的性质题型1:确定二次根式中被开方数所含字母的取值范围.5、已知x、y是实数，且 求3x+4y的值。题型2:二次根式的非负性的应用.题型3最简二次根式：题型3：利用2．（１） （２）当时， （３）， 则Ｘ的取值范围是＿＿＿ （４）若， 则Ｘ的取值范围是＿＿＿3、二次根式的混合运算试一试:一个台阶如图，阶梯每一层高15cm，宽25cm，长60cm.一只蚂蚁从A点爬到B点最短路程是多少？（1）判断下列各式是否成立？你认为成立的，请在括号里 打“√”，不成立的，请在括号里打“×” 拓展1若a为底,b为腰,此时底边上的高为变式应用你有收获吗? 复习题22 第11题