
量子统计南大说课讲解.ppt

王子****青蛙










亲,该文档总共51页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

量子统计南大说课讲解.ppt
第八章、玻色统计和费米统计我们引进巨配分函数:总能量:对于一个孤立的系统,粒子数目的变化为零,有:根据ln的定义,以及最可几分布给出的参数间的关系,可以得到玻尔兹曼关系式:,其中我们已经取积分常数为零。对于一个开放的系统,粒子数目的变化不为零,有:对于遵从玻色、费米分布的系统,只要求出了系统的巨配分函数的对数ln,就可以求出系统的平均粒子数、内能、物态方程、熵等,从而确定系统的所有的平衡性质。ln是以,,y(对应简单系统,即:T,V,)为自然变量的特征函数。热力学中知道,这种系统的特征函数是

南河中学王雅琴说课讲解.ppt
正比例函数问题与探究写出下列问题中的函数关系式观察与发现应用新知正比例函数的图象思考:(1)y=2x的图象是什么?它经过那些象限?(2)从左至右,随着x的增大,y的值如何变化?图象的变化趋势如何?试一试请你画出观察比较两个函数的相同点与不同点.练一练直线y=kx应用新知1、已知y与x-1成正比例,且x=-3时,y=82、已知某种小汽车的耗油量是每100km耗油15升.所使用的90#汽油今日涨价到5元/升.(1)写出汽车行驶途中所耗油费y(元)与行程x(km)之间的函数关系式;(2)在平面直角坐标系内描出大
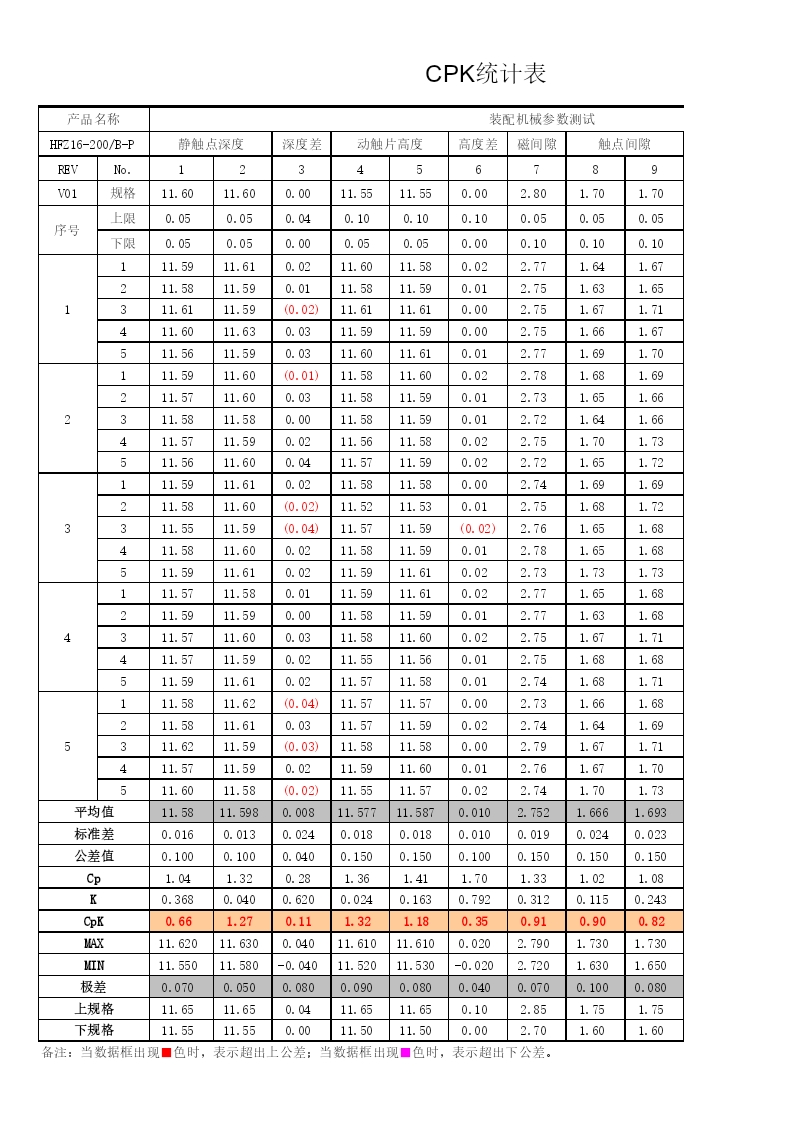
CPK统计表说课讲解.xls
CPK统计表产品名称装配机械参数测试HFZ16-200/B-P静触点深度深度差动触片高度高度差磁间隙触点间隙触点间隙差超行程触点压力返回力REVNo.12345678910111213V01规格11.6011.600.0011.5511.550.002.801.701.700.001.105.6022.00序号上限0.050.050.040.100.100.100.050.050.050.080.100.602.00下限0.050.050.000.050.050.000.100.100.100.000.1

社会统计学作业说课讲解.doc
社会统计学作业精品资料精品资料仅供学习与交流,如有侵权请联系网站删除谢谢仅供学习与交流,如有侵权请联系网站删除谢谢精品资料仅供学习与交流,如有侵权请联系网站删除谢谢2015-2016学年第1学期社会统计学课程论文任课教师:林诚彦名称:关于校园食品安全问题调查方案班级:2014级公共管理16班学号姓名评分组长201430841601敖骏明组员201430841605段映杰组员201430841622欧阳诗论组员201430790323周梓一组员201431140

质量统计用图法说课讲解.ppt
质量管理常用统计方法Statisticalmethodsinqualitymanagement1、了解数据、总体、样本的含义及随机抽样的一般方法;2、掌握排列图、因果分析图的作图方法和应用;3、掌握分层法、统计图表法的应用;4、了解直方图的原理、作用、作图方法及应用;A.V.Feigenbaum的观点:2000.6.12000.6.12000.6.12000.6.12000.6.12000.6.12000.6.12000.6.12000.6.12000.6.12000.6.12000.6.12000.6.
