带电粒子在有界匀强磁场中的圆周运动.pptx

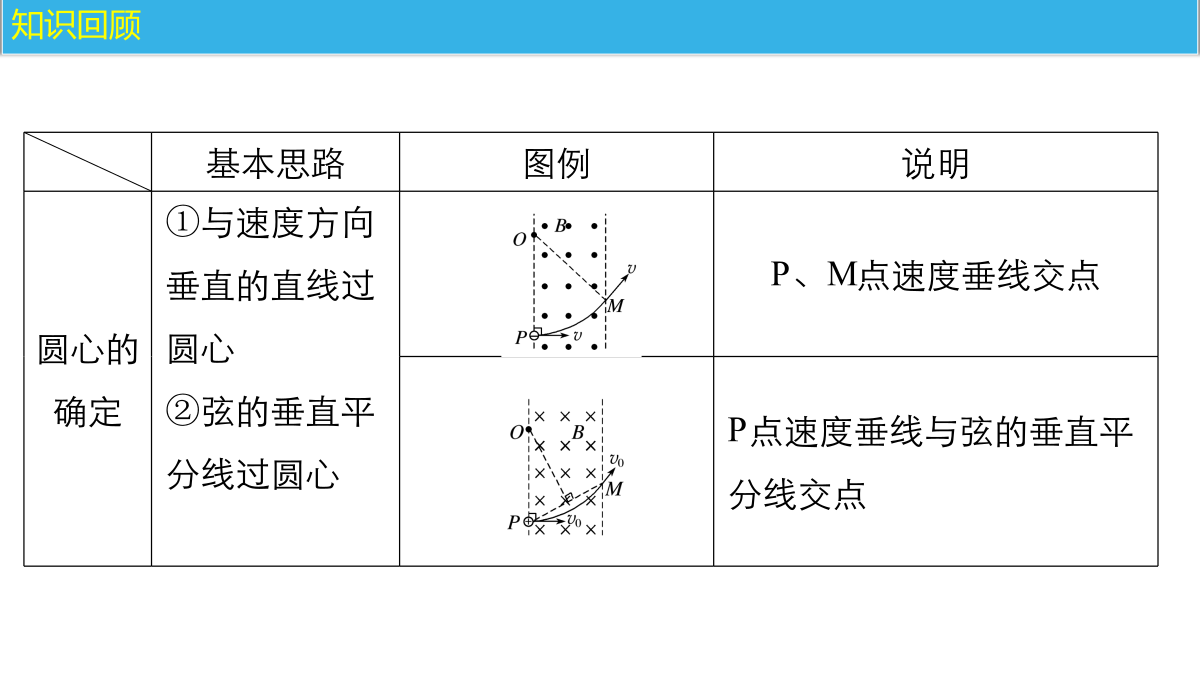
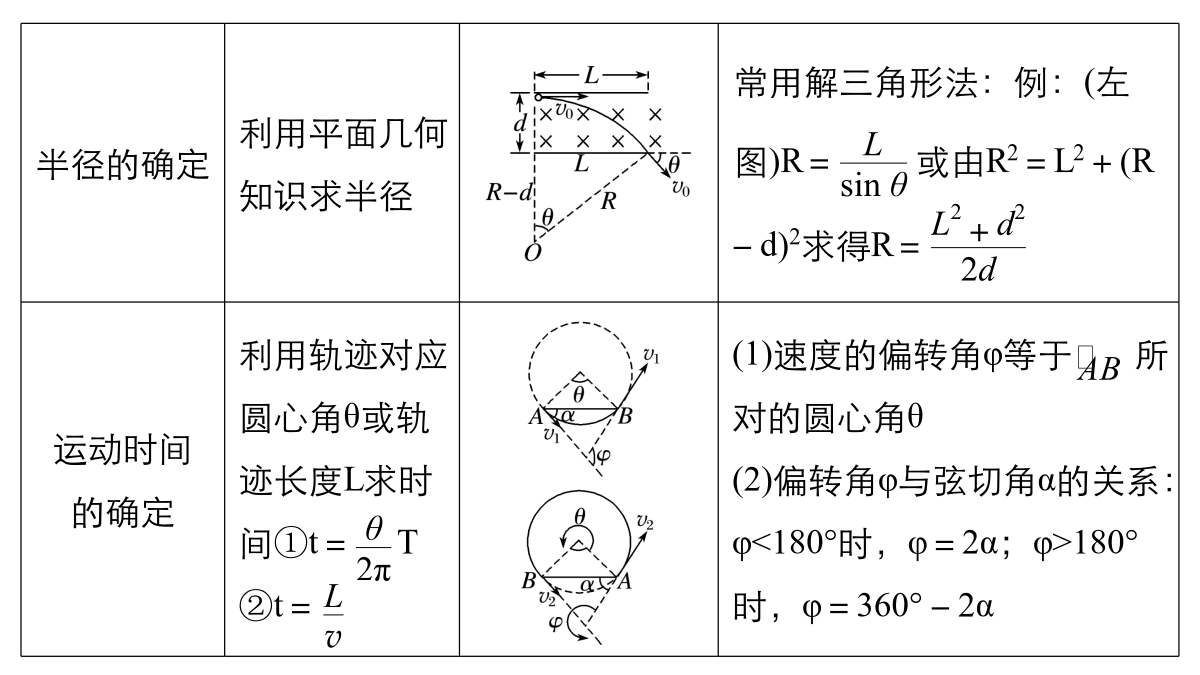
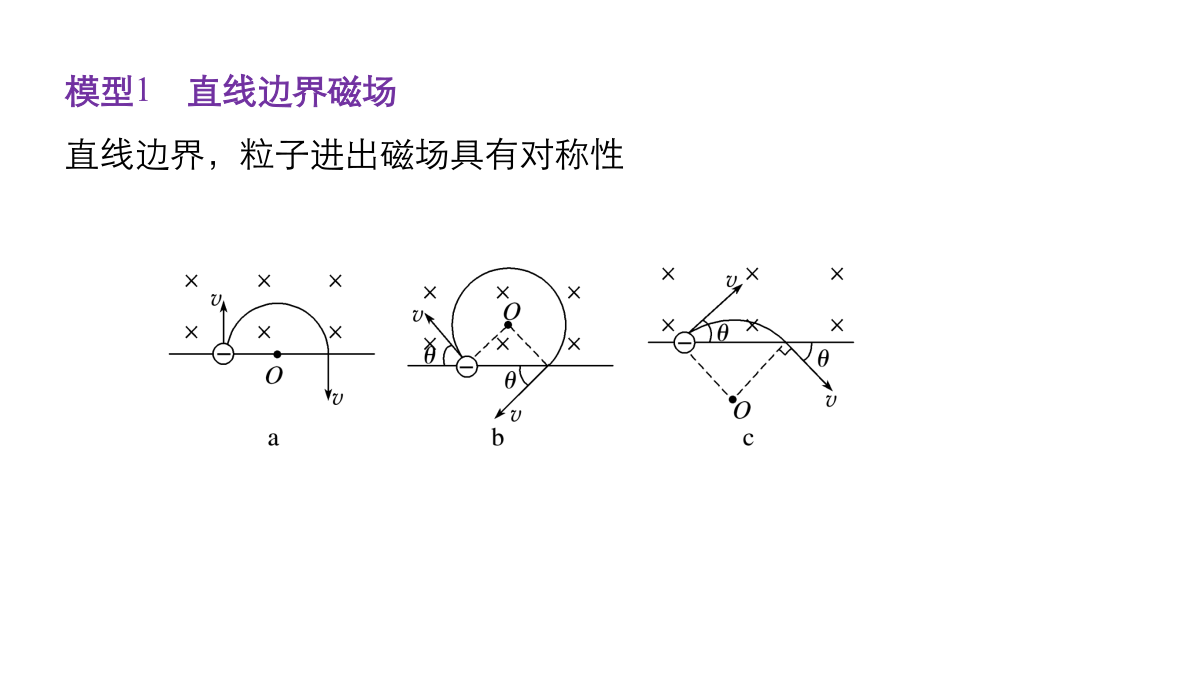
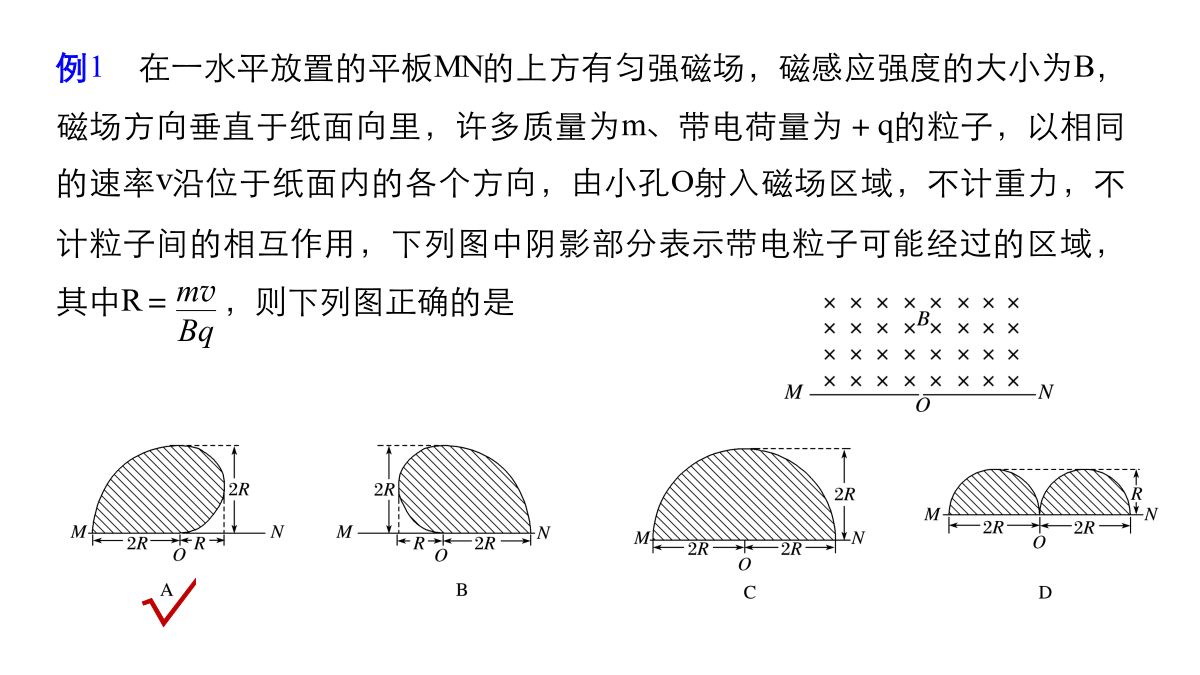
知识回顾半径的确定模型1直线边界磁场
直线边界，粒子进出磁场具有对称性例1在一水平放置的平板MN的上方有匀强磁场，磁感应强度的大小为B，磁场方向垂直于纸面向里，许多质量为m、带电荷量为＋q的粒子，以相同的速率v沿位于纸面内的各个方向，由小孔O射入磁场区域，不计重力，不计粒子间的相互作用，下列图中阴影部分表示带电粒子可能经过的区域，其中R＝，则下列图正确的是模型2平行边界磁场
平行边界存在临界条件例2如图甲所示的直角坐标系内，在x0(x0>0)处有一垂直x轴放置的挡板.在y轴与挡板之间的区域内存在一个与xOy平面垂直且指向纸内的匀强磁场(图中未画出)，磁感应强度B＝0.2T.位于坐标原点O处的粒子源向xOy平面内发射出大量同种带正电的粒子，所有粒子的初速度大小均为v0＝1.0×106m/s，方向与x轴正方向的夹角为θ，且0≤θ≤90°，该粒
子的比荷为＝1.0×108C/kg，不计粒子
所受重力和粒子间的相互作用，粒子打
到挡板上后均被挡板吸收.
(1)求粒子在磁场中运动的轨道半径R；(2)如图乙所示，为使沿初速度方向与x轴正方向的夹角θ＝30°射出的粒子不打到挡板上，则x0必须满足什么条件？该粒子在磁场中运动的时间是多少？解析如图甲所示，设粒子的运动轨迹恰好与挡板相切，
由几何关系得：x0＝R＋Rsinθ
解得：x0＝7.5×10－2m
为使该粒子不打到挡板上：x0≥7.5×10－2m(3)若x0＝5.0×10－2m，求粒子打在挡板上的范围(用y坐标表示)，并用“”图样在图丙中画出粒子在磁场中所能到达的区域.解析若x0＝5.0×10－2m，则x0＝R
当粒子沿着－y方向入射时，将打在挡板上的A点，其纵坐标：yA＝－R＝－5.0×10－2m
当粒子沿着＋x方向入射时，粒子的运动轨迹恰好与挡板
相切于B点，其纵坐标：yB＝R＝5.0×10－2m
则粒子打在挡板上的范围为：－5.0×10－2m≤y<5.0×10－2m.
粒子在磁场中所能到达的区域如图乙所示.模型3圆形边界磁场
沿径向射入圆形磁场必沿径向射出，运动具有对称性例3.如图所示，在半径为R＝的圆形区域内有垂直纸面向里的匀强磁场，磁感应强度为B，圆形区域右侧有一竖直感光板，从圆弧顶点P以速率v0的带正电粒子平行于纸面进入磁场，已知粒子的质量为m，电荷量为q，粒子重力不计.
(1)若粒子对准圆心射入，求它在磁场中运动的时间；解析设带电粒子进入磁场中做匀速圆周运动的轨道半径为r，
由牛顿第二定律得Bqv0＝m
r＝R
带电粒子在磁场中的运动轨迹为四分之一圆周，轨迹对应的圆心角为，如图甲所示，(2)若粒子对准圆心射入，且速率为v0，求它打到感光
板上时速度的垂直分量；(3)若粒子以速度v0从P点以任意角入射，试证明它离开磁场
后均垂直打在感光板上.随堂测试1.如图所示，虚线上方存在匀强磁场，磁感应强度为B；一群电子以不同速率v从边界上的P点以相同的方向射入磁场.其中某一速率为v0的电子从Q点射出.已知电子入射方向与边界夹角为θ，则由以上条件可判断

A.该匀强磁场的方向垂直纸面向里
B.所有电子在磁场中的轨迹相同
C.速率大于v0的电子在磁场中运动时间长
D.所有电子的速度方向都改变了2θ2、如图所示，虚线所示的圆形区域内存在一垂直于纸面的匀强磁场，P为磁场边界上的一点，大量相同的带电粒子以相同的速率经过P点，在纸面内沿不同的方向射入磁场，若粒子射入速率为v1，这些粒子在磁场边界的出射点分布在六分之一圆周上；若粒子射入速率为v2，相应的出射点分布在三分之一圆周上，不计重力及带电粒子之间的相互作用，则v2∶v1为解析当粒子在磁场中运动半个圆周时，打到圆形磁场边界的位置距P点最远，则当粒子射入的速率为v1，轨迹如图甲所示，设圆形磁场半径为R，由几何知识可知，粒子运动的轨道半径为r1＝Rcos60°＝R；本课结束谢谢