对数函数图像及性质教学.ppt

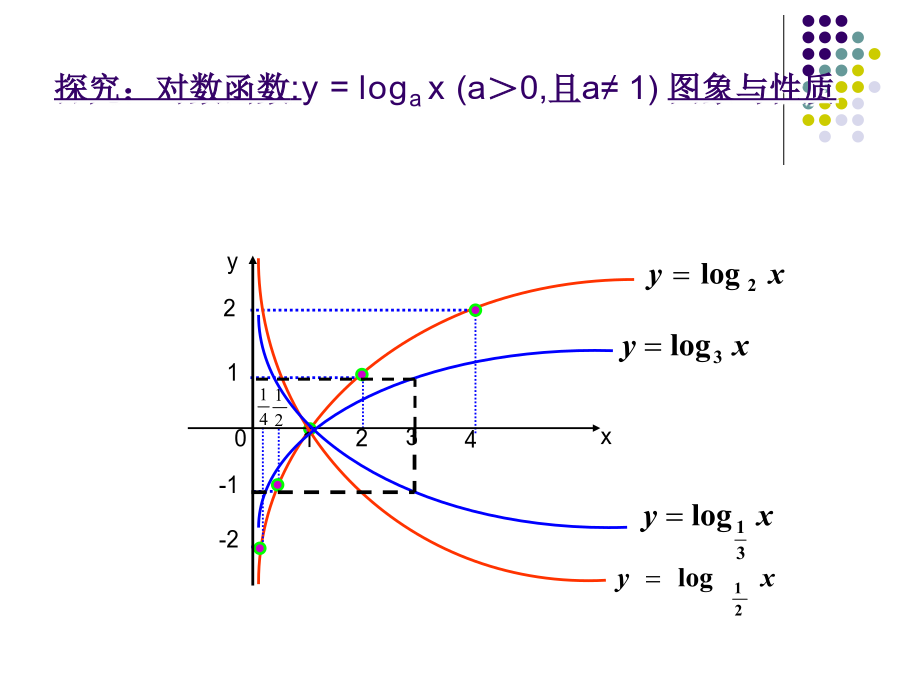
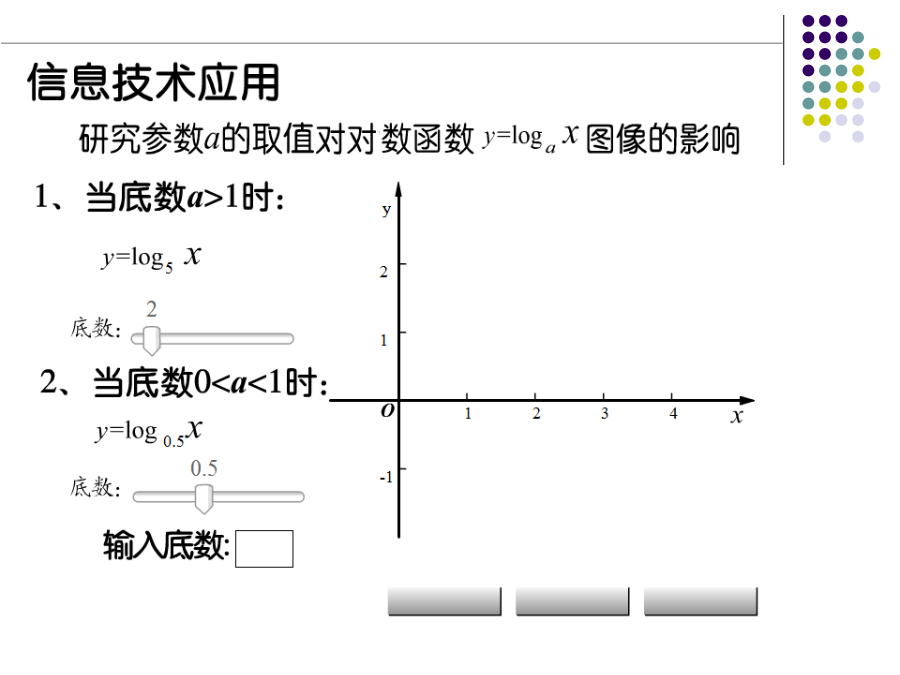
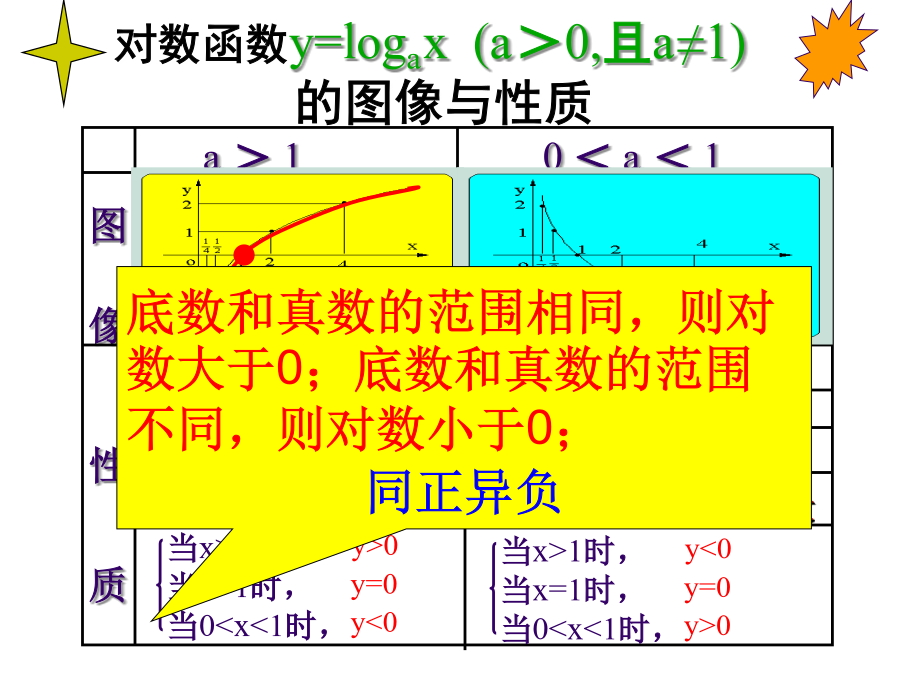
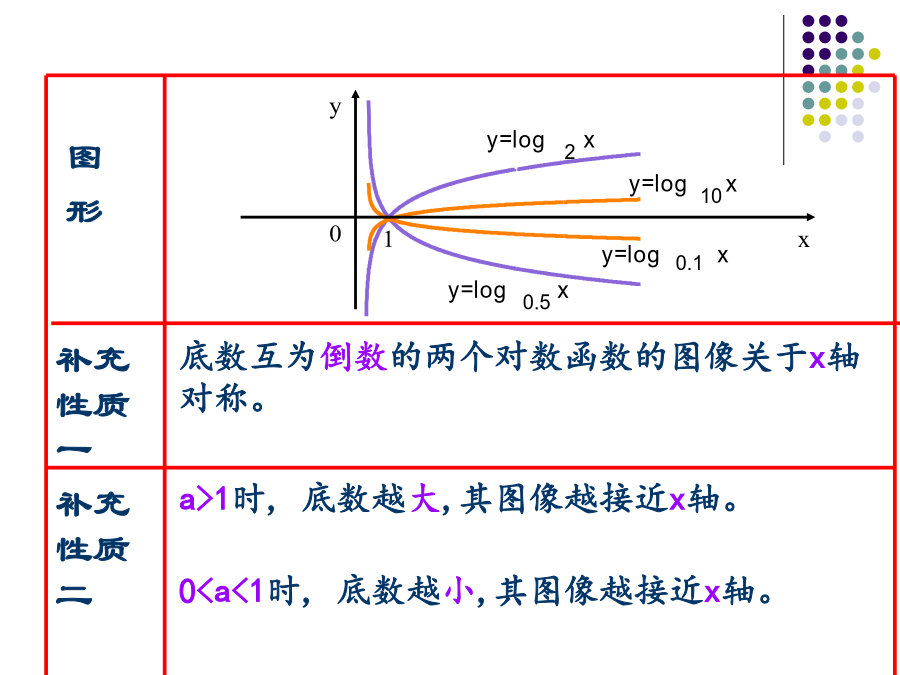
5.3对数函数的图像和性质1.对数函数的概念：
我们把叫作对数函数，
其中定义域是,值域是R,叫作对数函数的
底数.用描点法画出对数函数

的图像。探究：对数函数:y=logax(a＞0,且a≠1)图象与性质二、对数函数的图象和性质图像性质补充性质二比较下列各组中，两个值的大小：
（1）log25.3与log24.7（2）log0.27与log0.29比较下列各组中，两个值的大小：
（1）log25.3与log24.7（2）log0.27与log0.29注意：若底数不确定，那就要对底数进行分类讨论
即0<a<1和a>1比较下列各组中两个值的大小:
⑴log67,log76;⑵log3π,log20.8（3）【变式练习】㈠若底数为同一常数,则可由对数函数的单调性直接进行判断.
㈡若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.
㈢若底数、真数都不相同,则常借助1、0、－1等中间量进行比较。
（四）若真同底不同，利用中间数法、图像法或倒数公式法。解：从图（1）上可以看出，点P（a,b）与点Q（b,
a）关于直线y=x对称.函数y=log2x与函数y=2x互为反函数，对应于函数y=log2x图像上的任意一点P（a,
b），P点关于直线y=x的对称点Q(b,a)总在函数y=2x图像上，所以，函数y=log2x的图像与函数y=2x的图像关于直线y=x对称（如图（2））.例4人们早就发现了放射性物质的衰减现象.在考古工作中，常用14C的含量来确定有机物的年代，已知放射性物质的衰减服从指数规律：
C（t）=C0e–rt，
其中t表示衰减的时间，C0表示放射性物质的原始质量，C（t）表示经衰减了t年后剩余的质量.为计算衰减的年代，通常给出该物质质量衰减一半的时间，称其为该物质的半衰期，14C的半衰期大约是5730年，由此可确定系数r.人们又知道，放射性物质的衰减速度是与其质量成正比的.1950年在巴比伦发现一根刻有Hammurbi王朝字样的木炭，当时测定，其14C分子的衰减速度为4.09个/(g·min),而新砍伐烧成的木炭中14C的衰减速度为6.68个/(g·min),请估算出Hammurbi王朝所在年代.解:因为14C的半衰期大约是5730年，所以建立方程
=e-5730r
解得r=0.000121,由此可知14C的衰减规律服从指数型函数C（t）=C0e-0.000121t
设发现Hammurbi王朝木炭时（公元1950年）,该木炭已衰减了t0年，因为放射性物质的衰减速度是与其质量成正比的，所以
于是=
两边取自然对数，得
-0.000121t0=㏑4.09-㏑6.68,
解得t0≈4054（年）
即Hammurbi王朝大约存在于公元前2100年.1.函数的定义域为__________.1.对数函数的图像和性质.
2.函数y=f(x)与它的反函数的图像关于直线y=x对称.