
大学线性代数期末复习串讲.ppt

YY****。。

1/10

2/10

3/10

4/10

5/10
6/10
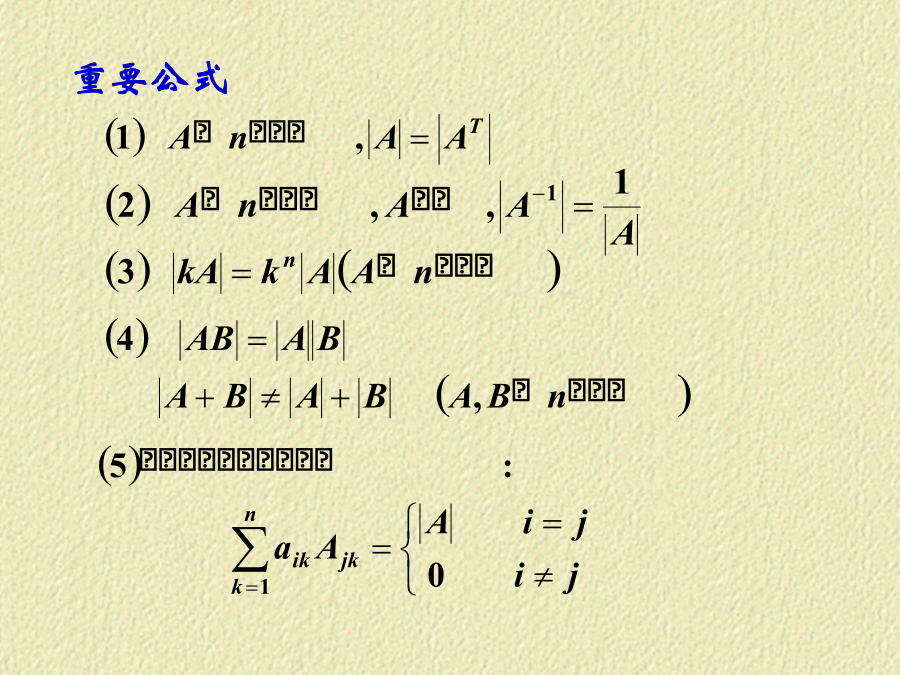
7/10

8/10

9/10

10/10
亲,该文档总共59页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

大学线性代数期末复习串讲.ppt
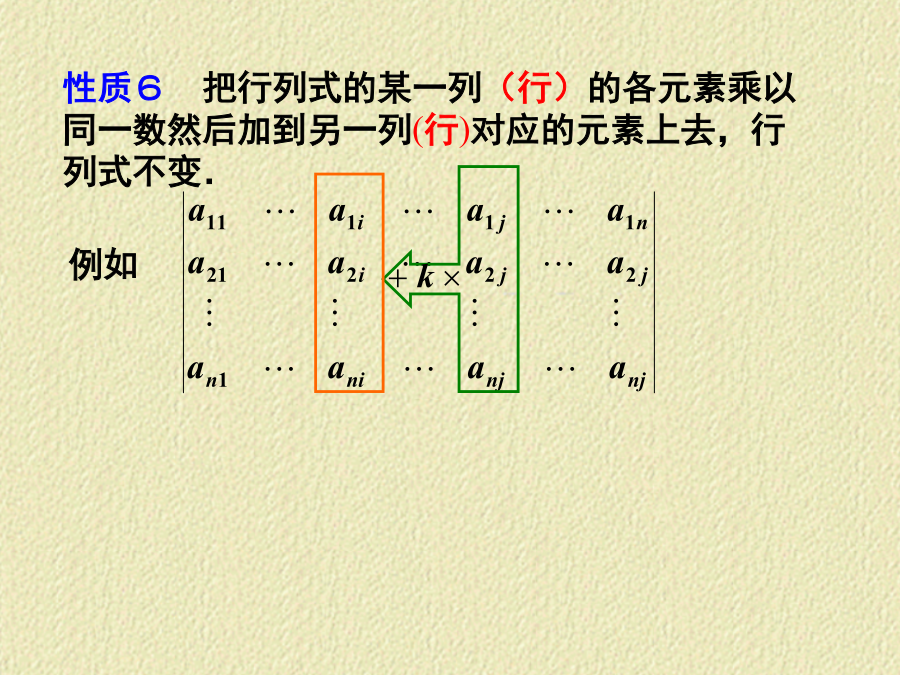
线性代数串讲行列式的性质性质2:性质3:性质5若行列式的某一列的元素都是两数之和.性质6把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变.重要公式行列式计算(利用性质)矩阵结论:3.特殊矩阵:单位矩阵,数量矩阵,对角矩阵,上(下)三角矩阵4.重要矩阵及运算性质满足运算规律:对称矩阵:可逆矩阵的逆矩阵奇异矩阵例正交矩阵及其性质5.矩阵的初等变换及性质向量结论:1.m个n维向量必线性相关.(m>n)定理(1)若向量组A:线性相关,则向量组B:也线性相关.反之,若向量组B线

线性代数(经管类)串讲.pptx
《线性代数》(经管类)串讲第二页共二十页。第三页共二十页。第四页共二十页。第五页共二十页。第六页共二十页。第七页共二十页。第八页共二十页。第九页共二十页。第十页共二十页。第十一页共二十页。第十二页共二十页。第十三页共二十页。第十四页共二十页。第十五页共二十页。第十六页共二十页。第十七页共二十页。第十八页共二十页。查看《线性代数(经管类)》串讲资料全部内容>>请进入华夏大地教育网串讲班、冲刺班、强化班、全程班祝大家考试成功!内容总结

线性代数》经管类串讲.pptx
《线性代数》(经管类)串讲

《线性代数》(经管类)串讲.ppt
《线性代数》(经管类)串讲

线性代数(经管类)串讲.pptx
