多样本的非参数检验.ppt

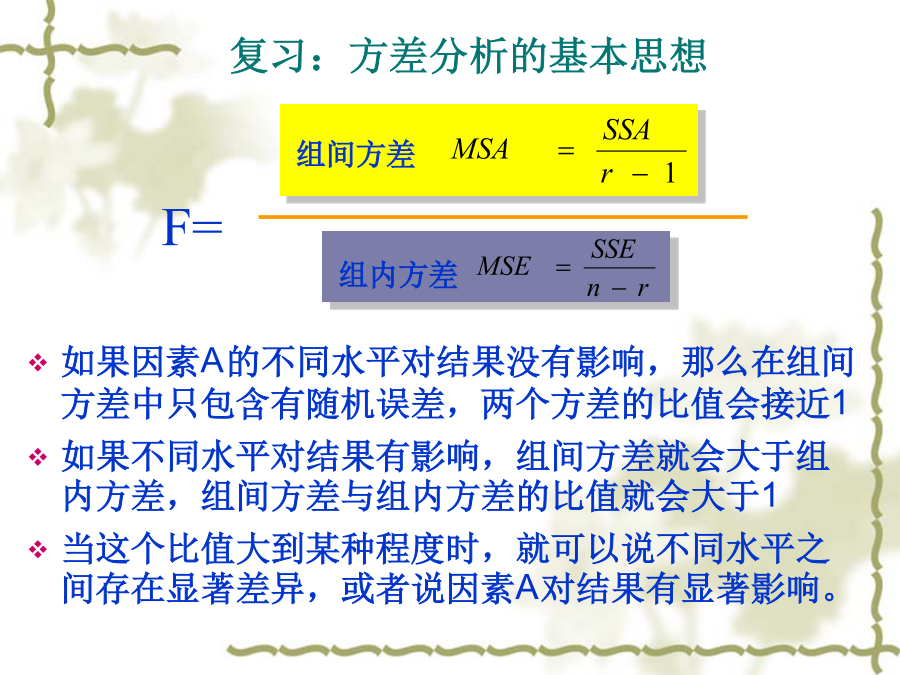
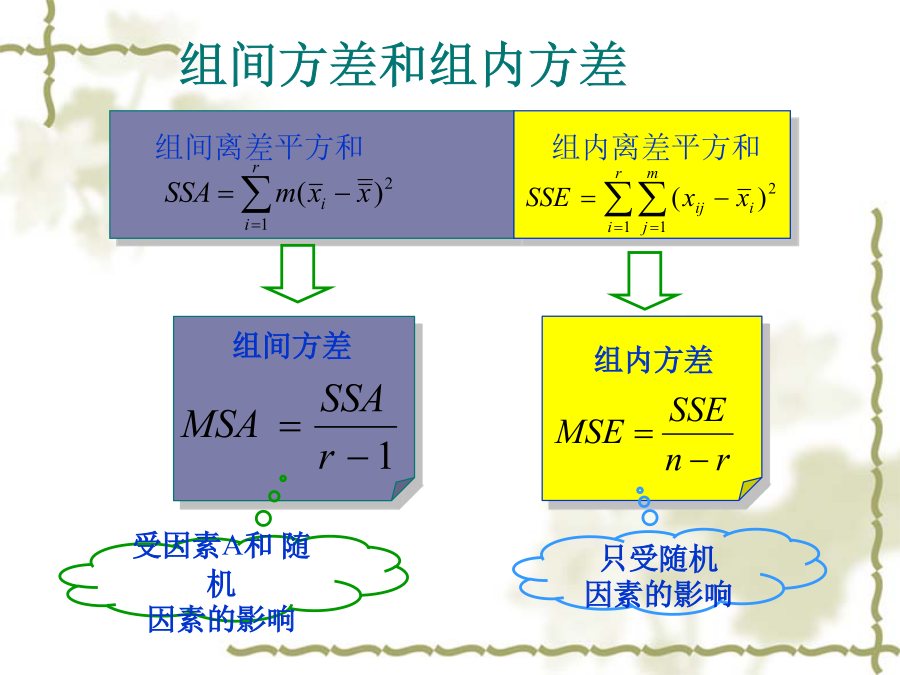
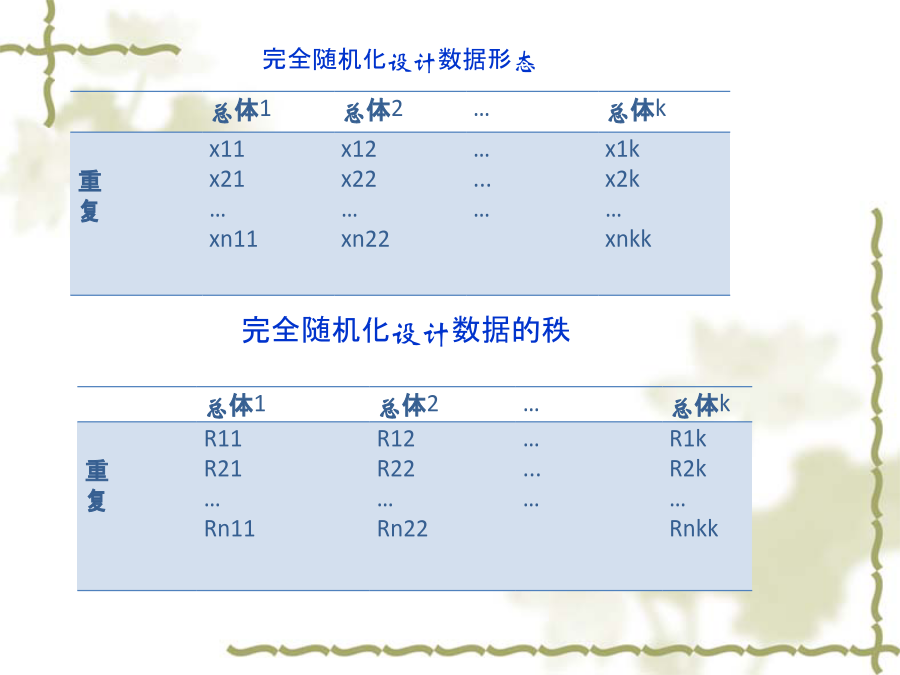
第四章多样本非参数检验在参数统计中，检验n个样本是否来自完全相同的总体，采用方差分析或F检验。
运用F检验的假定条件是：
1，样本是从服从正态分布的总体中独立抽
选的；
2，总体具有相同的方差；
3，数据的测量层次至少是定距尺度。
当被用来分析的数据不符合这些假定条件，或研究者不希望做这些假设，以便增加结论的普遍性时，不宜采用参数统计的方法，而必须用非参数方法。如果k（>2）个样本是按某种或者某些条件匹配的，那么k个样本称为相关的，否则为独立的。K个相关和独立样本的差别与两个相关和独立样本之间的差别类似。
多样本的问题是统计中最常见的一类问题。主要涉及如何检验n种不同方法、决策或试验条件（称为处理）所产生的结果是否一样等问题，可以使用Kruskal-Wallis秩和检验、卡方检验、正态记分检验、Jonkheere-Terpstra检验、CochranQ检验、Friedman检验等非参数检验方法。本章仅介绍其中的最常用、重要的检验方法。复习：方差分析的基本思想组间方差和组内方差多样本的非参数检验方法4.1Kruskal-Wallis检验4.1.1基本思路与检验步骤完全随机化设计数据形态
为检验零假设，我们需要构造一个检验统计量。方法是将所有数据按从小到大的顺序合并成一个单一的样本，其大小。将每一个观察值给出一个等级即评秩，秩为整数，从1到N。对于N个观察值来说，平均等级是对于含有个观察值的第j个样本来说，等级总和的期望值是，若以Rj表示第j个样本的实际等级总和，则就表示k个样本中第j个样本等级总和与其均值的偏差。
如果H0为真，所有样本数据混合排列成一个单一的随机样本，等级即秩次应该在k个样本之间均匀地分布，各组中Rj的平均值差别不大，即各样本实际的等级总和即秩次和Rj与期望等级总和之间的偏差应很小。Kruskal-Wallis检验定义的统计量就是建立在实际等级总和Rj与期望等级总和的偏差的基础之上的。它定义为H，计算公式为：严格地讲，

其中严格地讲，

其中H的一般计算公式在小样本的情况下，已知（n1,n2,n3)和显著性水平，Kruskal-Wallis检验统计量Ｈ的临界值可通过查表得到。
在大样本情况下，Ｈ服从。
参照方差分析的Ｆ统计量服从Ｆ(k-1,N-k).
检验步骤：
(1)建立假设

如果偏重于考察位置参数，则所建立的假设是：

注意：备择假设对于k>2时不存在单侧备择的配对，因为对于来说，有k!=k*(k-1)*…*3*2*1种不同的有序排列，不便于进行检验。检验步骤：
(1)建立假设

如果偏重于考察位置参数，则所建立的假设是：

注意：备择假设对于k>2时不存在单侧备择的配对，因为对于来说，有k!=k*(k-1)*…*3*2*1种不同的有序排列，不便于进行检验。（2）计算检验统计量H
（3）作出决策。
当数据支持H0，不能拒绝H0；
当数据不支持H0，拒绝H0。
Refernces:
Kruskal,W.H.andWallis,W.A.(1952).Useofranksinone-criterionvarianceanalysis.J.Amer.Statist.Assoc.,47,583-621.
4.1.2应用训练方式A解：（1）建立假设

（2）计算检验统计量

（3）作出决策
，数据在5%的显著性水平上不能拒绝H0，表明4种训练方式的有效性没有什么显著差异。存在打结数据，用H可以修正为：

这里，为结统计量，ｇ为结的个数。4.1.3练习4.2检验4.2.1基本思路与检验步骤(2)计算检验统计量

(3)作出决策
当时，数据在a水平上拒绝H0；
当时，数据在a水平上不能拒绝
H0。多样本卡方检验的两点注意4.2.2应用各类人员参加体育活动情况的人数
解：（1）提出假设
H0：收听体育广播兴趣不同不影响参加体育活动
H1：收听体育广播兴趣不同参加体育活动情况也不同
（2）计算检验统计量：

（3）作出决策

因为所以数据在5%的水平下拒绝H0，表明收听体育广播兴趣不同的人，参加体育活动的情况也不同。例2表中数据是由968个成人个案构成，根据他们的政党派别以及他们在1980年总体选举中的投票状况。解：首先根据公式计算期望次数如下：计算统计量：

统计量的临界值

结论：拒绝投票偏好与党派无关的零假设。4.2.3练习4.3Friedman检验Friedman检验是对k个样本是否来自同一总体的检验。k个样本是匹配的，可以由k个条件下同一组受试者构成，也可以将受试者分为n组，每组均有k个匹配的受试者，随机地将k个受试者置于k个条件下。在不同受试者匹配的样本中，应尽量使不同受试者的有关因素匹配即相似。
每一个样本代表了一个处理。在实际中，除了处理之外，往往还有别的因素起作用。比如在关于肥