
基片集成波导I.ppt

YY****。。








亲,该文档总共31页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

基片集成波导I.ppt
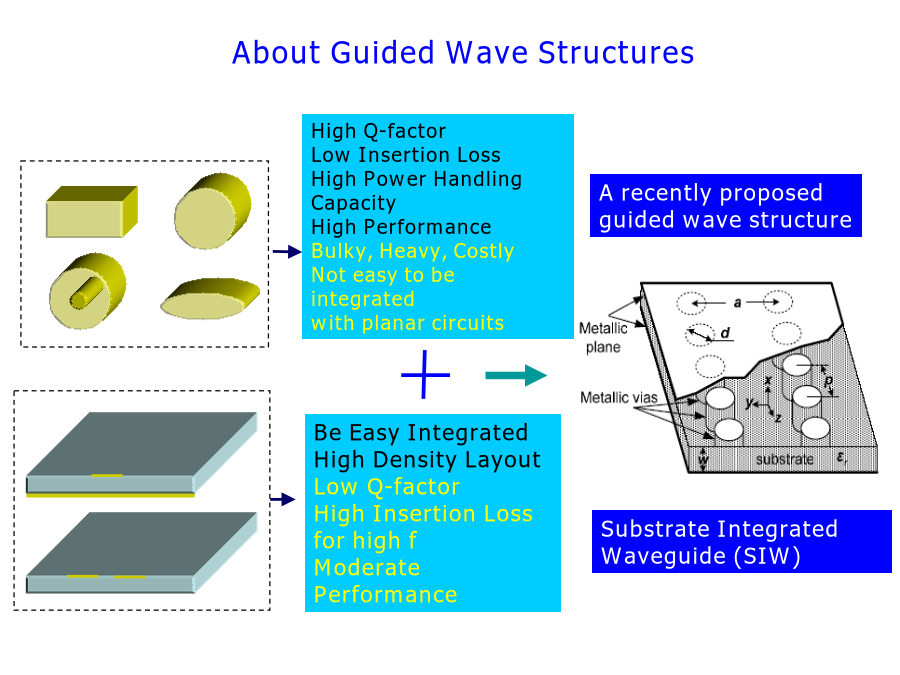
一基片集成波导的传播特性二基片集成波导的应用图1基片集成波导结构图一基片集成波导的传播特性1.基片集成波导结构的实现方法及其分类2.对基片集成波导与矩形波导等效的分析3.对基片集成波导结构的数值分析4.基片集成波导电磁传输特性AboutGuidedWaveStructures基片集成波导基片集成波导(SubstrateIntegratedWaveguide缩写为SIW):是一种在介质基片上采用印刷工艺实现的新型微波、毫米波导波结构。这种波导是一种平面传输线,同时它又具有与传统金属波导相似的传播特性,因而兼

第5讲基片集成波导-I.pptx
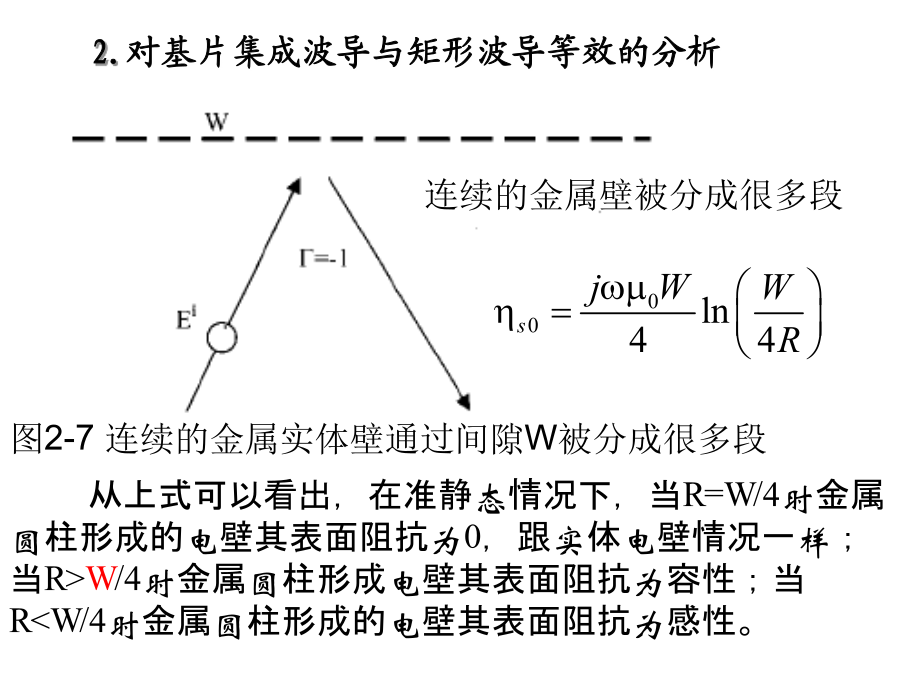
一基片集成波导的传播特性二基片集成波导的应用图1基片集成波导结构图一基片集成波导的传播特性1.基片集成波导结构的实现方法及其分类2.对基片集成波导与矩形波导等效的分析3.对基片集成波导结构的数值分析4.基片集成波导电磁传输特性AboutGuidedWaveStructures基片集成波导基片集成波导(SubstrateIntegratedWaveguide缩写为SIW):是一种在介质基片上采用印刷工艺实现的新型微波、毫米波导波结构。这种波导是一种平面传输线同时

基片集成波导.ppt
基片集成波导技术研究研究背景基片集成波导的概念半波基片集成波导(HMSIW)的概念CST仿真的主模场分布(8GHz),基片厚度为1mm,0.5mm处的电场分布国内外研究现状6、W.Hong等人提出了半波基片集成波导(HMSIW)的概念(2006.10),在此基础上已经有关于HMSIW耦合器报道(2007.3)。介电常数1,a=20mm,s=5mm,d=10mm,上图为普通波导,中间s/d=0.5时的场分布,下图为s=d时的场分布基片集成波导和微带传输线的转接形式基片集成波导和微带线插损测试Applicat

基片集成波导实现方法概述.docx
基片集成波导实现方法概述引言基片集成波导是集成光电子芯片中常见的一个元件,它能够实现光信号的传输、分配、调制等功能。近年来,由于光通信、光雷达、生物传感、光学计算等领域需要高速、高稳定性的光学器件,因此基片集成波导得到了广泛的应用。本文将着重介绍基片集成波导实现方法的概述。主体基片集成波导是指光波导被集成在硅基片或其他半导体基片上,具有微小尺寸、高集成度和高可靠性等优点。目前,实现基片集成波导的方法主要分为三种:染料增强光刻法、光电子光刻法和离子注入法。一、染料增强光刻法该方法是基于自然光刻技术发展而来,

基片集成波导弯曲结构的研究.docx
基片集成波导弯曲结构的研究随着现代光子学技术的发展,波导技术已经成为了光电子学领域中的重要研究方向。基片集成波导,作为一种先进的波导技术,已经得到了广泛应用。与传统波导相比,基片集成波导可以大大降低光学系统的体积、损耗和成本。同时,在波导中的光子互相作用、能量传递的距离和范围也更加灵活。因此,基片集成波导在光电子学领域的应用前景非常广阔。在基片集成波导的研究中,波导的形状和结构是非常重要的。其中,基片集成波导弯曲结构的研究尤为重要。弯曲波导可以将光线导向所需的方向,使得波导用途更加广泛。同时,弯曲波导也可
