北师版八年级中心对称-豆柴文库

北师版八年级中心对称.ppt

2024-11-26

10金币

669KB

25页

YY****。。

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共25页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

北师版八年级-中心对称.ppt

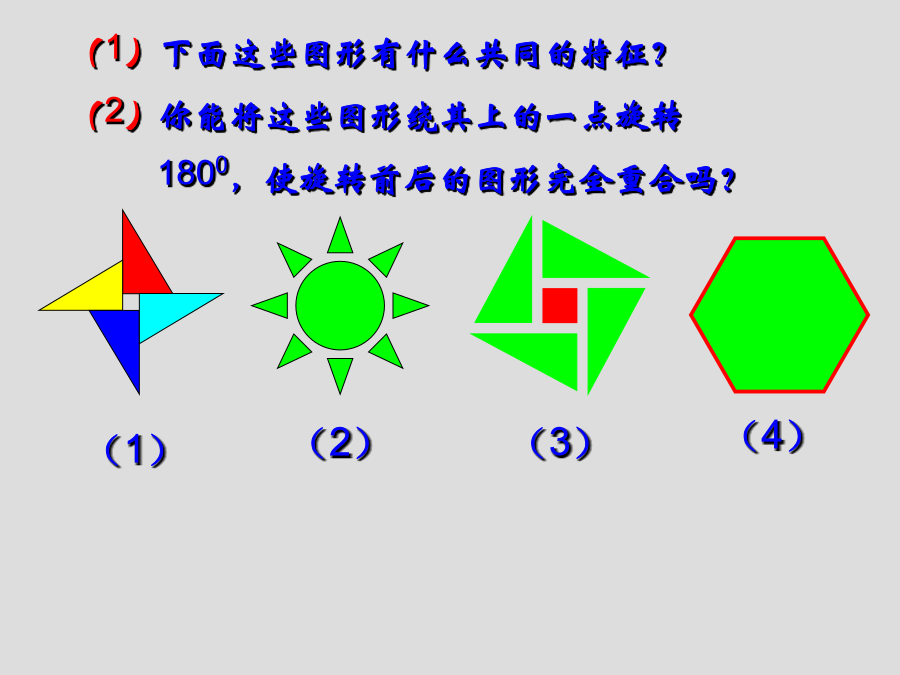
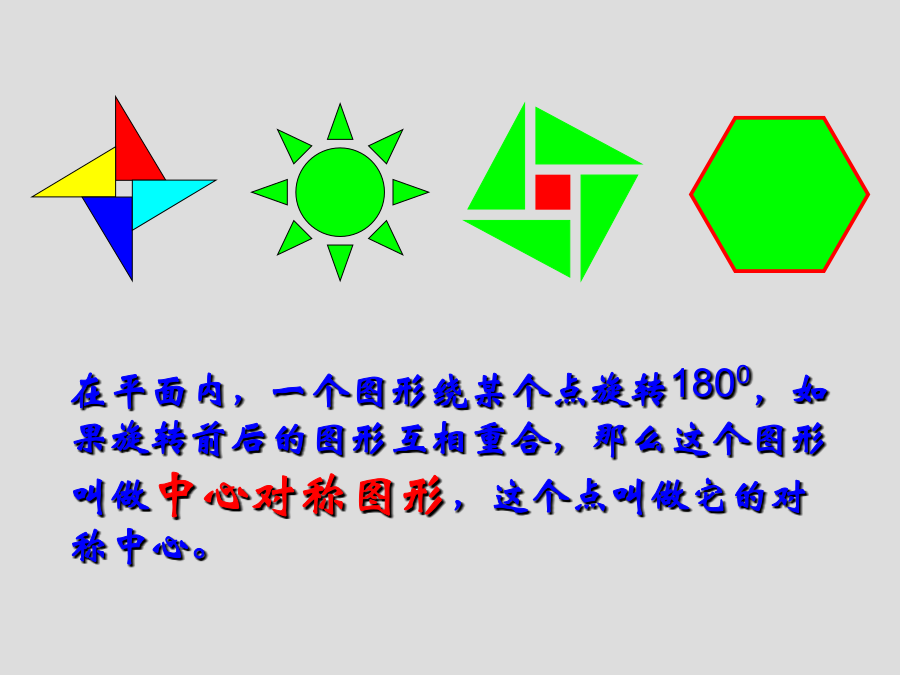
第三章3.3中心对称（1）A在平面内，一个图形绕某个点旋转1800，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。定理1关于中心对称的两个图形是全等形。O（3）在平行四边形、矩形、菱形、正方形、梯形、等腰梯形中，哪些图形是具有轴对称性？哪些图形是中心对称图形？议一议1、正方形是中心对称图形吗？正方形绕两条对角线的交点旋转多少度能与原来的图形重合？能由此验证正方形的一些特殊性质吗？正方形是中心对称图形吗？正方形绕两条对角线的交点旋转多少度能与原来的图形重合？能由此验证正方

北师版八年级中心对称.ppt

八年级数学上册《中心对称与中心对称图形》课件_北师大版.ppt

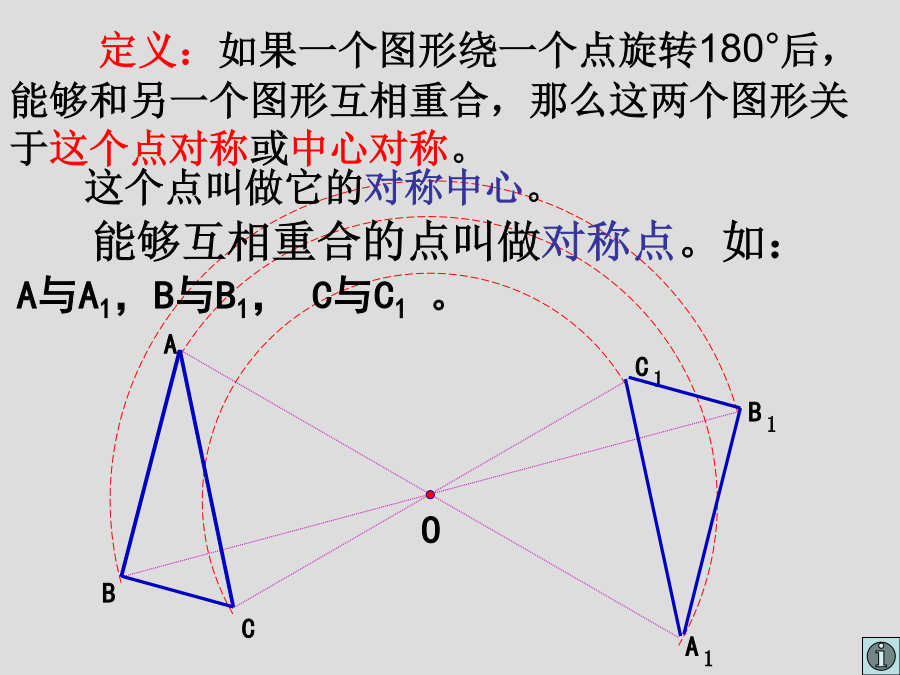
中心对称与中心对称图形观察下列各组图形,你能发现什么?观察下面两个图形，怎样变换可以使它们重合?把一个图形绕某一点旋转1800,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心,两个图形中的对应点叫做对称点.一个图形绕某一点旋转1800是一种特殊的旋转，因此成中心对称的两个图形具有图形旋转的一切性质.成中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分.想一想如图，2块同样的三角尺，它们是否关于某点成中心对称？若是，请确定它的对称中心.想

2024-07-17

390KB

中心对称课件2北师大版八年级.pptx

会计学观察下面的图形，你有什么发现？观察下面的两个图形你有什么发现?(1)把其中一个图案绕点O旋转180°,你有什么发现?概念并且由图知OA=OA`，同理有OB=OB`，OC=OC`。由此得到下面结论：（2）关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心平分．例1(2)如图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.3.已知四边形ABCD和点O,画四边形A’B’C’D’,使它与已知四边形关于点O对称。由已知条件，如果把其中一个图形绕着这个点旋转180

2024-09-23

1.5MB

北师大版八年级数学中心对称图形.doc

中心对称图形教学目标：(一)教学知识点1.了解中心对称图形及其基本性质.2.掌握平行四边形是中心对称图形.(二)能力训练要求1.经历观察、发现探索中心对称图形的有关概念和基本性质的过程积累一定的审美体验.2.了解中心对称图形及其基本性质掌握平行四边形是中心对称图形.(三)情感与价值观要求通过观察发现、动手操作、大胆猜想、自主探索、合作交流体验到成功的喜悦学习的乐趣并积累一定的审美体验。教学重点：中心对称图形的定义及其性质.教学难点：（1）、中心对称图形与轴对称图形的区别；（2）、利用中心对称图形的有关概

2023-05-27

568KB