
动目标检测器(MTD).ppt

YY****。。





亲,该文档总共49页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
动目标检测器(MTD).ppt
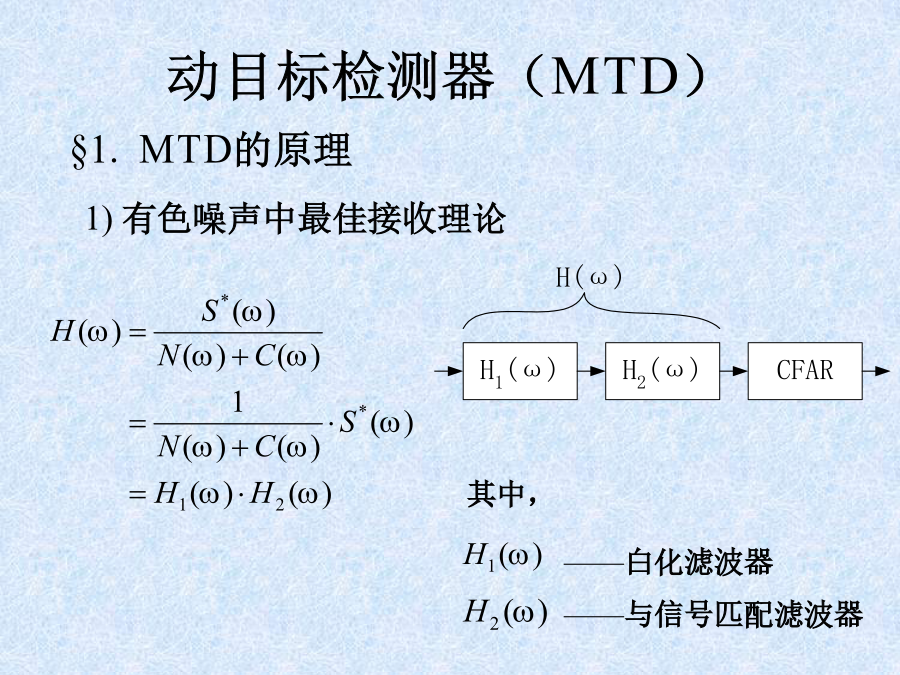
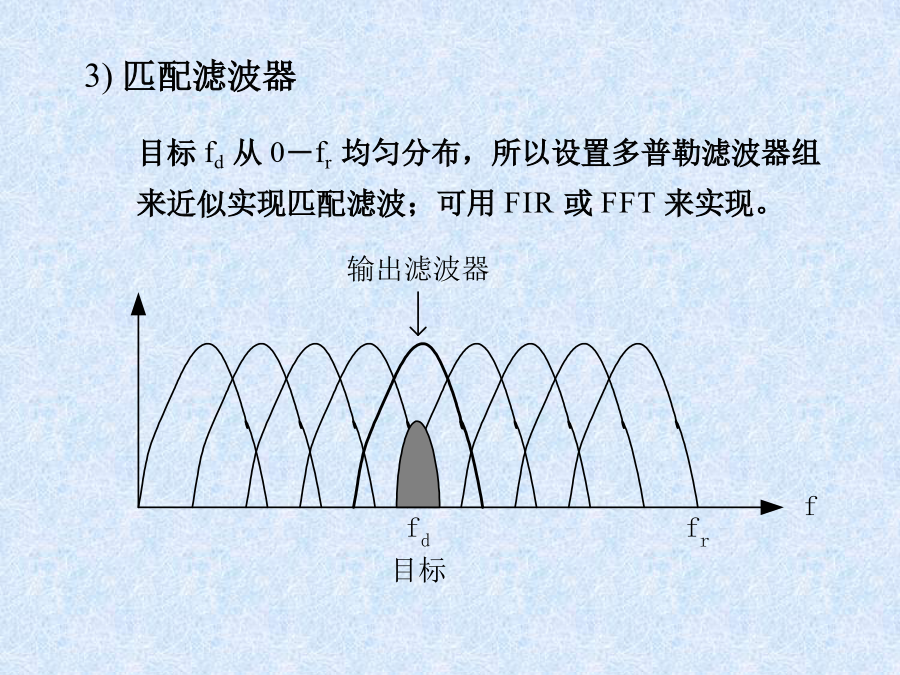
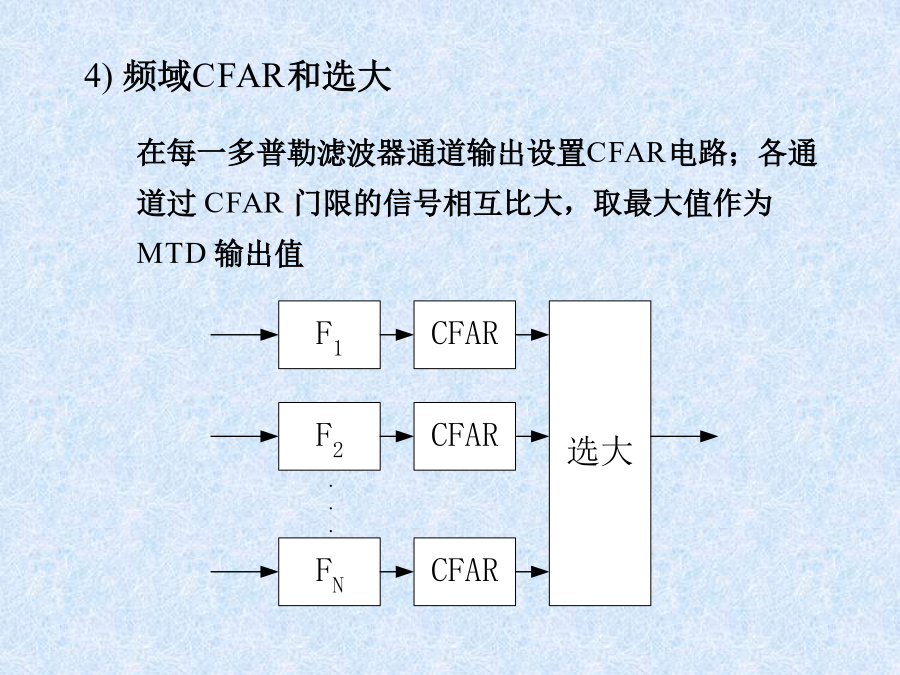
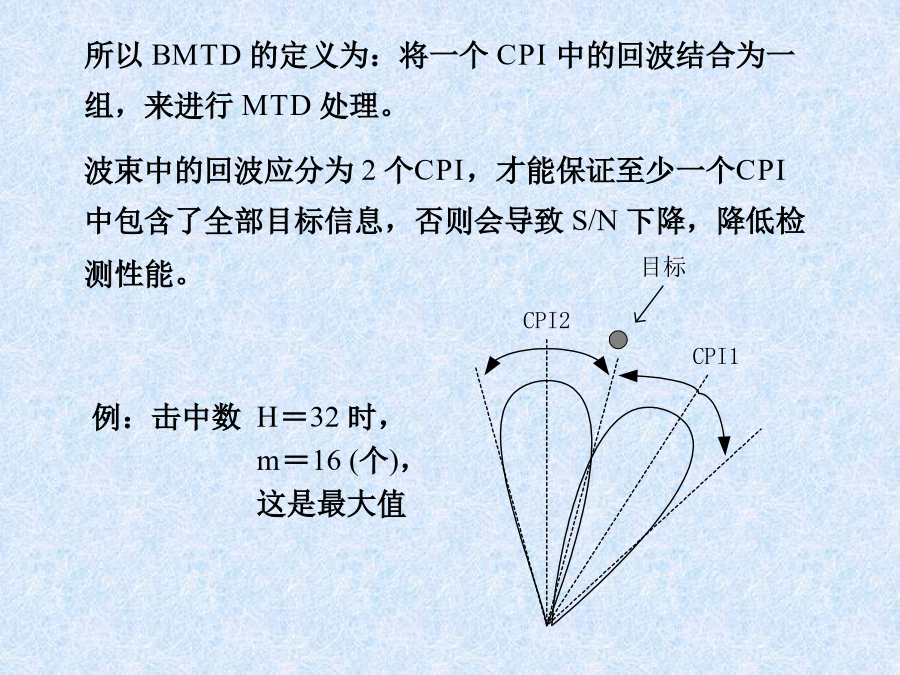
动目标检测器(MTD)2)白化滤波器的实现3)匹配滤波器4)频域CFAR和选大§2.成组处理MTD——BMTD所以BMTD的定义为:将一个CPI中的回波结合为一组,来进行MTD处理。波束中的回波应分为2个CPI,才能保证至少一个CPI中包含了全部目标信息,否则会导致S/N下降,降低检测性能。二.乒乓存储器:乒乓存储器容量:设:CPI=m距离间隔=nA/D字长=bbits例:CPI=64=mn=1024b=12bits则:Z=4×64×1024×12=384Kbytes三.多普勒滤波器组:2)多普勒滤波器组
动目标检测器(MTD).ppt
动目标检测器(MTD)2)白化滤波器的实现3)匹配滤波器4)频域CFAR和选大§2.成组处理MTD——BMTD所以BMTD的定义为:将一个CPI中的回波结合为一组,来进行MTD处理。波束中的回波应分为2个CPI,才能保证至少一个CPI中包含了全部目标信息,否则会导致S/N下降,降低检测性能。二.乒乓存储器:乒乓存储器容量:设:CPI=m距离间隔=nA/D字长=bbits例:CPI=64=mn=1024b=12bits则:Z=4×64×1024×12=384Kbytes三.多普勒滤波器组:2)多普勒滤波器组
动目标检测器(MTD)(PPT49页).ppt
动目标检测器(MTD)2)白化滤波器的实现3)匹配滤波器4)频域CFAR和选大§2.成组处理MTD——BMTD所以BMTD的定义为:将一个CPI中的回波结合为一组,来进行MTD处理。波束中的回波应分为2个CPI,才能保证至少一个CPI中包含了全部目标信息,否则会导致S/N下降,降低检测性能。二.乒乓存储器:乒乓存储器容量:设:CPI=m距离间隔=nA/D字长=bbits例:CPI=64=mn=1024b=12bits则:Z=4×64×1024×12=384Kbytes三.多普勒滤波器组:2)多普勒滤波器组

MTD微波交通检测器应用方案.pdf
MTD微波交通检测器应用方案国家智能交通系统工程技术研究中心北京中交国通智能交通系统

MTD微波交通检测器应用方案.pdf
MTD微波交通检测器应用方案国家智能交通系统工程技术研究中心北京中交国通智能交通系统
