优化理论基础.ppt

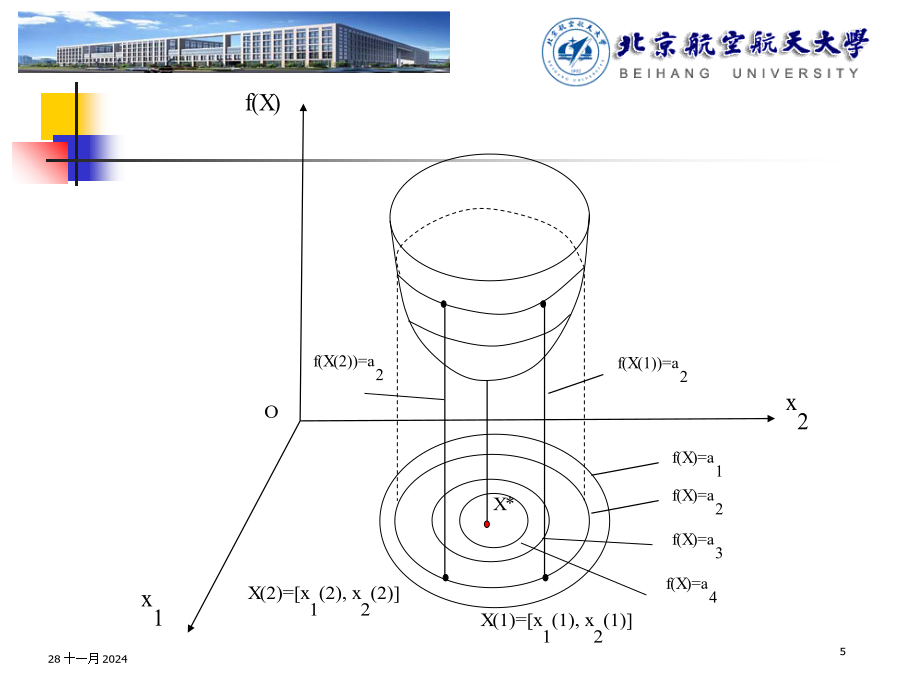
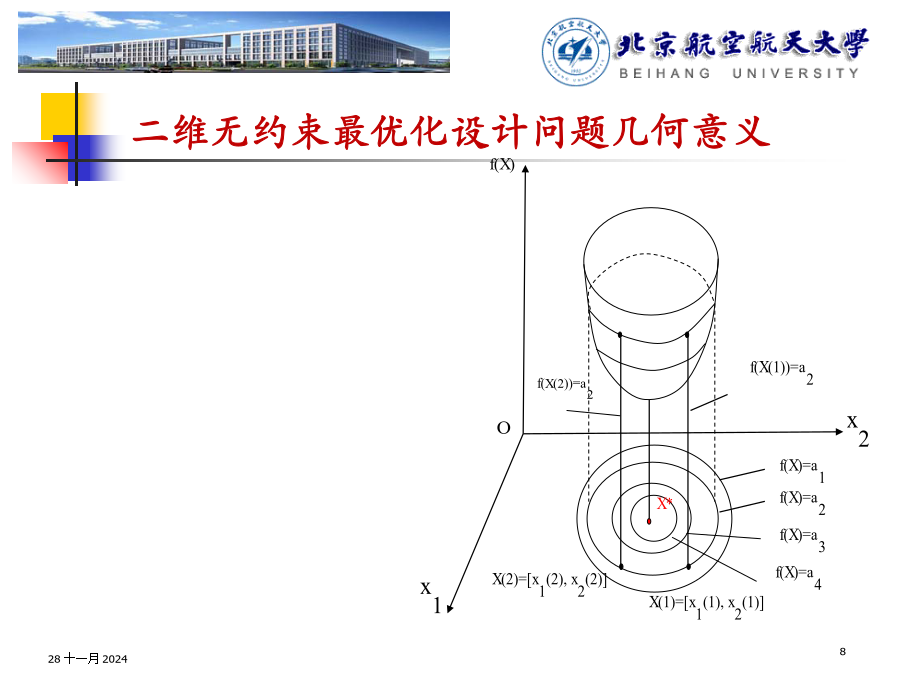
28十一月202428十一月202428十一月202428十一月202428十一月202428十一月202428十一月2024二维无约束最优化设计问题几何意义28十一月202428十一月202428十一月202428十一月202428十一月202428十一月202428十一月2024二维目标函数等值线形态分析28十一月2024二维优化问题进行几何描述几何意义上来说明约束最优解和无约束最优解28十一月20243-3局部最优解和全域最优解28十一月20243-4无约束目标函数的极值点存在条件28十一月2024仍以图中所示一元函数为例，由图可见，在x(1)与x(2)处的f’(x(1))与f’(x(2))均等于零，即函数在该两点处的切线与x轴平行。但使f’(x)＝0的点并不一定都是极值点。28十一月2024(2)极值点存在的充分条件函数的偏导数
偏导数是指在某坐标轴方向函数值的变化率

连续可微的n维函数f(X)=f(x1,x2,…,xn)，在点X(K)=[x1(K),x2(K),…,xn(K)]T的一阶偏导数表示为
，…，函数的梯度函数梯度的性质28十一月2024函数的赫森矩阵赫森矩阵正定和负定的判定设f(x)为定义在XDRn中的n元函数。向量X的分量x1,x2,…,xn，就是函数的自变量。

设x(k)为定义域内的—个点，且在该点有连续的n＋1阶偏导数，则在该点附近可用泰勒级数展开，如取到二次项28十一月202428十一月2024可简写为28十一月2024公式中只取到泰勒级数二次项，称为函数的二次近似表达式。

极值点存在的必要条件。n元函数在定义域内极值点X*存在的必要条件极值点存在充分条件亦即而当28十一月2024至此，完全不难自行归纳得出无约束目标函数极值点存在的充分必要条件和用数学分析作为工具对n维无约束优化问题寻求最优解。无约束目标函数的极值条件求三维函数的极值点。28十一月202428十一月2024设D为n维欧氏空间中设计点X的一个集合，若其中任意两点x(1)和x(2)的连线都在集合中，则称这种集合是n维欧氏空间的一个凸集。

二维函数的情况如图所示，其中图(a)为凸集，图(b)为非凸集28十一月202428十一月202428十一月2024用一元函数来说明函数的凸性。

如图所示，图(a)在x(1)、x(2)区间曲线为下凸的，图(b)的曲线是上凸的，它们的极值点(极小点或极大点)在区间内都是唯一的。

这样的函数称为具有凸性的函数，或称为单峰函数。28十一月202428十一月202428十一月2024三、凸函数的基本性质四、凸函数的判定判别法2：若函数f(X)在凸集D上存在二阶导数并且连续时，对f(X)在D上为凸函数的充分必要条件为：

对于任意的XD，f(X)的赫森矩阵H(X)处处是正半定矩阵。五、函数的凸性与局部极值及全域最优值之间的关系六约束极值点存在条件28十一月20242不等式约束问题的一阶最优性条件28十一月2024起作用约束下标集合用I表示K-T条件可阐述为：
如果X(k)是一个局部极小点，则该点的目标函数梯度f(X(k))可表示成该点诸约束面梯度gi(X(k))的如下线性组合：
gi(iI)在X(k)处可微；
gi(iI)在X(k)处连续；
gi(X(k))(iI)线性无关28十一月2024iI时，gi0，wi＝0
iI时，gi=0，对wi无限制
wig(X(k))=0，i=1，2，…，m称为互补松弛条件；
wi0，i=1，2，…，m，亦称拉格朗日乘子。
等式约束性问题的最优性条件几何意义是明显的：考虑一个约束的情况：

最优性条件即：3一般约束问题的一阶最优性条件如果x*是l.opt.,对每一个约束函数来说，只有当它是起作用约束时，才产生影响，如：K-T条件可阐述为：
如果X(k)是一个局部极小点，则该点的目标函数梯度f(X(k))可表示成该点诸约束面梯度gi(X(k))的如下线性组合：
f、gi(iI)在X(k)处可微
gi(iI)在X(k)处连续
hj(X(k))(j=1，2，…，l)在X(k)处连续可微28十一月202428十一月202428十一月202428十一月202428十一月202428十一月2024可能的K-T点出现在下列情况：
①两约束曲线的交点：g1与g2，g1与g3，g1与g4，g2与g3，g2与g4，g3与g4。
②目标函数与一条曲线相交的情况：g1，g2，g3，g4
对每一个情况求得满足K-T条件的点(x1，x2)T及乘子w1，w2，w3，w4，且wi≥0时，即为一个K-T点。下面举几个情况：g1与g2交点：x=(2,1)T∈S，I={1,2}则w3=w4=0解28十一月202428十一月2024七最优化设计的数值计算迭代方法迭代算